这里主要掌握两种遍历方法：递归法和迭代法

递归法：

1、确定递归函数的参数和返回值，这里参数就是节点和用于存放节点数值的vector。
2、确认终止条件，这里的终止条件是节点为空。
3、确定单层递归逻辑，根据前序、中序、后序遍历的顺序和特点进行取值。
 

前序遍历：（中左右）

class Solution {
public:
    void traversal(TreeNode* cur, vector<int>& vec) {
        if (cur == NULL) return;
        vec.push_back(cur->val);    // 中
        traversal(cur->left, vec);  // 左
        traversal(cur->right, vec); // 右
    }
    vector<int> preorderTraversal(TreeNode* root) {
        vector<int> result;
        traversal(root, result);
        return result;
    }
};

中序遍历：其preorderTraversal方法与前序遍历一样，只改变traversal中遍历的顺序（左中右）

void traversal(TreeNode* cur, vector<int>& vec) {
    if (cur == NULL) return;
    traversal(cur->left, vec);  // 左
    vec.push_back(cur->val);    // 中
    traversal(cur->right, vec); // 右
}

后序遍历：其也是只改变traversal中的遍历顺序 （左右中）

void traversal(TreeNode* cur, vector<int>& vec) {
    if (cur == NULL) return;
    traversal(cur->left, vec);  // 左
    traversal(cur->right, vec); // 右
    vec.push_back(cur->val);    // 中
}

迭代法：

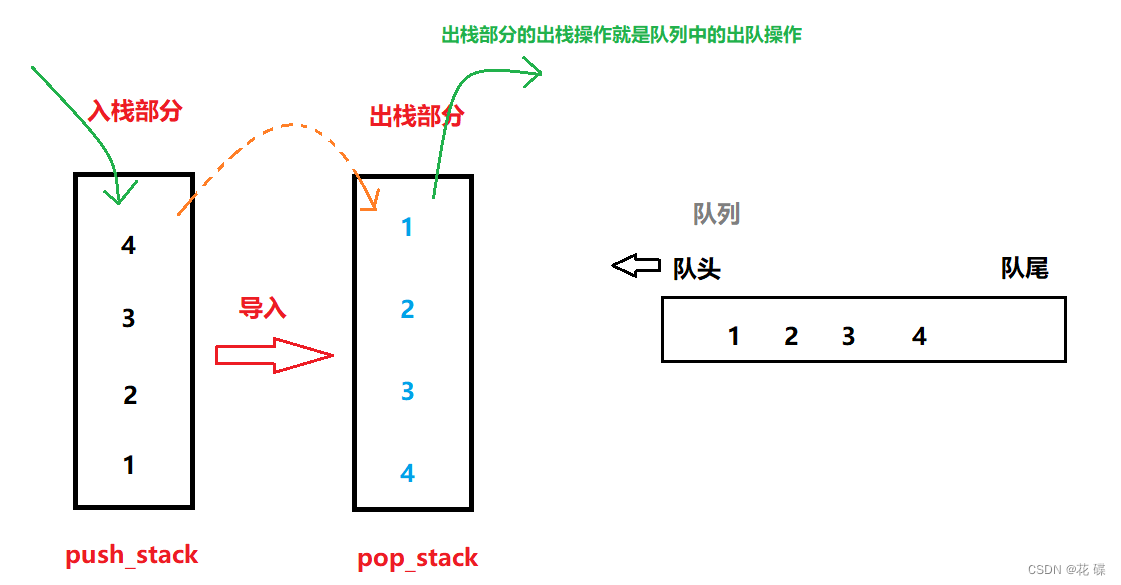
其实递归的本质就是对栈进行操作。所以迭代法就是对栈进行操作。

前序遍历：
先放入中间节点，
{再将栈入口的节点弹出，然后将弹出节点的右孩子加入栈，再加入弹出节点的左孩子}
{}中进行迭代。
为什么要先加入 右孩子，再加入左孩子？ 因为这样出栈的时候才是中左右的顺序。

vector<int> preorderTraversal(TreeNode* root)                //迭代法
     {
         stack<TreeNode*> Mystack;
         vector<int> Res;
         TreeNode* cur = root;  

         if(root == nullptr)
         return Res;        

         Mystack.push(cur);
         
         while(!Mystack.empty())
         {
            cur = Mystack.top(); 
            Mystack.pop();
            Res.push_back(cur->val);     
            if(cur->right != nullptr)
            Mystack.push(cur->right);
            if(cur->left != nullptr)
            Mystack.push(cur->left);
                         //弹出栈首元素 
         }

         return  Res;
     }

后序遍历：

可以套用前序遍历的方式，只不过后序遍历时，与前序遍历相反，先让左孩子入栈，再让右孩子入栈，如此以来获得（中右左）
但是后序本应该获得的为——左右中
故将 中右左 用reverse进行操作 得到左右中

vector<int> postorderTraversal(TreeNode* root)
    {
        stack<TreeNode*> mystack;
        vector<int> Res;
        TreeNode* cur = root;
        if(cur == nullptr)
        return Res;

        mystack.push(root);

        while(!mystack.empty())
        {
            cur = mystack.top();
            Res.push_back(cur->val);
            mystack.pop();

            if(cur->left != nullptr)
                mystack.push(cur->left);
            if(cur->right != nullptr)
                mystack.push(cur->right);
        }

        reverse(Res.begin(),Res.end());

        return Res;
    }

中序遍历：

中序遍历会稍微麻烦一些。
中序遍历是左中右，先访问的是二叉树顶部的节点，然后一层一层向下访问，直到到达树左面的最底部，再开始处理节点。

 vector<int> inorderTraversal(TreeNode* root) {
        vector<int> Res;
        stack<TreeNode*> Mystack;
        TreeNode* cur = root;

        if(root == nullptr)
            return Res;

        while(cur!= nullptr || !Mystack.empty())
        {
            if(cur != nullptr)
            {
                Mystack.push(cur);
                cur = cur->left;   //一直访问左子，直到左子为空
            }
            else   
            {
                cur = Mystack.top();  
                Mystack.pop();
                Res.push_back(cur->val);
                cur = cur->right;
            }   
       }
       return Res;
    }