一、归并排序
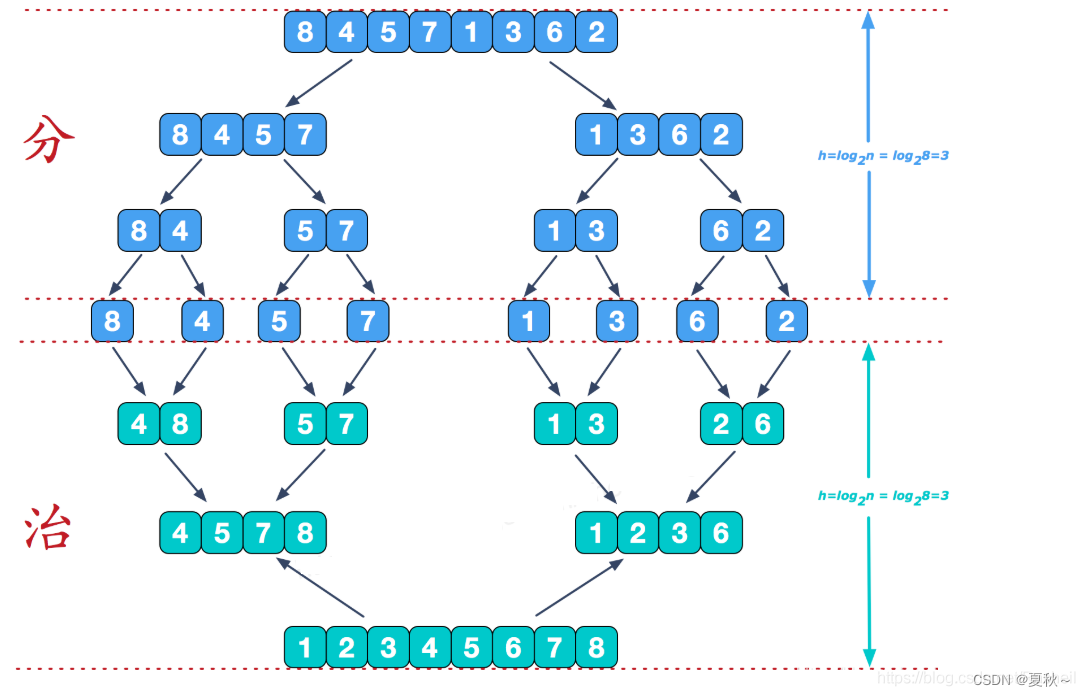
归并排序(Merge Sort)是一种基于分治思想的排序算法。它将待排序的数组分成两个长度相等的子数组,然后对这两个子数组分别进行归并排序,最后将两个排好序的子数组合并成一个有序的数组。
具体实现过程如下:
- 将待排序的数组分成两个长度相等的子数组;
- 对这两个子数组分别进行归并排序,即递归地调用归并排序函数;
- 将两个排好序的子数组合并成一个有序的数组。
二、归并排序的性质
归并排序具有以下性质:
-
稳定性:归并排序是一种稳定的排序算法,即相等元素的相对位置在排序前后不会发生改变。
-
时间复杂度:归并排序的时间复杂度为 O(nlogn),其中 n 表示待排序数组的长度。归并排序的时间复杂度比较稳定,不会因为数据的分布情况而产生较大的波动。
-
空间复杂度:归并排序的空间复杂度为 O(n),其中 n 表示待排序数组的长度。归并排序需要额外的空间来存储归并过程中的临时数组,因此空间复杂度比较高。
-
适用性:归并排序适用于所有数据类型,尤其适用于链表数据结构。在链表数据结构中,归并排序的空间复杂度可以优化为 O(1)。
-
可并行性:归并排序具有很好的可并行性,可以将待排序数组分成多个子数组,分别进行排序,最后将排序好的子数组合并成一个有序的数组。
三、归并排序的变种
归并排序有以下几种变种:
-
自然归并排序(Natural Merge Sort):自然归并排序是归并排序的一种变种,它可以对已经部分有序的数组进行排序,从而提高排序效率。自然归并排序的基本思想是将待排序数组中已经有序的子序列合并成一个更大的有序序列,然后再将这些有序序列合并成一个完整的有序序列。
-
两路归并排序(Two-Way Merge Sort):两路归并排序是归并排序的一种变种,它可以在原地进行排序,即不需要额外的空间来存储归并过程中的临时数组。两路归并排序的基本思想是将待排序数组分成两个子数组,然后将这两个子数组合并成一个有序的数组。
-
多路归并排序(Multi-Way Merge Sort):多路归并排序是归并排序的一种变种,它可以对多个有序数组进行排序,从而提高排序效率。多路归并排序的基本思想是将待排序数组分成多个子数组,然后将这些子数组合并成一个有序的数组。多路归并排序可以使用堆来实现,从而提高排序效率。
-
原地归并排序(In-Place Merge Sort):原地归并排序是归并排序的一种变种,它可以在原地进行排序,即不需要额外的空间来存储归并过程中的临时数组。原地归并排序的基本思想是将待排序数组分成多个子数组,然后将这些子数组合并成一个有序的数组。原地归并排序需要使用插入排序来对小数组进行排序,从而提高排序效率。
四、Java 实现
以下是 Java 实现归并排序的示例代码:
public class MergeSort {
public static void mergeSort(int[] arr, int left, int right) {
if (left >= right) {
return;
}
int mid = (left + right) / 2;
mergeSort(arr, left, mid);
mergeSort(arr, mid + 1, right);
merge(arr, left, mid, right);
}
public static void merge(int[] arr, int left, int mid, int right) {
int[] temp = new int[right - left + 1];
int i = left, j = mid + 1, k = 0;
while (i <= mid && j <= right) {
if (arr[i] <= arr[j]) {
temp[k++] = arr[i++];
} else {
temp[k++] = arr[j++];
}
}
while (i <= mid) {
temp[k++] = arr[i++];
}
while (j <= right) {
temp[k++] = arr[j++];
}
for (int p = 0; p < temp.length; p++) {
arr[left + p] = temp[p];
}
}
public static void main(String[] args) {
int[] arr = {5, 2, 8, 3, 6, 1, 7, 9, 4};
mergeSort(arr, 0, arr.length - 1);
for (int i = 0; i < arr.length; i++) {
System.out.print(arr[i] + " ");
}
}
}
在上述代码中,mergeSort 方法实现了归并排序的递归调用,merge 方法实现了归并排序的合并过程。在 main 方法中,我们可以调用 mergeSort 方法对数组进行排序。
五、归并排序的应用场景
归并排序适用于以下场景:
-
大规模数据的排序:归并排序的时间复杂度为 O(nlogn),其中 n 表示待排序数组的长度。因此,归并排序适用于大规模数据的排序。
-
外部排序:归并排序可以对外部存储器中的大规模数据进行排序,因为归并排序可以将待排序数据分成多个子数组,分别进行排序,最后将排序好的子数组合并成一个有序的数组。
-
链表排序:归并排序适用于链表数据结构的排序,因为链表数据结构不支持随机访问,而归并排序可以在链表数据结构中进行排序。
-
稳定排序:归并排序是一种稳定的排序算法,即相等元素的相对位置在排序前后不会发生改变。因此,如果需要保持相等元素的相对位置不变,可以使用归并排序进行排序。
六、归并排序在spring 中的应用
在 Spring 中,归并排序并不是一个常用的算法,因此在 Spring 框架中并没有直接使用归并排序的场景。但是,在 Spring 框架中有很多需要排序的场景,例如对 Bean 的属性进行排序、对集合进行排序等。在这些场景下,Spring 通常会使用 Java 中的排序方法,例如 Arrays.sort() 或 Collections.sort() 方法,这些方法都是使用快速排序或归并排序等高效的排序算法进行排序的。因此,可以说归并排序在 Spring 中的应用是间接的,通过 Java 中的排序方法进行应用的。