一句话总结:组合得次序是否重要,是否可重复,决定了组合数量
一、什么是组合&排序
组合可以是现实的一切事物、例如 [衣服,鞋子,眼镜...] 等等,
也可以表示一组数字 [1, 2, 3, 4, 5] ,从个人的使用角度来说,更多的意义代表的是数字,因此下面都会以数字作为案例。
排序是组合的一部分,只是在数学中需要根据’次序‘来区分开称呼。
二、组合&排序与次序的关系
组合与排序的叫法在数学中是有区分的,组合指的是不强调次序,而排序则强调次序。
例如有一组由 123这三个数字构成的数组,它的组合数量如下
[123, 132, 213, 231, 321, 312]假如现在要找出每组数组只要包含 123 就算符合要求,那么对于这个数组来说,里面的每一组都是符合,这种叫做不强调次序,组合数量会增多
假如要求每组数字必须包含 123 且顺序相同 对于这个数组来说只有第一组符合,
这种叫做强调次序,组合数量会减少
三、组合&排序与是否可重复的关系
组合除了考虑到次序问题,还要考虑到是否可重复的问题,
例如有一组由 123这三个数字构成的数组
[123, 132, 213, 231, 321, 312]仔细发现,这里的数组遵循着不可重复的特点,可以看到每组数字只能出现一次,
现在再来理解这类 123所构成的数组就清晰了
[
111, 112, 113
121, 122, 123,
131, 132, 133
211, 212, 213,
221, 222, 223,
231, 232, 233,
311, 312, 313,
321, 322, 323,
331, 332, 333
]这类的数组则遵循着可重复的特点。
我们还注意到,对于’可重复‘的组合明显比’不可重复‘的组合数量要多的多;
目前来讲,123这三个数组的组合数量看起来能接受,那如果是 1234567 的组合数量呢?
想必你也不想去手动算一遍,那可太麻烦了。
别急,现在你已经掌握了什么是’次序‘与’是否可重‘这两个重要概念,这已经足够了,下面是根据这两大特点对应的组合数量公式,公式的具体推导过程就不赘述了,可以参考网上资料;
三、排序(次序重要)
可重复
公式:
说明:n 代表组合内的个数,r 代表要提取的组合数量
举例:在 {1,2,3} 中这三个数字中取2个数字作为组合,代入公式得:

共有9组,不放心的话,我们也可以自己手写一遍:
[11, 12, 13, 21, 22, 23, 31, 32, 33]算了下,确实有9组。
不可重复
公式:
说明:! 符号表示递归乘积,例如 4! = 4x3x2x1
例子:在 {1,2,3} 中这三个数字中取2个数字作为组合,代入公式得:
 =
= 
共有6组
四、组合(次序不重要)
可重复
公式: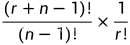
说明: 强调了次序不重要,因此要乘以它来进行降组合数量
强调了次序不重要,因此要乘以它来进行降组合数量
例子:在{1, 2, 3} 这三个数字中取2个数组作为组合,代入公式的:
 =
=  =
=  =
=  = 6
= 6
共有6组,不放心的话,我们也可以自己手写一遍:
[11, 12, 13, 22, 23, 33]算了下,确实有6组。
不可重复
公式:
例子:在{1, 2, 3} 这三个数字中取2个数组作为组合,代入公式的:
 =
=  =
= 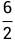 = 3
= 3
共有3组,不放心的话,我们也可以自己手写一遍:
[12, 13, 23]算了下,确实只有3组
注意:组合不强调次序,因此像 [21, 31, 32] 与上面是等价的,因此不计。
五、生活中的案例
彩票(不强调次序&不可重复)
玩过彩票的人都知道,只要你购买的号码出现在开奖结果里面时,就算中奖。
这里强调了次序不重要,每个数字都是独立的,也强调了不可重复性质。
沙拉搭配(不强调次序&可重复)
比如沙拉食物有{香蕉,西瓜,蔬菜,鸡蛋, 鸡胸肉}
假设现在你是消费用户,只能在这5种沙拉任选3样,每种食物都可以重复点,通过这种模式的组合,
强调次序不重要,但可重复的性质。
密码锁(强调次序&可重复)
行李箱密码锁就强调了次序的重要性,总不可能设置 123 时,输入个 321 还算对吧~
这里的可重复性质也是必要的,增加了密码的复杂度,即增加组合数量。
排名(强调次序&不可重复)
假设有5个人,其中任选3个作为123的排名,问有多少组合?
这里强调了次序重要,也强调了不可重复的性质。