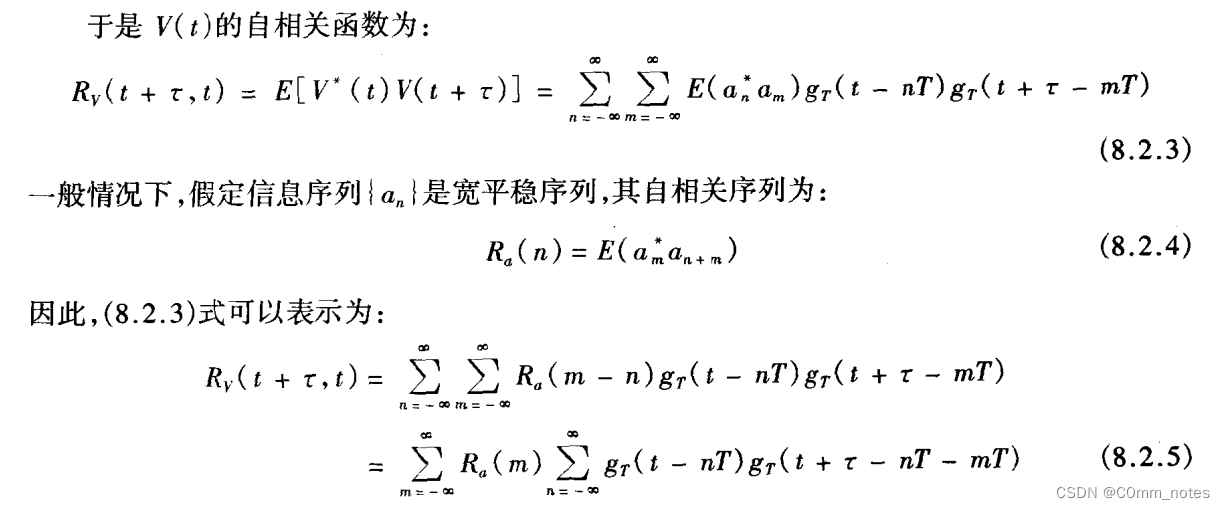封面图来源：
https://www.pexels.com/zh-cn/photo/210182/

编者按：

本文考虑了单程式共享汽车的定价问题，在考虑顾客需求网络效应以及实现影响的场景下，根据空间以及时间确定汽车租赁的单价以实现系统利润最大化。

1.引言

在过去的几十年中，共享交通系统已经成为城市内部交通的重要组成部分。现代共享交通系统较为为广泛的是单程式共享汽车租赁，顾客可以在某一站点取车，并在任意站点换车（不需要强制归还至起始站点）。在一般的共享出行系统中，定价优化被证明是一种有前景的增加利润的手段，但其面临着车辆供应有限以及顾客需求时空不平衡的挑战。

因此，本文在共享汽车系统中引入了基于起点的、利润最大化的定价问题。该问题在考虑供给侧网络效应以及实践影响的情况下，确定不同空间以及时间的汽车租赁单价。文章基于确定性网络流模型，将该问题表述为一个混合整数线性规划，并证明了它为NP-hard问题。

为了解决这一问题，提出了一种基于近似动态规划的时间分解方法，它考虑了未来利润与网络效应，并将其整合进价值函数近似中。我们基于意大利佛罗伦萨Share Now的数据进行案例研究。计算实验证明了在定价中考虑这种网络效应的好处，同时也展示了我们的值函数近似精确预测它们的能力

2.基于起点的共享出行系统差异化定价问题

2.1 问题描述

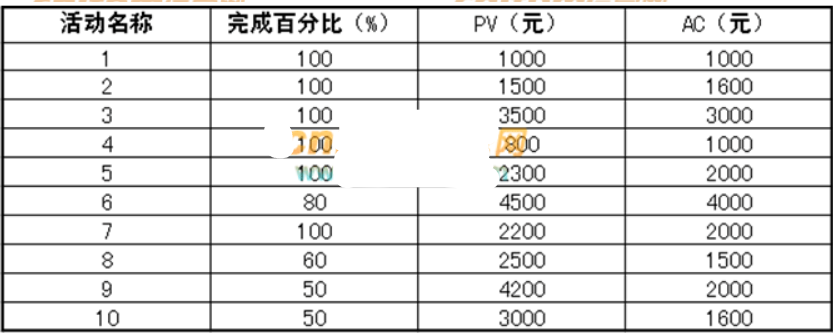
考虑一个单程式共享汽车服务提供商（SMS），它需要在给定的时段实现差异化定价。首先，SMS拥有站点集合 Z ∈ { 0 , 1 , . . . , Z } Z\in \{0,1,...,Z\} Z∈{0,1,...,Z}，时段集合 T ∈ { 0 , 1 , . . . , T } T\in\{0,1,...,T\} T∈{0,1,...,T}，单价集合 m ∈ M = { 0 , 1 , . . . , M } m\in M=\{0,1,...,M\} m∈M={0,1,...,M}。对于所有源于特定站点$i\in Z$、特定时段$t\in T$的租赁，不论其目的地在哪，均收取相同单价。现在，SMS的目标是设定不同的单价，使得共享汽车系统在给定的时间间隔内获得的利润最大化。该问题的对应解为优化后的定价表，如表1所示。

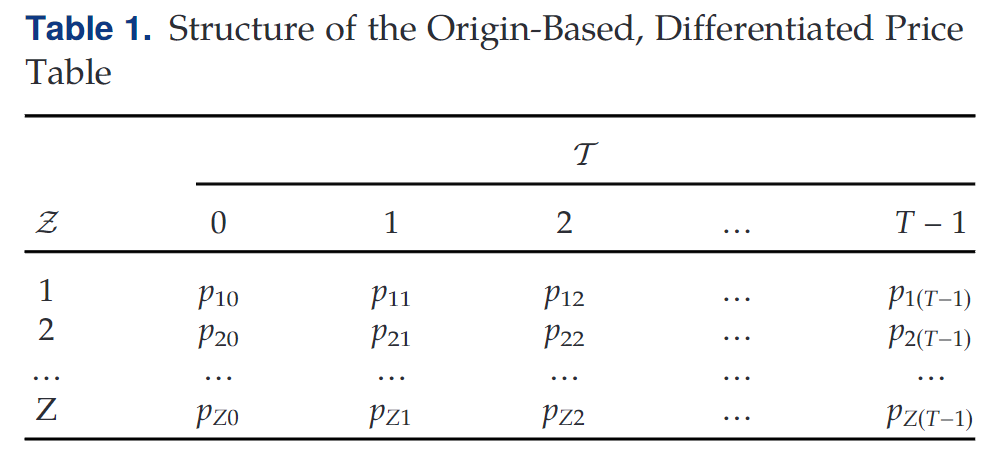
2.2 数学模型

本文建立了一个确定性的网络流模型以描述基于起点的差异化定价问题，该模型中流量的变化参考Figure 1中的时空网络。 模型中的各个弧度表示了共享汽车系统中车辆的移动以及站点中的可用车辆数。

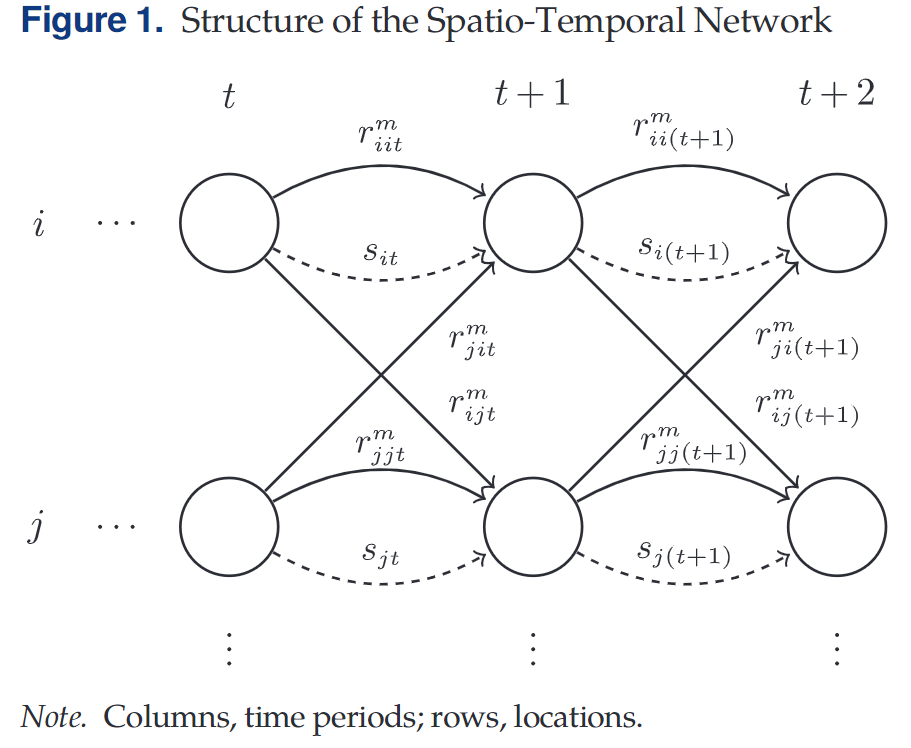
上图中包含了多个连续变量以表述系统中车辆的状态。$r_{ijt}^m$表示顾客在t时段以$p^m$的单价（元/分钟）从i站点租赁汽车前往j站点。而t时段的i站点剩余可用车辆被放置于i站点保持不动，用$S_{it}$表示。在t时段开始时i站点拥有的车辆用$a_{it}$表示。另外，模型中还包含了0-1变量。如价格决策变量$y_{it}^m=1$表示i站点在t时段的租赁单价为$p^m$。基于以上变量，建立共享汽车定价问题的混合整数线性规划模型如下：

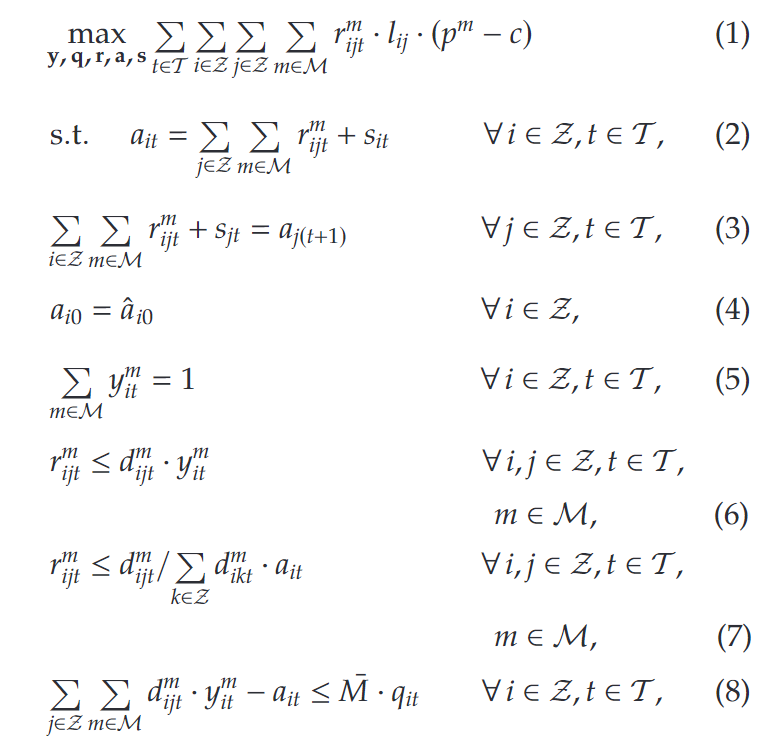
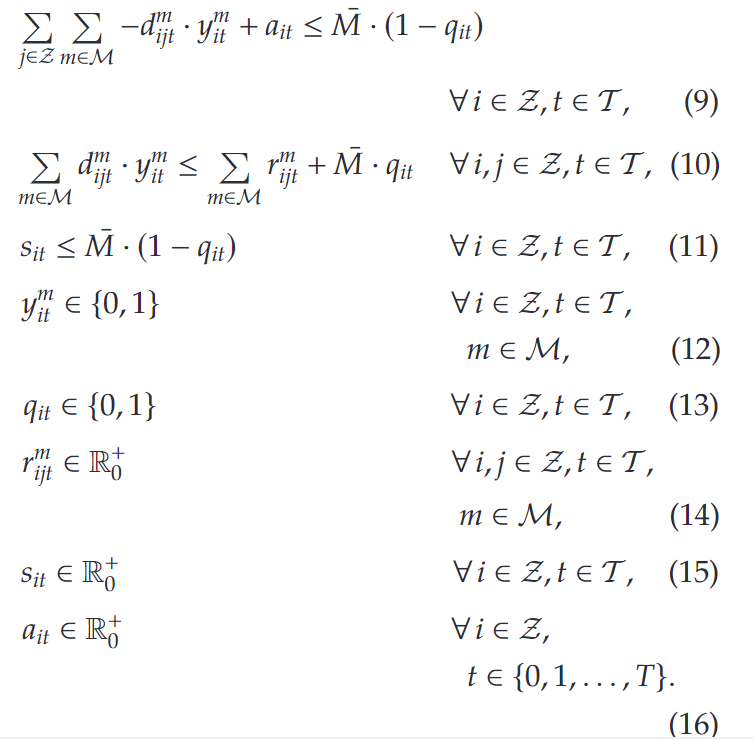
目标函数（1）为最大化系统所有时段的总贡献，计算方法是不同价格的租金收益减去可变成本。约束（2）、（3）为流量平衡约束，用于保证系统中车队规模不变。约束（4）设定了每个站点的初始车辆数目。约束（5）保证每个站点的每个时段只能选择一个租赁单价。约束（6）、（7）定义了顾客租赁的上限，这个限制取决于顾客需求以及车辆供应的的限制。约束（8）-（11）用于保证顾客租赁的下限，同时也保证当$p_{it}=p^m$时，租金$r_{it}^m=min(a_{it},{\sum }_{j\in Z}{d}_{ijt}^m)$.

3.数值实验​

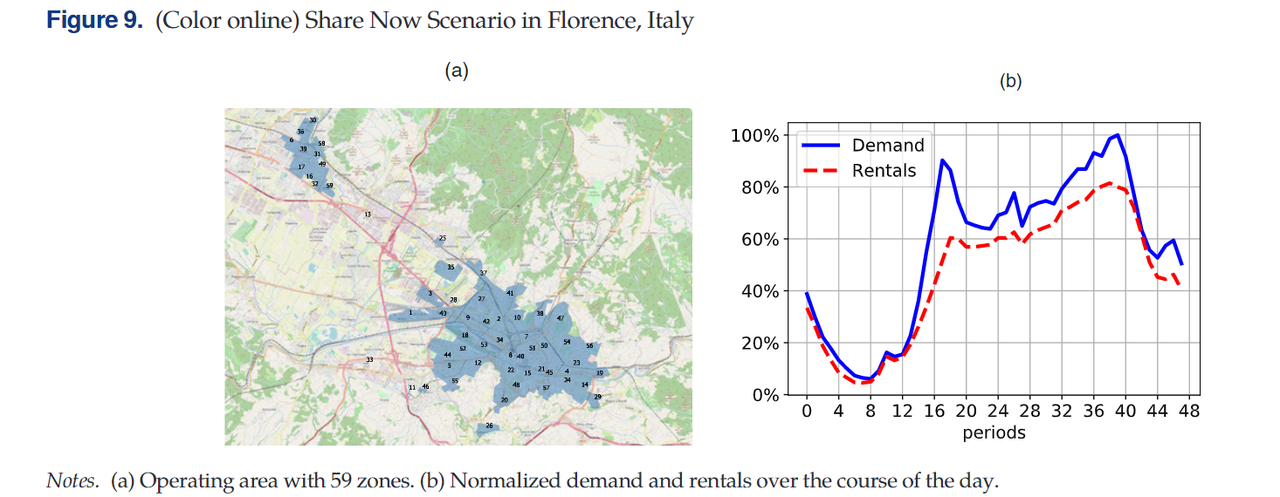
本节考虑了一个现实世界的场景，该场景反映了意大利佛罗伦萨的Share Now公司工作日期间基于起点的差异化定价案例。Share Now公司在佛罗伦萨的运营范围分为59个区域，如下图所示。同时，我们也可以观察到该公司在一天中48个时段的标准化需求$（d_t/max(d_t)$。很显然，在白天顾客需求和实际的租赁之间有较大的差距，而在夜晚顾客需求与实际租赁差别不大。这可以解释为白天顾客需求大、车辆供给紧张，因此车辆的可得性较低，而夜晚顾客需求小、空闲车辆更多，因此车辆可得性高。

3.1 算法参数的影响

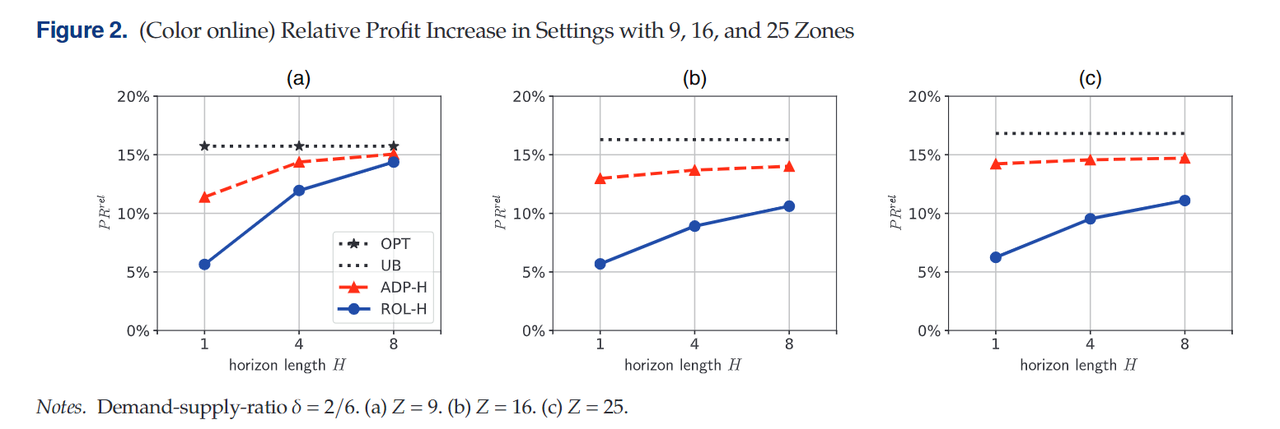
图2显示了不同站点数场景下四种策略算法的表现，包括OPT、UB、ADP-H以及ROL-H。对于ROL-H算法而言，当算法的horizon=1时，系统收益提升为10%左右，并且随着horizon的增加，算法提升的收益比例也在增加。图2的（a）中，共享汽车系统区域设置为9，改变ADP-H算法horizon的长度，分布设定为1、4、8，结果显示，利润的提升比例从11.4%增加到15.1%。与之相似，将系统的区域数目从9变化至16或者25，算法对系统的收益随horizon增加而增加。

3.2 网络时空效应价值函数

为了进一步描述时空网络效应对于系统的影响，我们对不同时间不同区域进行了参数评估，并将其整合进算法的运行中。首先价值函数的逼近公式如下：

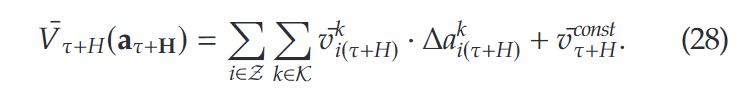
为了更好的分析具体某一区域的价值，定义价值函数如下：

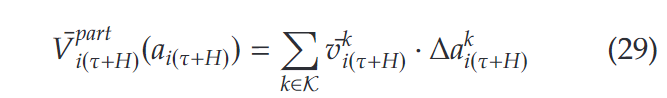
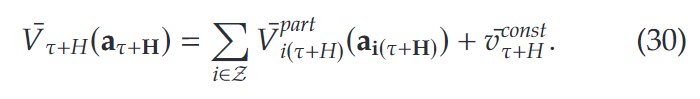
在以上公式的基础上，我们还需要结合table 4的参数估计，通过对不同时段以及不同区域的参数设定不同的数值，以表现网络时空效应的价值。具体的$v_{i(\tau +H)}^k$以及$v_{i(\tau +H)}^{const}$数值见table 4，不同时段的参数变化趋势见Figure 4、5.

$v_{i(\tau +H)}^k$

3.3 随机需求的影响

为了分析结果的鲁棒性，增加了对于随机需求场景的评估。具体而言，对于需求变量$D_{ijt}$，将其设定为随机扰动系数与标准需求相乘，扰动系统的标准差$\sigma \in 0,0.1,0.2,0.3,0.4$，公式如下：

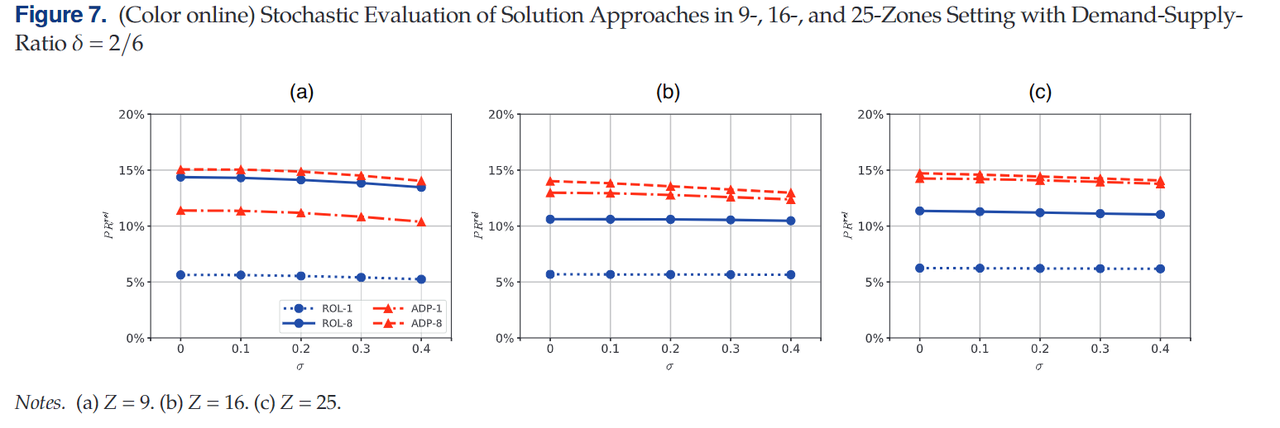
Figure 7展示了不同区域数场景下，不同标准差变化情形下4个算法的表现，包括ROL-1、ROL-8、ADP-1以及ADP-8。总的来说，本文提出的定价方法对于需求随机性变化是稳健的。然而，随着随机性的增加，所以算法利润的增长都有小幅下降的趋势。尽管如此，与无随机性情境相比，这些算法利润增长的下降最多为2个百分点，并且不同算法随随机性变化的变化均不相同，因此可认为本文提出的方法均比基准方法表现优秀。

4.总结与展望

在Share Now案例的支持下，本文分析了基于起点的共享出行差异化定价问题，在充分考虑共享汽车系统空间与时间差异的情况下，设定时空租车价格以实现利润最大化。数值实验显示，我们的定价方法在不同区域数目、需求模式下均比标准模式表现优秀——与单价不变的模式相比，我们的定价策略可提升15%的总利润；与不考虑网络效应的短视启发式策略相比，我们的定价策略提升10%的总利润。
在本文工作的基础上，未来研究方向可以进一步发展。首先，汽车供应商车队通常由不同的车辆类型组成，可以将模型从单一商品流扩展至多商品流问题表示。其次，尽管本文的方法被证明在非随机环境中是稳健的，但随机优化模型需要进一步改进。

参考文献：

Differentiated Pricing of Shared Mobility Systems Considering Network Effects. Matthias Soppert, Claudius Steinhardt, Christian Müller, and Jochen Gönsch. Transportation Science 2022 56:5, 1279-1303