目录
一.一维前缀
二.二维前缀和
三.一维差分
四.二维差分
一.一维前缀
1.前缀的作用
前缀用于在求一部分区间的和,比方说有一组数据a1,a2,a3,a4,我们想知道从第一个元素一直相加到最后一个元素的和或者是从第二个元素加到第三个元素,这种情况下就能使用前缀和了。
2.前缀和的思路
通常我们要求前缀和的时候题目会给出原始数组,我们需要另一个数组来记录每一个位置的前缀和,我们的前缀和数组记录从开头到当前位置的所有数据的和,用于后续的处理。这里用1,2,3,4,5,6,举例子,前缀和数组和原数组的对应关系如图,前缀和中一开始的0是为了处理求0个元素的前缀和。当我们要求部分区间的和的时候。我们直接用区间末的前缀和数据减去区间起始位置的前缀和就能求出这段范围的前缀和。因为我们前缀和数组内部存放的是从头到当前位置(原数组内)的数据和当我们做差的时候会将范围外的部分剪掉,这样留下的就是从范围起始位置到结束位置的前缀和了。这样求和的时间复杂度降为o(1)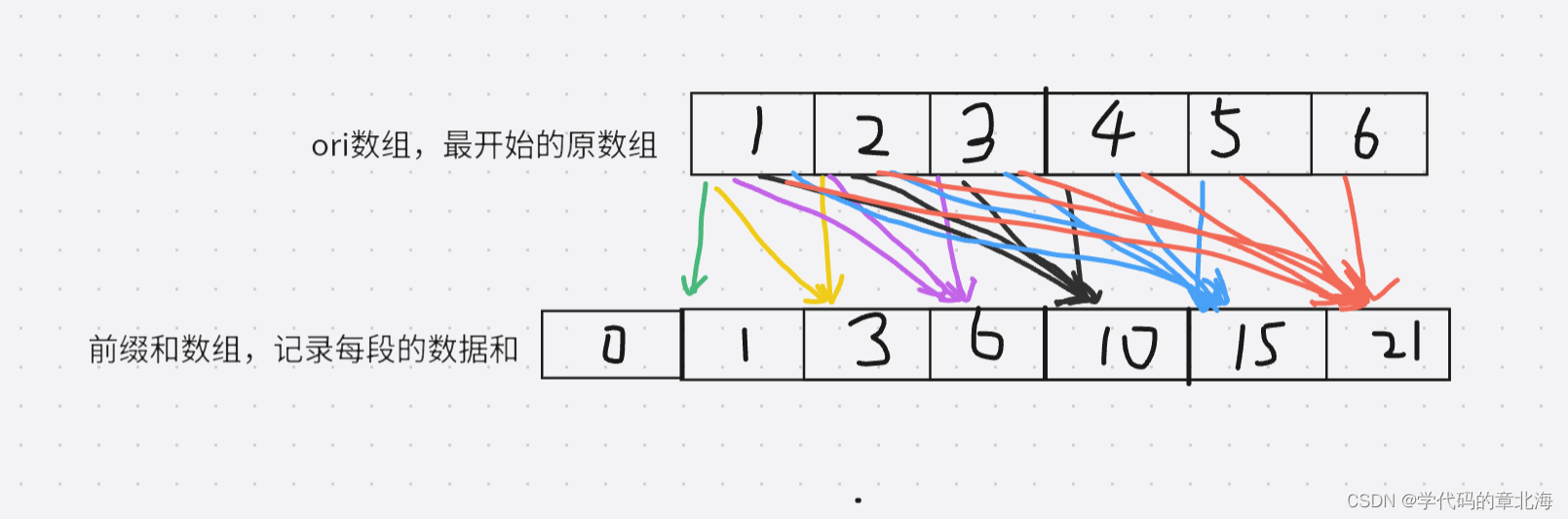
3.代码实现
//一维前缀和
const int N = 100010;
int s[N];
int main()
{
int n, m, l, r;
cin >> n >> m;
for (int i = 0; i < n; i++)
{
cin >> s[i + 1]; //把第一个位置空出来这样就不用再单独处理第0个元素的问题,同时和和让数组下标和题目要求相符
s[i + 1] = s[i] + s[i + 1]; //在输入的过程直接将前缀和计算出来(其实就是dp数组)
}
while (m--)
{
cin >> l >> r;
cout << s[r] - s[l - 1] << endl; // 从头加到位置r的前缀和减去从头加到l左边第一个位置的前缀和就是从l加到r的和,因为我们要去掉范围外的值,所以要减去l上一个位置的前缀和
}
return 0;
}二.二维前缀和
1.二维前缀和的作用:
在一维前缀和的基础上增加一维,原先的前缀和是从左向右计算,二维前缀和是从左上角向右上角计算的矩阵,这时候求的区间和是一个矩阵范围的区间和。
2.二维前缀和一维前缀和的大体思路是一样的。也需要构建前缀和数组来保存不同阶段的数据和。构建的前缀矩阵多表示一行一列,来对应求第0行或者第0列的情况。这个前缀矩阵保存的值就是从左上角第一个点到不同位置范围的和的值。所以我们需要首先计算出从最左上角到当前位置的前缀和,并用这个值形成前缀数组。
原数组和前缀和数组对应关系如图。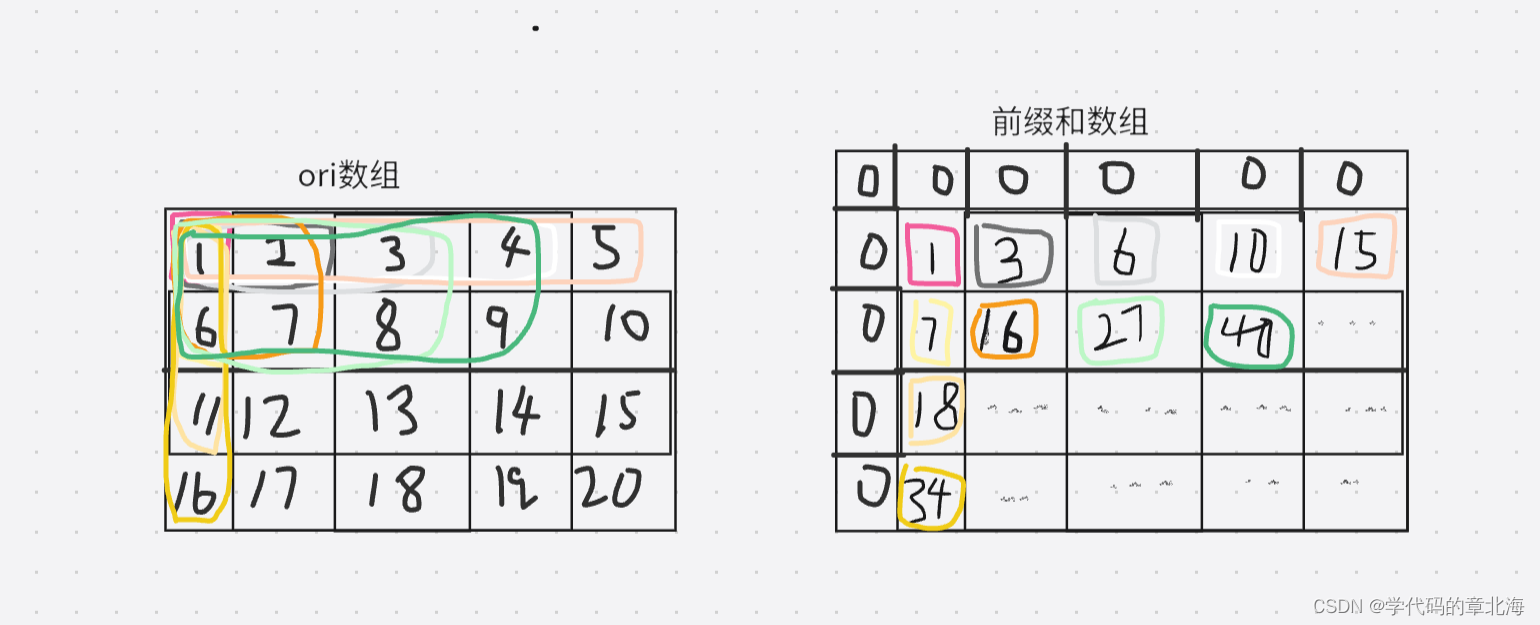
由一维前缀和我们可以知道范围末的前缀和减去范围和就是所求范围的值。二维也是同样的道理。我们取随机位置为例,在计算当前前缀和的时候,首先我们需要加上当前位置在原数组的值。然后再将上之前已经计算过的前缀和,由图中的对应关系我们可以明显看出,之前计算过的前缀和应该是在前缀和数组当前位置的左边和上边。同时我们也能发现,加上左边和上边的前缀和后,在原数组中当前位置左上角的矩阵会被重复计算两次。所以我们要减下去。这个重复计算的矩阵本身也是个前缀和,对应的就是前缀和数组中当前位置左上角的值。所以前缀和形成的过程如图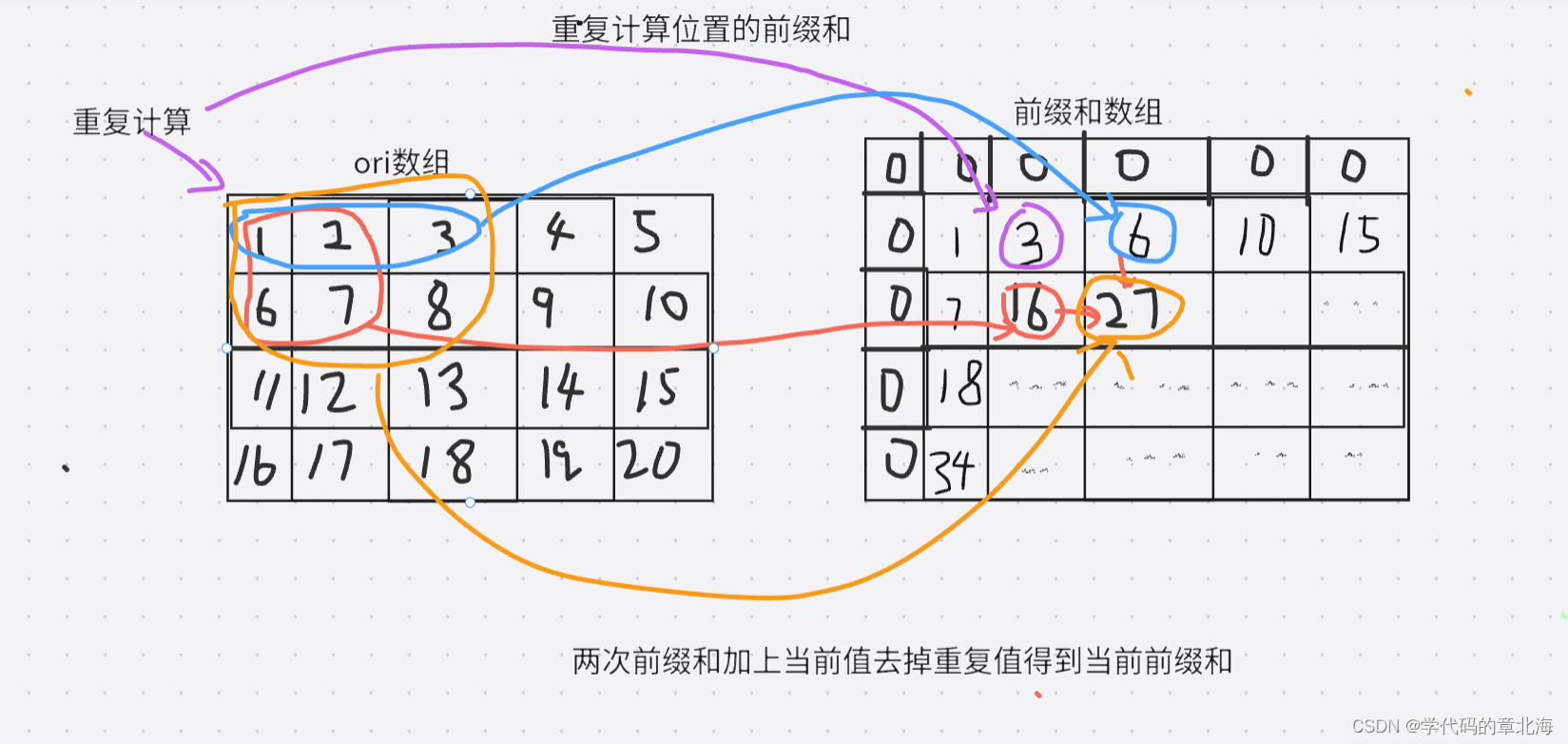
3.代码实现
二位前缀和
const int N = 1010;
int s[N][N];
int main()
{
int n, m, x1, y1, x2, y2, q;
cin >> n >> m >> q;
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= m; j++)
{
cin >> s[i][j];
s[i][j] = s[i - 1][j] + s[i][j - 1] + s[i][j] - s[i - 1][j - 1]; //插入的时候直接用新加入的值加上左边和上边的前缀和最后去掉重复计算的部分也就是左上角的前缀和
}
}
while (q--)
{
cin >> x1 >> y1 >> x2 >> y2;
cout << s[x2][y2] + s[x1 - 1][y1 - 1] - s[x2][y1 - 1] - s[x1 - 1][y2] << endl;//最后用要求的右下角的前缀和(这里的前缀和是大于我们要求的范围的)减去每个范围外的右下角的前缀和
//就是减去x2行的左边范围外的第一个值和y2列上边范围的第一个值,最后减去重复的部分,也就是两端范围减重复的部分
}
return 0;
}
三.一维差分
1.一维差分的作用:
当我们拿到一个数组并想对数组一定范围内的每个数据进行加减时候可以用到差分的思想。差分的本质就是前缀和的逆向操作,通过前缀和的数组反向求出原来的数组就是差分。我们通过求出原来的数组并对原来数组的某个数据进行加减,操作后再求前缀和数组就能拿在一定范围对每个数据进行加减后的前缀和数组。(因为前缀和数组是由原数组依次叠加出来的,所以原数组修改一个值对应的就是前缀和数组里当前位置以后的所有值全部受影响)这样就能让原来对前缀和数组o(n)的操作变成对原数组o(1)的操作
2.一维差分的思路:
我们把拿到的数组当成前缀和数组,这样对当前这个数组的范围内相加减就能转换成对差分数组的操作。于是我们要先构建出差分数组。因为我们知道差分数组是前缀和的逆向操作,所以我们在插入的时候可以通过计算两个相邻前缀和的差值计算出当前差分数组的值。再根据要修改的范围对差分数组进行修改。最后对修改后的差分数组求前缀和就能得到修改后的前缀和数组。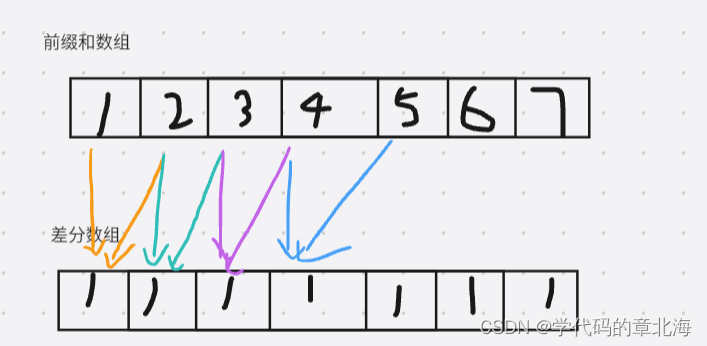
前缀和数组和差分数组的构造关系如图,加入我们想在前缀和数组从4到6每个数据都加上2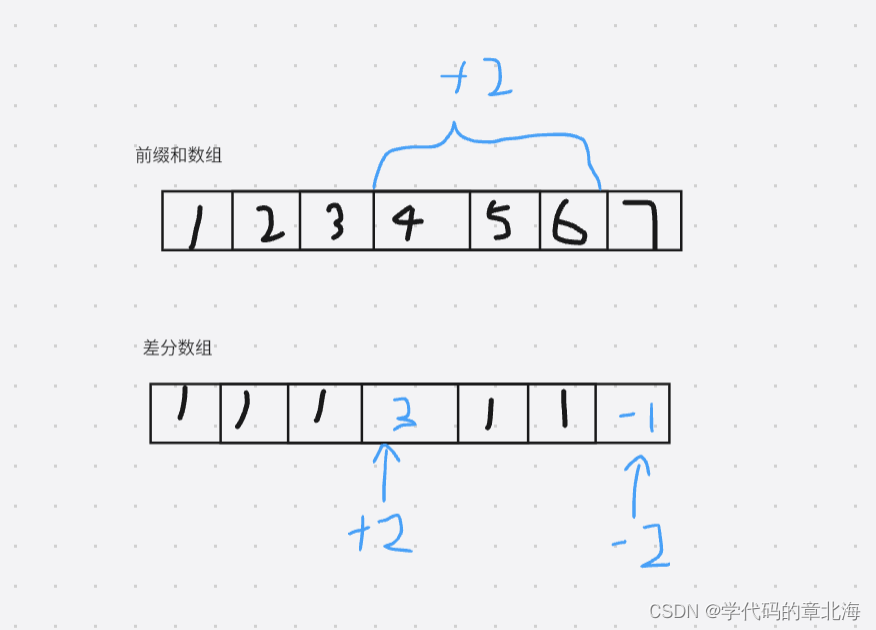
我们在差分数组内对数据进行修改最后在合成新的前缀和数组,就能得到我们想要的操作。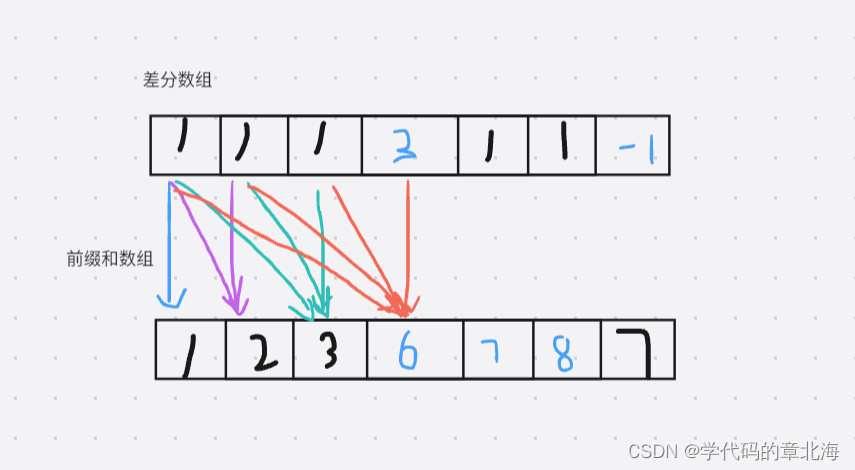
四.二维差分
1.二维差分的作用:
可以类比二维前缀和的做法。二维差分就是二维前缀和的逆向运算,通过构造出二维差分数组,将对前缀和的范围区间操作转换成对差分数组的一维操作。
2.二维差分的思路:
我们拿到给定的矩阵后将其作为二维前缀和数组。我们先要反向操作求出二维差分数组。通过二维前缀和我们已经知道前缀和数组和差分数组的对应关系了,这里就不在画了。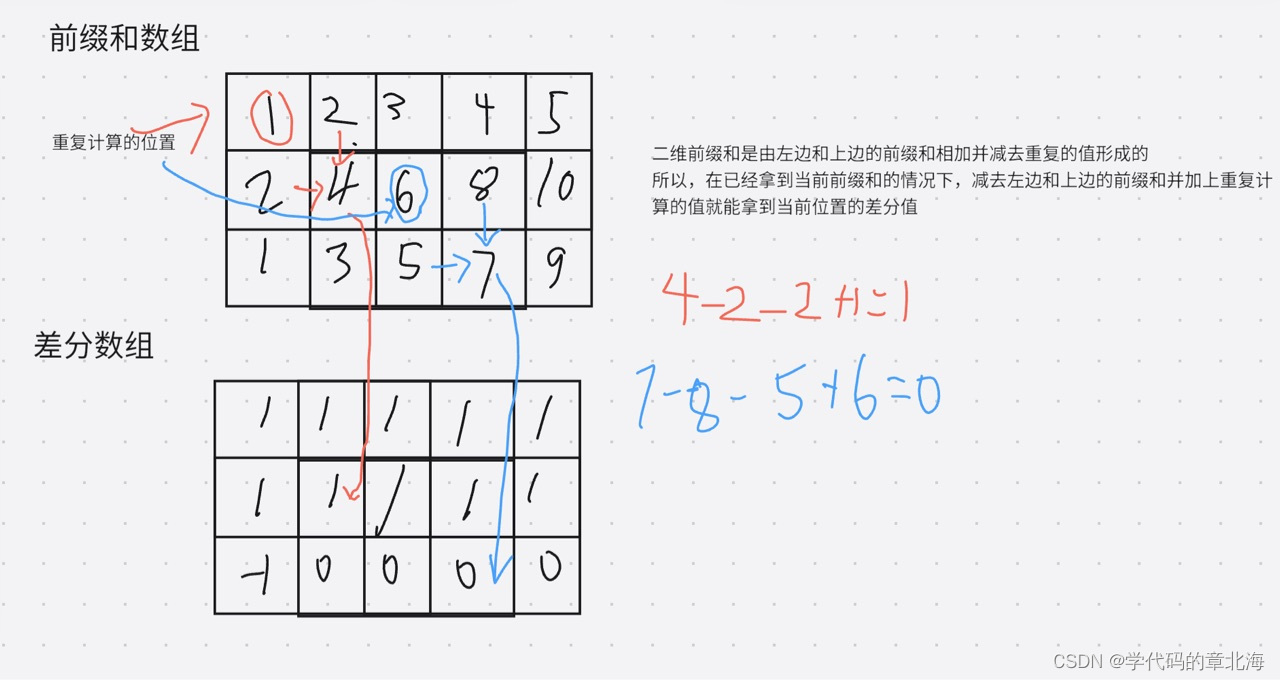
这样我们就拿到了差分数组接下来再根据要求对差分数组进行更改,比如说我们让中间一行除了最后一个值全部加上1.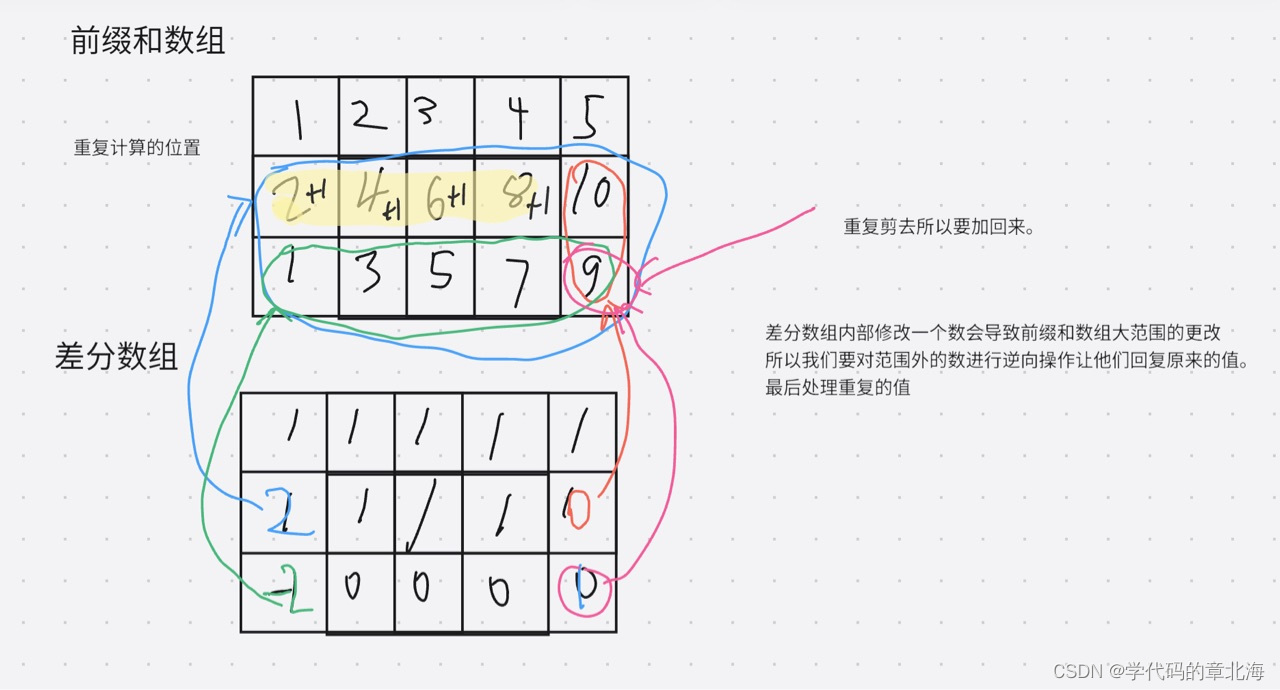
最后再求一遍二维前缀和就能拿到想要的值。
3.代码实现
const int N = 1010;
int dif[N][N];
int ori[N][N];
int main()
{
int n, m, q;
cin >> n >> m >> q;
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= m; j++)
{
cin >> ori[i][j];
dif[i][j] += ori[i][j]; //插入差分数组
dif[i][j + 1] -= ori[i][j];
dif[i + 1][j] -= ori[i][j];
dif[i + 1][j + 1] += ori[i][j];
}
}
//进行操作
while (q--)
{
int x1, x2, y1, y2, c;
cin >> x1 >> y1 >> x2 >> y2 >> c;
dif[x1][y1] += c; //修改差分数组
dif[x1][y2 + 1] -= c;
dif[x2 + 1][y1] -= c;
dif[x2 + 1][y2 + 1] += c;
}
//求回前缀和
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= m; j++)
{
dif[i][j] = dif[i][j] + dif[i-1][j]+dif[i][j-1]-dif[i-1][j-1];
}
}
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= m; j++)
{
cout << dif[i][j]<<" ";
}
puts("");
}
return 0;
}