详细分析置换算法

对于操作系统而言，虚拟空间是非常大的，我们往往无法直接将如此大的空间装入内存，而即使我们采用多级页表与段页式存储即使，也仅仅只是节省了页表的大小，如此将如何多的物理页装进内存仍然是一个问题，为此科学家们提出了一种动态的思想，当剩余空间不够装入新页面时，操作系统就选择适当的页将其刷新回磁盘(如果确实是脏页的话，如果不是脏页则仅仅只是覆盖)，以此空出空间装入新页，而这则需要运用到页面置换算法。

还有一个问题是：是否需要对每一个进程固定一个空间大小，换句话说，是采用局部分配策略还是全局分配策略。

采用局部分配的好处在于每一个进程空间都是互不影响的，即使一个进程频繁的发生页面置换也不会影响到其他进程，并且易于管理；但缺点是，如何分配一个进程的空间大小是难以确定的，有的进程可能频繁发生页面置换，而有的进程可能只会使用一点点空间，这是预先无法确定的，如果给一个进程分配的空间小了，那么该进程可能会发生内存“颠簸”(频繁的发生页面置换)。

若采用全局分配，一个进程理论上可以使用整个内存空间，内存大意味着发生置换的频率就小了，在绝大多数情况下，全局分配优于局部策略。但缺点也是很明显的，如果进程较多，一个进程频繁进行页面置换可能会置换其他进程的页，这可能会导致其他进程也造成缺页异常，需要引入新页，从而造成死循环。这是操作系统不愿意看到的事情，而且操作系统难以控制这种局面。

目前现代操作系统非常智能，现代操作系统大多采用局部分配的方法，这更易于操作系统控制。当操作系统开始分配页面时，会根据进程数量、进程资源大小等参数相对公平的分配固定的空间，例如总内存大小为 10kb，当已有一个资源为 5kb 的进程A正在运行，由于只有一个进程，进程A的空间大小为整个内存大小 10kb，现在操作系统打算为资源大小为 15kb 的进程B分配空间，操作系统根据进程大小与进程数量进行评估，由于进程B大小 : 进程A大小 = 3 : 1，因此操作系统为B分配 3/4 的内存空间大小 7.5kb，同时调整A的大小为 2.5kb(淘汰页面)。

在运行时，操作系统仍然会进行动态调整，如果一个进程A频繁的发生颠簸，而进程B几乎不发生颠簸，操作系统会适当增加进程A空间的大小，而减少进程B空间的大小。如果所有的进程都发生颠簸，这是最坏的情况，此时操作系统会选择一些进程将它们暂时的调换到磁盘中以空处一些空间，直到有新的空间时再将他们换回来。

何时会发生页面置换？程序执行期间，若程序所要访问的页面未在内存时，发生缺页异常(页表项中存在位为0)，需要引入该页。中断处理程序首先保留CPU环境，转入缺页中断处理程序。查找页表，得到该页在外存的物理块后，

如果内存未满，则将缺页调入内存并修改页表。

如果内存已满，则按照某种置换算法从内存中选出一页换出；如果该页未被修改过，可不必将该页写回磁盘；但如果此页已被修改，则必须将它写回磁盘，然后再把所缺的页调入内存，并修改页表中的相应表项，置其存在位为“1”，并将此页表项写入快表中。如果此时进程的内存空间不够，则需要淘汰一些页面，这就是页面置换。

在了解这些之后，让我们来具体探讨一些页面淘汰算法。

最佳置换(OPT)算法

选择的被淘汰页面，将是以后永不使用的，或许是在最长(未来)时间内不再被访问的页面；采用最佳置换算法可保证获得最低的缺页率。但是由于无法预知哪一个页面是未来最长时间内不再被访问的，因而该算法是无法实现的；

先进先出页面置换算法(First-In First-Out，FIFO)

FIFO 算法是一种比较容易实现的算法。它的思想是先进先出（FIFO，队列），这是最简单、最公平的一种思想，即如果一个数据是最先进入的，那么可以认为在将来它被访问的可能性很小。空间满的时候，最先进入的数据会被最早置换（淘汰）掉。

FIFO 算法的描述：设计一种缓存结构，该结构在构造时确定大小，假设大小为 K，并有两个功能：

set(key,value)：将记录(key,value)插入该结构。当缓存满时，将最先进入缓存的数据置换掉。
get(key)：返回key对应的value值。

实现：维护一个FIFO队列，按照时间顺序将各数据（已分配页面）链接起来组成队列，并将置换指针指向队列的队首。再进行置换时，只需把置换指针所指的数据（页面）顺次换出，并把新加入的数据插到队尾即可。

缺点：判断一个页面置换算法优劣的指标就是缺页率，而FIFO算法的一个显著的缺点是，在某些特定的时刻，缺页率反而会随着分配页面的增加而增加，这称为Belady现象。产生Belady现象现象的原因是，FIFO置换算法与进程访问内存的动态特征是不相容的，被置换的内存页面往往是被频繁访问的，或者没有给进程分配足够的页面，因此FIFO算法会使一些页面频繁地被替换和重新申请内存，从而导致缺页率增加。因此，现在不再使用FIFO算法。

我们可以简单的用一个数组来实现FIFO，每次淘汰第一个位置的数据，每次在尾部插入即可。

LRU算法

LRU（The Least Recently Used，最近最久未使用算法）是一种常见的缓存算法，在很多分布式缓存系统（如Redis, Memcached）中都有广泛使用。

LRU算法的思想是：如果一个数据在最近一段时间没有被访问到，那么可以认为在将来它被访问的可能性也很小。因此，当空间满时，最久没有访问的数据最先被置换（淘汰）。

LRU算法的描述：设计一种缓存结构，该结构在构造时确定大小，假设大小为 K，并有两个功能：

set(key,value)：将记录(key,value)插入该结构。当缓存满时，将最久未使用的数据置换掉。
get(key)：返回key对应的value值。

实现：最朴素的思想就是用数组+时间戳的方式，不过这样做效率较低。因此，我们可以用双向链表（LinkedList）+哈希表（HashMap）实现（链表用来表示位置，哈希表用来存储和查找），在Java里有对应的数据结构LinkedHashMap，数据结构为hashMap和双向链表。

核心思想为：通过在插入的节点间建立前后连接关系，并且增加指向头尾节点的指针，实现头结点删除，尾结点写入。访问过一次移动到尾结点，这样头结点为最久未使用数据。

LInkedHashMap

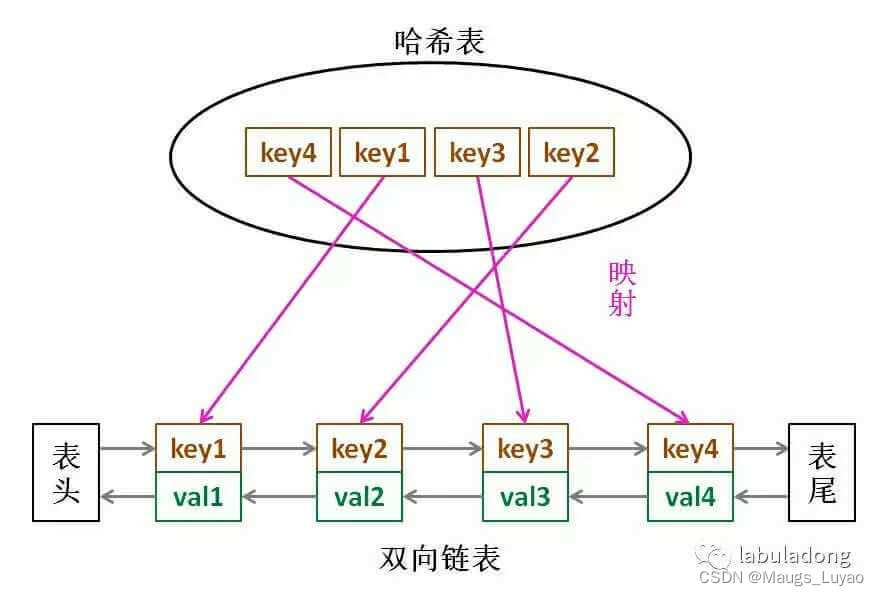
利用Java的LinkedHashMap用非常简单的代码来实现基于LRU算法的Cache功能

import java.util.LinkedHashMap;
import java.util.Map;
/**
 * 简单用LinkedHashMap来实现的LRU算法的缓存
 */
public class LRUCache<K, V> extends LinkedHashMap<K, V> {
    private int cacheSize;
    public LRUCache(int cacheSize) {
        super(16, (float) 0.75, true);
        this.cacheSize = cacheSize;
    }
    protected boolean removeEldestEntry(Map.Entry<K, V> eldest) {
        return size() > cacheSize;
    }
}

测试：

import org.slf4j.Logger;
import org.slf4j.LoggerFactory;

public class LRUCacheTest {
	private static final Logger log = LoggerFactory.getLogger(LRUCacheTest.class);
	private static LRUCache<String, Integer> cache = new LRUCache<>(10);

	public static void main(String[] args) {
		for (int i = 0; i < 10; i++) {
			cache.put("k" + i, i);
		}
		log.info("all cache :'{}'",cache);
		cache.get("k3");
		log.info("get k3 :'{}'", cache);
		cache.get("k4");
		log.info("get k4 :'{}'", cache);
		cache.get("k4");
		log.info("get k4 :'{}'", cache);
		cache.put("k" + 10, 10);
		log.info("After running the LRU algorithm cache :'{}'", cache);
	}
}

Output:

all cache :'{k0=0, k1=1, k2=2, k3=3, k4=4, k5=5, k6=6, k7=7, k8=8, k9=9}'
get k3 :'{k0=0, k1=1, k2=2, k4=4, k5=5, k6=6, k7=7, k8=8, k9=9, k3=3}'
get k4 :'{k0=0, k1=1, k2=2, k5=5, k6=6, k7=7, k8=8, k9=9, k3=3, k4=4}'
get k4 :'{k0=0, k1=1, k2=2, k5=5, k6=6, k7=7, k8=8, k9=9, k3=3, k4=4}'
After running the LRU algorithm cache :'{k1=1, k2=2, k5=5, k6=6, k7=7, k8=8, k9=9, k3=3, k4=4, k10=10}'

LFU算法

LFU（Least Frequently Used ，最近最少使用算法）也是一种常见的缓存算法。

顾名思义，LFU算法的思想是：如果一个数据在最近一段时间很少被访问到，那么可以认为在将来它被访问的可能性也很小。因此，当空间满时，最小频率访问的数据最先被淘汰。

LFU 算法的描述：

设计一种缓存结构，该结构在构造时确定大小，假设大小为 K，并有两个功能：

set(key,value)：将记录(key,value)插入该结构。当缓存满时，将访问频率最低的数据置换掉。
get(key)：返回key对应的value值。

LFU 算法相当于是把数据按照访问频次进行排序，这个需求恐怕没有那么简单，而且还有一种情况，如果多个数据拥有相同的访问频次，我们就得删除最早插入的那个数据。也就是说 LFU 算法是淘汰访问频次最低的数据，如果访问频次最低的数据有多条，需要淘汰最旧的数据。

算法实现策略：考虑到 LFU 会淘汰访问频率最小的数据，我们需要一种合适的方法按大小顺序维护数据访问的频率。LFU 算法本质上可以看做是一个 top K 问题(K = 1)，即选出频率最小的元素，因此我们很容易想到可以用二项堆来选择频率最小的元素，这样的实现比较高效。实现策略为小顶堆+哈希表或hash表。小顶堆这里可以根据频率进行排序后，选出最小的元素进行删除

这里先给出hash表结构

class LFUCache {
    // key 到 val 的映射
    HashMap<Integer, Integer> keyToVal;
    // key 到 freq 的映射
    HashMap<Integer, Integer> keyToFreq;
    // freq 到 key 列表的映射
    HashMap<Integer, LinkedHashSet<Integer>> freqToKeys;
    // 记录最小的频次
    int minFreq;
    // 记录 LFU 缓存的最大容量
    int cap;

    public LFUCache(int capacity) {
        keyToVal = new HashMap<>();
        keyToFreq = new HashMap<>();
        freqToKeys = new HashMap<>();
        this.cap = capacity;
        this.minFreq = 0;
    }

    public int get(int key) {}

    public void put(int key, int val) {}
}