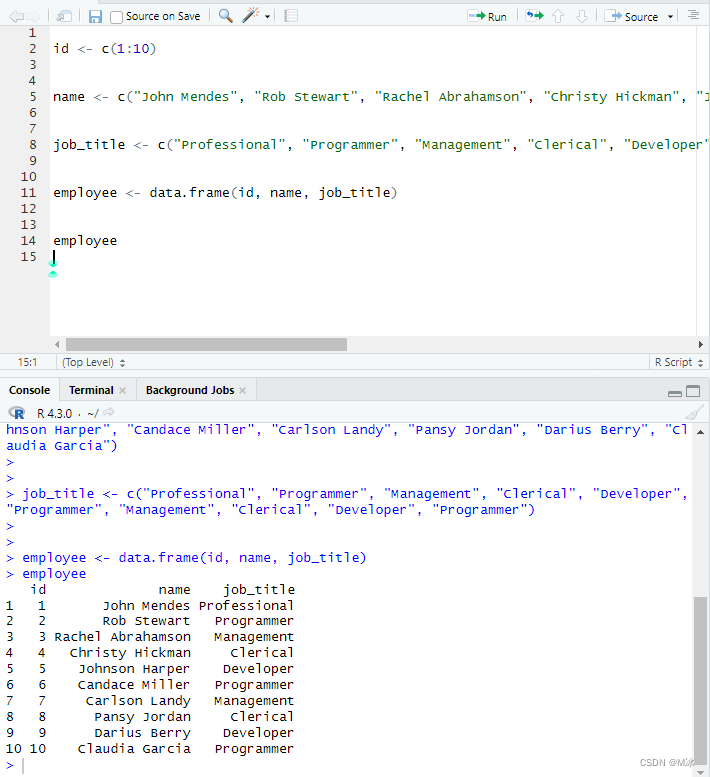
一、优先队列接口

• 记录一些项目，快速地访问/移除最重要的

  • 例：有限带宽的路由器，必须优先某些信息

  • 例：操作系统内核中的进程调度

  • 例：离散事件模拟（下一件事何时发生）

  • 例：图算法（接下来的课程中）

• 通过key有序的项目=优先，因此是集合接口（不是序列接口）

• 对集合特定操作子集进行了优化：

  • build(X)，由可迭代的X构建优先队列

  • insert(x)，添加项目x到数据结构

  • delete_max()，移除并返回拥有最大key的存储项目

  • find_max()，返回拥有最大key的存储项目

• 通常对最大或最小做出优化，而非全部

• 聚焦于insert和delete_max操作：build可以重复地insert；find_max可以是insert(delete_max())

二、优先队列排序

• 任何优先队列数据结构可以翻译为排序算法：

  • build(A)，按输入顺序，一个一个地插入项目

  • 重复地delete_min（或delete_max()）来决定（反向）顺序

• 所有艰难的工作发生在数据结构中

• 运行时间是：$T_{build}+n\ast T_{delete\_max}\le n\ast T_{insert}+n\ast T_{delete\_max}$

  我们已经看到的一些排序算法，可以被视作优先队列排序：

三、优先队列：集合AVL树

• 集合AVL树支持insert(x)，find_min()，find_max()，delete_min()，delete_max()花费$\mathcal{O}(\log n)$

• 因此优先队列排序花费$\mathcal{O}(n\log n)$

  • 这源自lecture 7的AVL排序

• 可以通过子树新增变量，加速find_min()和find_max()为耗时$\mathcal{O}(1)$

• 但这个数据结构是复杂的，结果排序是非in-place的

• 是否存在一个更简单的数据结构用于优先队列，并且是$\mathcal{O}(n\log n)$ 时间复杂度的in-place排序？存在，二项堆和堆排序

• 在序列数据结构（数组）之上，实现集合数据结构，使用我们学过的二叉树

四、优先队列：数组

• 存储项目到一个无序动态数组

• insert(x)：追加x到最后，花费摊还$\mathcal{O}(1)$

• delete_max()：花费$\mathcal{O}(n)$找到最大的，交换最大的到最后，然后删除

• insert是快的，但delete_max是慢的

• 优先队列排序是选择排序！（加上一些拷贝）

五、优先队列：有序数组

• 存储项目到有序动态数组

• insert(x)：在末尾追加x，花费$\mathcal{O}(n)$交换到有序的位置

• delete_max()：从末尾删除花费摊还$\mathcal{O}(1)$

• 优先队列排序是插入排序！（加上一些拷贝）

• 我们可以从两个极端的数组优先队列中找到折中？

六、数组作为一个完全的二叉树

• 想法：数组表示完全二叉树，除最大深度外，深度i处有$2^i$个点，所有点左对齐。

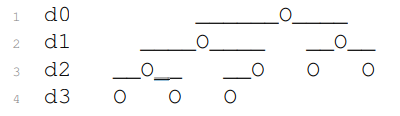
• 等价地，完全二叉数阅读顺序：从根到叶子、从左到右

• 数组和完全二叉树的双射

• 对应n个元素数组的完全二叉树高度为$\lceil \lg n\rceil$，因此是平衡二叉树

七、隐式完全二叉树

• 完全二叉树结构可以是隐式的，而非存储指针

• 根在索引0处

• 通过索引算式计算相邻点：left(i)=2i+1,right(i)=2i+2,parent(i)=$\lfloor \frac{i-1}{2}\rfloor$

八、二叉堆

• 想法：更大的元素在树中高度更高，仅局部如此

• 节点i处最大堆属性： Q [ i ] ≥ Q [ j ] , j ∈ { l e f t ( i ) , r i g h t ( i ) } Q[i]\ge Q[j],j\in\{left(i),right(i)\} Q[i]≥Q[j],j∈{left(i),right(i)}

• 最大堆是一个数组：所有节点满足最大堆属性

• 声明：在最大堆中，对于subtree(i)中所有节点j，每个节点i满足$Q[i]\ge Q[j]$

• 特别地，最大项目在最大堆的根部

九、堆插入

• 追加新项目x到数组末尾，耗费摊还$\mathcal{O}(1)$，生成它的下个叶子i（按读顺序）

• max_heapify_up(i)：与parent交换，直到满足最大堆属性

  • 检测$Q[parent(i)]\ge Q[i]$（parent(i)处最大堆属性的一部分）

  • 如果不是，交换Q[i]和Q[parent(i)]，递归max_heapify_up(parent(i))

• 正确性：

  • 最大堆属性保证所有节点>=子节点

  • 如果必须交换，Q[parent(i)]满足同样的保证，而非Q[i]

• 运行时间：树的高度，因此是$\Theta (\log n)$

十、堆删除最大

• 仅可以轻松地从动态数组中移除最后的项目，但最大的key是树的根

• 因此把根节点（i=0处的项目）与最后的项目（n-1处）交换

• max_heapify_down(i)：将根与更大的子节点交换，直到满足最大堆属性

  • 检查是否 Q [ i ] ≥ Q [ j ] , j ∈ { l e f t ( i ) , r i g h t ( i ) } Q[i]\ge Q[j],j \in \{left(i),right(i)\} Q[i]≥Q[j],j∈{left(i),right(i)}（位于i处的最大堆属性）

  • 如果不是，Q[i]和Q[j]进行交换（ j ∈ { l e f t ( i ) , r i g h t ( i ) } j\in\{left(i),right(i)\} j∈{left(i),right(i)}，有最大key的项目），并递归调用max_heapify_down(j)

• 正确性：

  • 最大堆属性保证所有节点>=子节点

  • 如果必须交换，Q[j]满足同样的保证，而非Q[i]

• 运行时间：树的高度，因此是$\Theta (\log n)$

十一、堆排序

• 添加最大堆到优先队列排序，给我们一个新的排序算法

• 运行时间是$\mathcal{O}(n\log n)$，因为每个insert和delete_max花费$\mathcal{O}(\log n)$

• 对于这个排序算法，通常包含两个提升

十二、in-place优先队列排序

• 最大堆Q是一个更大数组A的前缀，记录共有多少项目在堆中

• $|Q|$初始时为0，最终为$|A|$（插入完），然后再次为0（删除后）

• insert()吸收数组中下个项目（位于索引$|Q|$处）到堆

• delete_max()将最大的项目移到最后，然后通过降低$|Q|$来废弃它

• 数组in-place优先队列排序是选择排序

• 有序数组in-place优先队列排序是插入排序

• 二叉最大堆in-place优先队列排序是堆排序

十三、线性构建堆

• 插入n个项目到堆中，i从0到n-1调用max_heapify_up(i)（根下降）：

最坏情形交换：${\sum }_{i=0}^{n-1}depth(i)={\sum }_{i=0}^{n-1}\lg i=\lg (n!)\ge (n/2)\lg (n/2)=\Omega (n\lg n)$

• 将整个数组当作一个完全二叉树，i从n-1到0调用max_heapify_down(i)（叶子上升）：

最坏情形交换：${\sum }_{i=0}^{n-1}height(i)={\sum }_{i=0}^{n-1}(\lg n-\lg i)=\lg \frac{n^n}{n!}=\Theta (\lg \frac{n^n}{\sqrt{n}(n/e{)}^n})=\mathcal{O}(n)$

• 因此可以花费$\mathcal{O}(n)$构建堆

• 没有加速堆排序的性能（$\mathcal{O}(n\log n)$）

十四、序列AVL树优先队列

• 其他线性构建时间的对数数据结构，序列AVL树

• 以任意顺序（插入顺序）存储优先队列项目到序列AVL树

• 维持最大新增变量：node.max=指向node子树中拥有最大key的节点，这是一个子树属性，因此花费常量复杂度

• find_min()和find_max()花费$\mathcal{O}(1)$

• delete_min和delete_max花费$\mathcal{O}(\log n)$

• build(A)花费$\mathcal{O}(n)$

• 与二叉堆有相同的边界

十五、Set和Multiset

• 我们的集合接口假定没有重复key，我们可以使用这些集合实现Multiset，允许项目有重复key

  • 集合中的每个项目是一个序列（比如链表），存储了有同一个key的多个项目

• 实际上，除了这个方法，二叉堆和AVL树可以直接处理重复key的项目（比如delete_max删除有最大key的所有项目），注意使用<=，而不是集合AVL树中的<