树
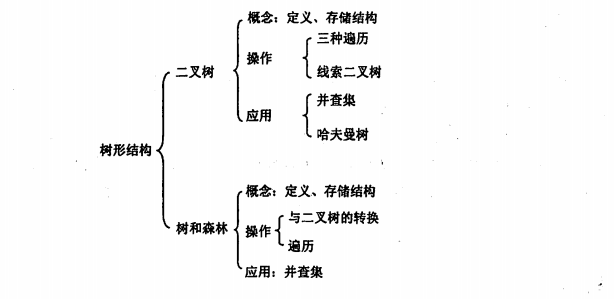
- 1 知识框架
- 2 二叉树概论
- 2.1 特殊二叉树
- 2.2 二叉树的存储
- 2.3 线索二叉树
1 知识框架
基本概念:
1.度:一个结点的孩子为该结点的度,树中最大度数为树的度。
2.深度,高度,层次:高度和层次都是从顶至下,高度是从底至上。
基本性质:
1.结点数 = 所有度数之和 + 1
2.具有n个结点的m叉数的最小高度
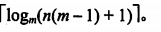
3.非空二叉树上的叶结点等于度为2的结点树+1
2 二叉树概论
2.1 特殊二叉树
1.满二叉树
高度为h,有2^h - 1个结点。
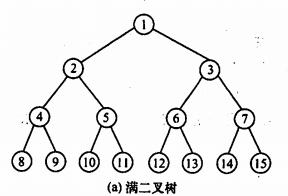
2.完全二叉树
叶结点的高度差不超过1且最下面结点从左往右,左边一个不缺。
3.二叉排序树
左 < 根 < 右 或者 右 < 根 < 左
树上的任何一颗子树都遵守
4.平衡二叉树
树上任何一个左右子树深度之差不超过1 (后面文章细讲平衡二叉树的插入与删除)
2.2 二叉树的存储
1.顺序存储
完全二叉树适合顺序存储,一般二叉树在存储时,空白结点也分配存储空间使他与完全二叉树一致
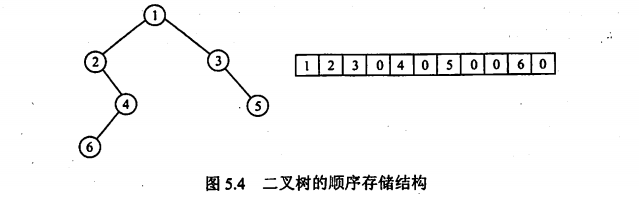
0表示不存在的空白结点
使用顺序存储时,数组下标从1开始,使他能符合完全二叉树的性质,如下:

2.链式存储
定义:
typedef struct tree{
ElemType data;
struct tree *lchild,*rchild;
int ltag,rtag;
}tree,*Tree;
树的建立和二叉树各种函数的应用(各种遍历,线索化)在前面的文章 二叉树函数总结
简单二叉树创立
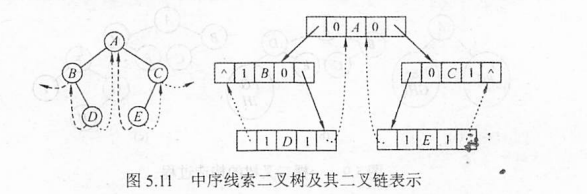
2.3 线索二叉树
定义:
若无左子树,lchild 指向前驱,ltag = 1;无右子树,rchild 指向后继,rtag = 1;
typedef struct ThreadTree
{
int data;
struct ThreadTree * lchid,rchild;
int ltag,rtag;
}ThreadTree,*ThreadTree
1.中序线索化
void midTreadTree(tree *p)//线索化方法
{
if(p != NULL){
midTreadTree(p -> lchild);//遍历左孩子
if(p -> lchild == NULL){
p -> ltag = 1;//为空,令标志=1;
p ->lchild = pre;//pre永远是指向上一个节点的指针
}
else {
p -> ltag = 0;//不为空令标志= 0;
}
if(pre -> rchild == NULL){
pre -> rtag = 1;
pre -> rchild = p;
}
else {
pre -> rtag = 0;
}
pre = p;
midTreadTree(p->rchild);//p指向当前节点,此时pre==p,p向后移动一位
}
}
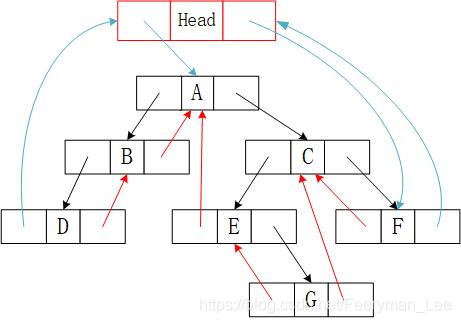
为了方便,还可以增加一个头结点:
2.先序线索化,后序线索化:递归的位置交换一下。