前言

树

树的概念

树的相关概念编辑

树的表示

二叉树的概念

特殊的二叉树

二叉树的存储结构

堆

堆的建立(本篇以小堆为例，大堆实现方法一样）

堆的结构定义

堆的初始化

堆的插入

堆的基础算法——向上调整算法

插入注意事项

堆的判空

堆的删除

堆的删除基础算法——向下调整算法

删除注意事项

堆的数据个数

取堆顶的数据

堆的销毁

堆排序

向上调整建堆

向下调整建堆

原理

Topk问题

原理（以求前k个最小的为例）

完整代码

前言

经过了栈和队列的学习，终于到达了树的环节啦！有的人可能疑惑标题不是堆吗？其实堆是由树组成的一种数据结构，在学习堆之前，我们会先简单地认识一下树

树

树的概念

树是一种非线性的数据结构，它是由n（n>=0）个有限结点组成一个具有层次关系的集合。把它叫做树是因为它看起来像一棵倒挂的树，也就是说它是根朝上，而叶朝下的。
有一个特殊的结点，称为根结点，根节点没有前驱结点。
除根节点外，其余结点被分成M(M>0)个互不相交的集合T1、T2、……、Tm，其中每一个集Ti(1<= i<= m)又是一棵结构与树类似的子树。每棵子树的根结点有且只有一个前驱，可以有0个或多个后继。
因此，树是递归定义的。

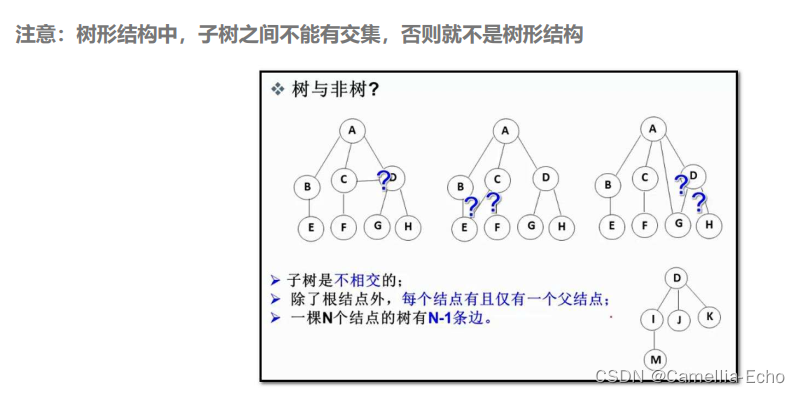
树的相关概念

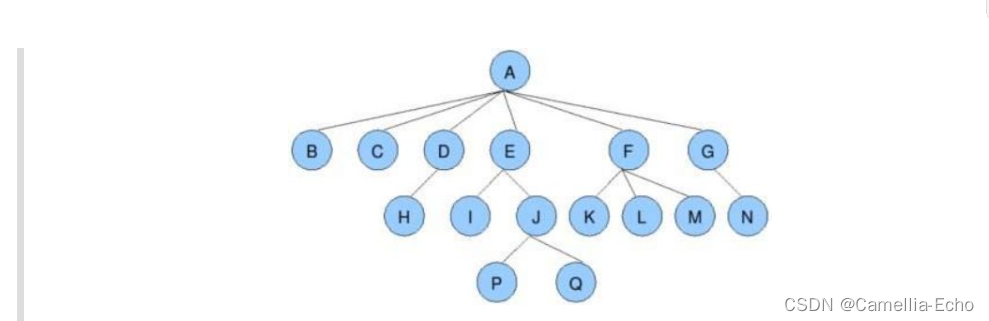
节点的度：一个节点含有的子树的个数称为该节点的度；如上图：A的为6
叶节点或终端节点：度为0的节点称为叶节点；如上图：B、C、H、I...等节点为叶节点
非终端节点或分支节点：度不为0的节点；如上图：D、E、F、G...等节点为分支节点
双亲节点或父节点：若一个节点含有子节点，则这个节点称为其子节点的父节点；如上图：A是B的父节点
孩子节点或子节点：一个节点含有的子树的根节点称为该节点的子节点；如上图：B是A的孩子节点
兄弟节点：具有相同父节点的节点互称为兄弟节点；如上图：B、C是兄弟节点
树的度：一棵树中，最大的节点的度称为树的度；如上图：树的度为6
节点的层次：从根开始定义起，根为第1层，根的子节点为第2层，以此类推；
树的高度或深度：树中节点的最大层次；如上图：树的高度为4
堂兄弟节点：双亲在同一层的节点互为堂兄弟；如上图：H、I互为兄弟节点
节点的祖先：从根到该节点所经分支上的所有节点；如上图：A是所有节点的祖先
子孙：以某节点为根的子树中任一节点都称为该节点的子孙。如上图：所有节点都是A的子孙
森林：由m（m>0）棵互不相交的树的集合称为森林

树的表示

树结构相对线性表就比较复杂了，要存储表示起来就比较麻烦了，既然保存值域，也要保存结点和结点之间的关系。

实际中树有很多种表示方式如：双亲表示法，孩子表示法、孩子双亲表示法以及孩子兄弟表示法等。我们这里就简单的了解其中最常用的孩子兄弟表示法。

typedef int DataType;
struct Node
{
struct Node* _firstChild1; // 第一个孩子结点
struct Node* _pNextBrother; // 指向其下一个兄弟结点
DataType _data; // 结点中的数据域
};

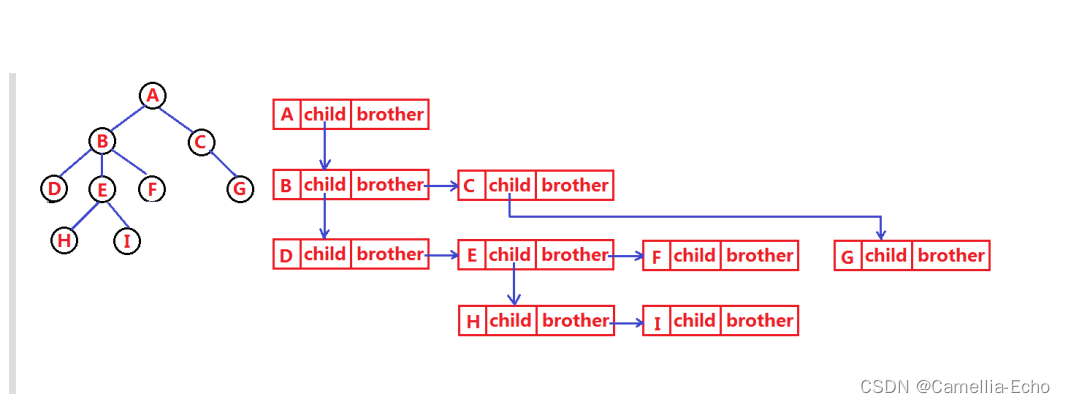
其实这种树在日常生活中非常常见，文件目录就是由孩子兄弟表示法的应用

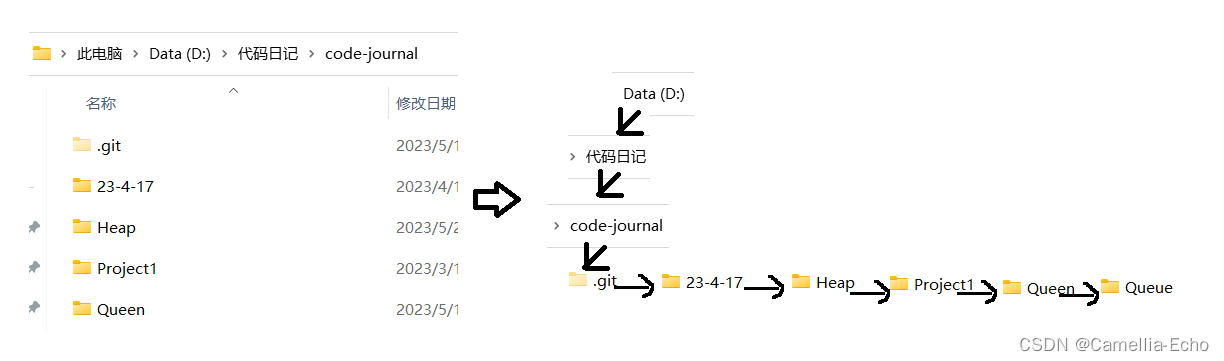
树可以是千奇百怪的，但是我们常用的是二叉树这种结构，那么什么是二叉树呢？

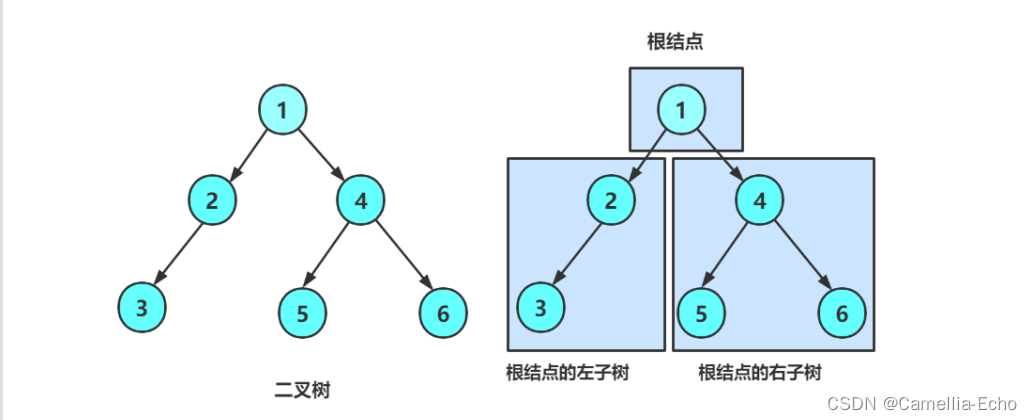
二叉树的概念

一棵二叉树是结点的一个有限集合，该集合:
1. 或者为空
2. 由一个根节点加上两棵别称为左子树和右子树的二叉树组成

从上图可以看出：

1. 二叉树不存在度大于2的结点
2. 二叉树的子树有左右之分，次序不能颠倒，因此二叉树是有序树

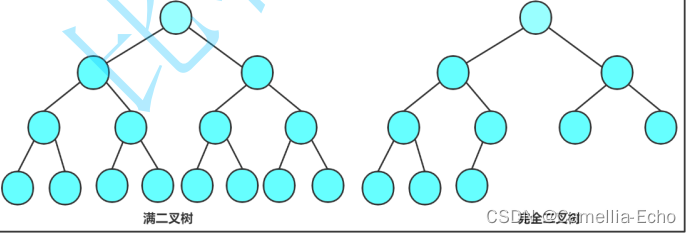
特殊的二叉树

1. 满二叉树：一个二叉树，如果每一个层的结点数都达到最大值，则这个二叉树就是满二叉树。也就是说，如果一个二叉树的层数为K，且结点总数是，则它就是满二叉树。
2. 完全二叉树：完全二叉树是效率很高的数据结构，完全二叉树是由满二叉树而引出来的。对于深度为K的，有n个结点的二叉树，当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树。要注意的是满二叉树是一种特殊的完全二叉树。也可以认为完全二叉树是按满二叉树截出来的·

二叉树的存储结构

如果是满二叉树或者是完全二叉树，那么就可以考虑使用数组存储，因为每个数据都是挨在一起的，就不存在过多的空间浪费

如果不是这两种特殊的二叉树，往往考虑链式存储以避免过多的空间浪费

如果用数组存储数据，那么父子之间的下标有如下关系

leftchild=parent*2+1；rightchild=parent*2+2
parent=（leftchild-1）/2或者（rightchild-1）/2

堆

经过了树的介绍，终于轮到我们的堆啦！

堆其实就是一种完全二叉树，用数组存储，不过多了一些限制条件：堆中某个节点的值总是不大于或不小于其父节点的值

总结以上就有堆的两点性质：

堆中某个节点的值总是不大于或不小于其父节点的值；
堆总是一棵完全二叉树。

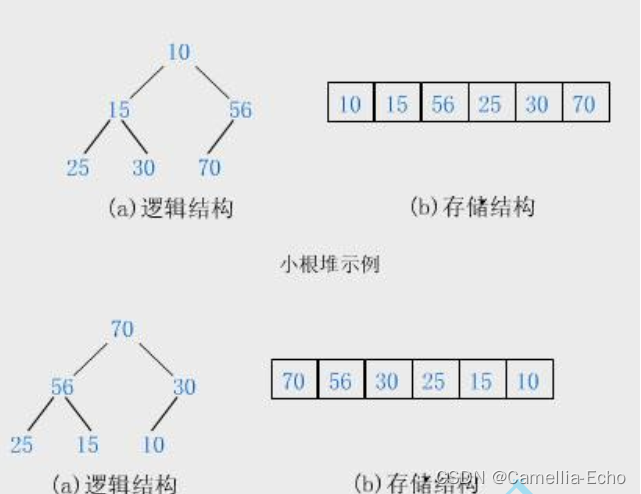
当某个节点的值总是不大于父节点的值的时候，堆顶的数据往往是最小的，所以其被称为小堆
当某个节点的值总是不小于父节点的值的时候，堆顶的数据往往是最大的，所以其被称为大堆

注意：堆只有父子之间有大小的比较关系，而兄弟之间并没有大小的关系，所以堆并不是有序的（关键，容易和二叉查找树混淆！！！）

堆的建立(本篇以小堆为例，大堆实现方法一样）

堆的结构定义

和栈同为数组，所以这里的结构定义的方式一模一样，不过后续的操作是完全不一样的，这里就不赘述了

typedef int HPDataType;
typedef struct Heap
{
	HPDataType* a;
	int size;
	int capacity;
}Heap;

堆的初始化

仍然是在插入的时候再开辟空间，此处置空指针即可
依然是老生常谈的问题——传进来的堆要存在，直接assert暴力断言即可，后续函数接口也仍然都要有这个操作，后续就不赘述了
指针置空，数据置0

void HeapInit(Heap*hp)
{
	assert(hp);
	hp->capacity = hp->size = 0;
	hp->a = NULL;
}

堆的插入

堆的基础算法——向上调整算法

堆的建立应该基于其性质之上——堆中某个节点的值总是不大于或不小于其父节点的值
因为不能保证插入数据后堆的性质不被破坏（因为对于插入的数据的前后大小关系未知），所以在每次插入数据后，都要进行一次调整
因为在堆中只有父子之间有关系，兄弟之间无关系，所以只用循环地对父子之间进行调整即可，我们称其为向上调整
一旦父子之间符合相关关系或者孩子到达堆顶的时候，跳出循环

代码如下：

//向上调整算法
void AdjustUp(Heap* hp, int child)
{
	int parent = (child - 1) / 2;
	while (child > 0)
	{
		if (hp->a[child] < hp->a[parent])
		{
			Swap(&hp->a[child], &hp->a[parent]);
			child = parent;
			parent = (child - 1) / 2;
		}
		else
		{
			break;
		}
	}
}

插入注意事项

在堆末尾插入数据后，对插入的数据进行向上调整操作，以保持堆的性质不变
进行向上调整之前size先++，size表示数据的个数，所以我们要对数组里下标为size-1的数据进行向上调整
如果size==capacity，就进行扩容操作

void HeapPush(Heap* hp, HPDataType x)
{
	assert(hp);
	//满了先扩容
	if (hp->capacity == hp->size)
	{
		int newcapacity = hp->capacity == 0 ? 4 : (hp->capacity * 2);
		HPDataType *tmp=(HPDataType*)realloc(hp->a,sizeof(HPDataType) * newcapacity);
		if (tmp == NULL)
		{
			perror("realloc fail\n");
			return;
		}
		hp->capacity = newcapacity;
		hp->a = tmp;
	}
	hp->a[hp->size] = x;
	hp->size++;

	AdjustUp(hp,hp->size-1);
}

堆的判空

和栈、顺序表一样，堆数据删除之前要有数据可删，所以要进行判空操作
将其封装成函数接口，可以提高代码的可读性

堆的删除

堆的删除基础算法——向下调整算法

堆的删除应该基于其性质之上——堆中某个节点的值总是不大于或不小于其父节点的值
这里的删除和顺序表以及栈一样，size--即可，并不是真的抹除数据
如果是和数组元素头删一样，那么就不能保证堆的性质不变
所以我们将堆末尾数据与堆顶数据交换，然后size--就将堆顶元素删除了，然后将堆顶元素依次和孩子比较并交换（小堆选择更小的那个孩子进行交换），我们称其为向下调整算法
一旦其符合相关父子关系或者没有孩子的时候就跳出循环

//向下调整算法
void AdjustDown(Heap* hp, int n, int parent)
{
	int child = parent * 2 + 1;

	while (child < n)
	{
		//从左右子树中找更小的一个孩子
		if (child+1<n && hp->a[child] > hp->a[child+1])
		{
			child++;
		}
		if (hp->a[parent] > hp->a[child])
		{
			Swap(&hp->a[parent], &hp->a[child]);
			parent = child;
			child = parent * 2 + 1;
		}
		else
		{
			break;
		}
	}
	
}

删除注意事项

删除之前先对堆进行判空，直接asser暴力断言即可
将堆顶元素与堆末尾数据交换后，先对size--，相当于将原来的堆顶数据抹除，再对堆顶数据进行向下调整，以保持堆的性质不变

代码如下：

// 堆的删除
void HeapPop(Heap*hp)
{
	assert(hp);
	assert(!HeapEmpty(&hp));

	Swap(&hp->a[0], &hp->a[hp->size - 1]);
	hp->size--;

	AdjustDown(hp, hp->size, 0);
}

堆的数据个数

size即表示堆的数据个数了，所以返回size即可

// 堆的数据个数
int HeapSize(Heap* hp)
{
	assert(hp);

	return hp->a[hp->size];
}

取堆顶的数据

判空，不为空直接返回即可

HPDataType HeapTop(Heap* hp)
{
	assert(hp);
	assert(!HeapEmpty(&hp));

	return hp->a[0];
}

堆的销毁

和栈的销毁一样，先free掉数组，然后指针置空
size，capacity置0

// 堆的销毁
void HeapDestory(Heap* hp)
{
	assert(hp);

	hp->a = NULL;
	hp->capacity = hp->size = 0;
}

堆这种数据结构其实并不适合用来存储数据，而是进行一些操作，比如实现堆排序和解topk问题，

这两个问题是堆的经典应用，在学习完堆的建立后就来看看吧

堆排序

堆排序可谓是堆的经典应用之一，也是一种很牛的排序算法，时间复杂度为 O（N*logN），这也是学习它的原因之一
对数组排序，也就是对数组建堆。升序建大堆，降序建小堆，等会以降序来解释这个结论，学会了降序，升序也就是换换大于号小于号的事情。
首先，我们要对数组建堆。这里可以用向上调整算法进行建堆，时间复杂度为O（N*logN），也可以用向下调整算法进行建堆，时间复杂度为O（N）
注意这里的建堆和上文的建堆过程并不一样，上文的建堆过程是向内存申请空间，开辟了一个堆，然后往里填数据，这里的过程只是模拟其过程，并不用新开辟空间，而是在原本的空间上进行操作

向上调整建堆

我们从第一个结点开始，依次对每个结点进行向上调整
i每加一次，就相当于与上文的数据的插入过程，然后对插入数据进行向上调整
这样等于每个结点都进行了一次向上调整，堆就建立好了

// 向上调整建堆
for (int i = 0; i <n; i++) 
{
    //AdjustUp里的大于号小于号决定了是大堆还是小堆
    AdjustUp(hp,hp->a[i]);
}

向下调整建堆

因为向上/向下建堆的前提都是要在堆上进行，而数组一开始又不是一个堆，那怎么用向下建堆的方法将数组建成堆呢？
一个结点，即可以是大堆，也可以是小堆。
我们从最后一个非终端结点依次往左进行向下调整，这样我们遍历了除了最后一层的所有结点，也完成了堆的建立

// 向下调整建堆
for (int i = (n -1-1) / 2; i >= 0; i--) 
{
    adjustdown(a, n, i);
}

当堆建立好后，堆排序就很轻松了，相当于模拟堆的删除过程。这里以降序为例（建小堆）

原理

小堆的堆顶是最小值，将其与堆末尾的数据交换后，这样最小的元素就到了数组的末尾了。然后我们对这个处在数组最后一个位置的最小元素视而不见，将交换过去的堆顶元素执行向下调整算法，这时，第二小的元素就到了堆顶，然后此时的堆顶元素继续与最后一个元素进行交换（注意第一个交换过去的最大的元素已经不在范围内了，也就是说每将一个当前最大的数交换过去后，可视作size减一一次），然后再将交换过去的堆顶元素执行向下调整算法…这样循环往复，最终该数组就变成了降序。

是不是非常amazing，这样就实现了一个N*logN的排序算法了

// 堆排序
void HeapSort(HPDataType* a, int n)
{
	assert(a);

	// 向下调整, 这里是建小堆
	for (int i = (n - 2) / 2; i >= 0; i--) adjustdown(a, n, i);

	//小堆即降序
	int k = n - 1;
	while (k > 0)
	{
		swap(&a[0], &a[k]);
		adjustdown(a, k, 0);
		k--;
	}
}

动图演示：网上找了一个升序的，看看过程即可，小堆也是类似的。因为动图制作时间成本有点大，暂时就不自己弄了

python-列表排序_QFIUNE的博客-CSDN博客_python列表排序

Topk问题

topk问题就是在成千上万的数据中找出排名靠前的前k个数据，什么热销榜好评榜都可以由堆来实现
因为只要求前k个，所以我们只要先将前k个数据建堆就好，不用将全部数据都建堆，不然会有很多的空间浪费
求前k个最小的建大堆，求前k个最大的建小堆

原理（以求前k个最小的为例）

先将前k个数据建堆，堆顶就是最大值，然后将其他数据与堆顶元素相比，如果比他小就将其与堆顶元素交换，然后就行向下调整。调整过后堆顶就是新的最大值了，然后再和下一个数据进行对比，如果比堆顶大，那就跳过该数据，让下一个数据进行与堆顶，如果小于堆顶，则将其与堆顶元素交换，然后就行向下调整.......r如此循环，就能求出前k个最小值了

总结：

求前k个最小值建大堆是为了依次把最大值都挑出去
求前k个最大值建小堆是为了依次把最小值挑出去

// topk问题
void PrintTopK(HPDataType* a, int n, int k)
{
	assert(a);
	
	// 开辟能够存放k个数据空间
	HPDataType* topk = (HPDataType*)malloc(sizeof(HPDataType) * k);
	if (topk == NULL)
	{
		perror("malloc fail");
		exit(-1);
	}
	// 前k个数据进堆
	memcpy(topk, a, sizeof(HPDataType) * k);

	// 找前k个最小的——建大堆
	for (int i = (k - 2) / 2; i >= 0; i--) adjustdown(topk, k, i);
	
	// 对topk堆进行除大进小的操作
	for (int i = k; i < n; i++)
	{
		if (a[i] < topk[0])
		{
			topk[0] = a[i];
			adjustdown(topk, k, 0);
		}
	}
}

因为堆是很重要的数据结构，也很难，反复琢磨怎么讲的更细。所以本篇写了比较久，希望大家多多支持啦！！！

感谢阅读本小白的博客，如有错误请指出，一定虚心采纳~

完整代码

#include"Heap.h"

// 堆的构建
void HeapInit(Heap*hp)
{
	assert(hp);
	hp->capacity = hp->size = 0;
	hp->a = NULL;
}
// 堆的插入
void HeapPush(Heap* hp, HPDataType x)
{
	assert(hp);
	//满了先扩容
	if (hp->capacity == hp->size)
	{
		int newcapacity = hp->capacity == 0 ? 4 : (hp->capacity * 2);
		HPDataType *tmp=(HPDataType*)realloc(hp->a,sizeof(HPDataType) * newcapacity);
		if (tmp == NULL)
		{
			perror("realloc fail\n");
			return;
		}
		hp->capacity = newcapacity;
		hp->a = tmp;
	}
	hp->a[hp->size] = x;
	hp->size++;

	AdjustUp(hp,hp->size-1);
}
// 堆的删除
void HeapPop(Heap*hp)
{
	assert(hp);
	assert(!HeapEmpty(&hp));

	Swap(&hp->a[0], &hp->a[hp->size - 1]);
	hp->size--;

	AdjustDown(hp, hp->size, 0);
}
// 取堆顶的数据
HPDataType HeapTop(Heap* hp)
{
	assert(hp);
	assert(!HeapEmpty(&hp));

	return hp->a[0];
}
// 堆的数据个数
int HeapSize(Heap* hp)
{
	assert(hp);

	return hp->a[hp->size];
}
// 堆的判空
bool HeapEmpty(Heap* hp)
{
	assert(hp);
	
	return hp->size == 0;
}
// 堆的销毁
void HeapDestory(Heap* hp)
{
	assert(hp);

	hp->a = NULL;
	hp->capacity = hp->size = 0;
}
//向上调整算法
void AdjustUp(Heap* hp, int child)
{
	int parent = (child - 1) / 2;
	while (child > 0)
	{
		if (hp->a[child] < hp->a[parent])
		{
			Swap(&hp->a[child], &hp->a[parent]);
			child = parent;
			parent = (child - 1) / 2;
		}
		else
		{
			break;
		}
	}
}
//向下调整算法
void AdjustDown(Heap* hp, int n, int parent)
{
	int child = parent * 2 + 1;

	while (child < n)
	{
		//从左右子树中找更小的一个孩子
		if (child+1<n && hp->a[child] > hp->a[child+1])
		{
			child++;
		}
		if (hp->a[parent] > hp->a[child])
		{
			Swap(&hp->a[parent], &hp->a[child]);
			parent = child;
			child = parent * 2 + 1;
		}
		else
		{
			break;
		}
	}
	
}

void Swap(HPDataType* p1, HPDataType* p2)
{
	HPDataType tmp = *p1;
	*p1 = *p2;
	*p2 = tmp;
}