一. 什么是布隆过滤器

在我之前的博客C++：使用位图处理海量数据_【Shine】光芒的博客-CSDN博客中，介绍了如何使用位图来处理海量数据，位图的特点为：

速度快，节省空间。
采用直接定值法，不存在哈希冲突。
只适用于整形数据。

为了解决位图只适用于整形数据的问题，布隆过滤器被提了出来，是哈希表和位图结合的一种数据结构，主要用于处理海量字符串数据。

布隆过滤器的设计思想为：给定一个关键值Key，通过哈希函数，将其转换为size_t类型的数据，记为hashi，这里的hashi对应一个比特位，如果Key存在，它对应的二进制位就是1。我们可以认为，布隆过滤器的底层也是通过位图来实现的，是对位图的封装。

布隆过滤器和位图的不同在于：位图直接使用整形数据映射比特位，属于直接定值法，而布隆过滤器要对整形数据进行进一步转换（一般使用除留余数法）后映射到对应二进制位。

但是，如果只给定一个哈希函数，就很容易存在哈希冲突，从而导致误判：

如果判定为存在，那么有可能是误判，因为即使给定的key值不在，它也可能与某个存在的关键值冲突。
如果判定为不存在，则不可能是误判。

布隆过滤器的误判不可能完全避免，但是可以采取一定的优化措施，来降低误判率。

让一个值映射多个比特位可以降低误判概率，从理论上讲，一个值映射的比特位越多，误判概率越低，但是消耗的空间也越大。

布隆过滤器具有很强的实际应用价值，其在实际应用中分为允许误判和不允许误判两种情况：

不允许误判：如黑名单通缉系统，所有的黑名单人员信息都被存储在远端数据库，而前端存储了数据库的布隆过滤器信息。当前端接收到一个人的信息要判断它是否在黑名单时，先走前端的布隆过滤器，如果布隆过滤器返回的结果为不在，那么不可能误判，直接返回。如果布隆过滤器的结果为在，那么就需要通过网络连接远端数据库，在数据库中匹配信息，判断是否是误判。
允许误判：注册账号时，判断用户自定义的用户名是否和已有用户名冲突，如果冲突要求用户重新定义用户名。这里允许误判，所有直接走近端的布隆过滤器即可，无需再通过远端的数据库确认是否误判。

二. 布隆过滤器的实现

假设布隆过滤器共设置了3个哈希函数，分别记为Hash1、Hash2、Hash3，即：1个key值对应3个比特位。布隆过滤器类有一个成员变量_bst，自定义类型位图，N为待插入数据的个数。

代码2.1：布隆过滤器声明

//布隆过滤器（一般用于字符串）
//Hash1/2/3的默认值为三个字符串哈希函数，这是为了降低误判概率
template<size_t N, class K = std::string, class Hash1 = BKDRHash, class Hash2 = APHash, class Hash3 = DJBHash>
class BloomFilter
{
public:
	void set(const K& key);   //数据插入函数
	bool test(const K& key);  //数据查找函数

private:
	static const size_t ratio = 5;   //比例因子
	zhang::bitset<N * ratio> _bst;   //位图
};

2.1 数据插入函数set

获取到要插入的key数据（一般为string）后，通过三个哈希函数将key转换为3个不同的整形数据，将三个整形位置对应的比特位都置为1即可。

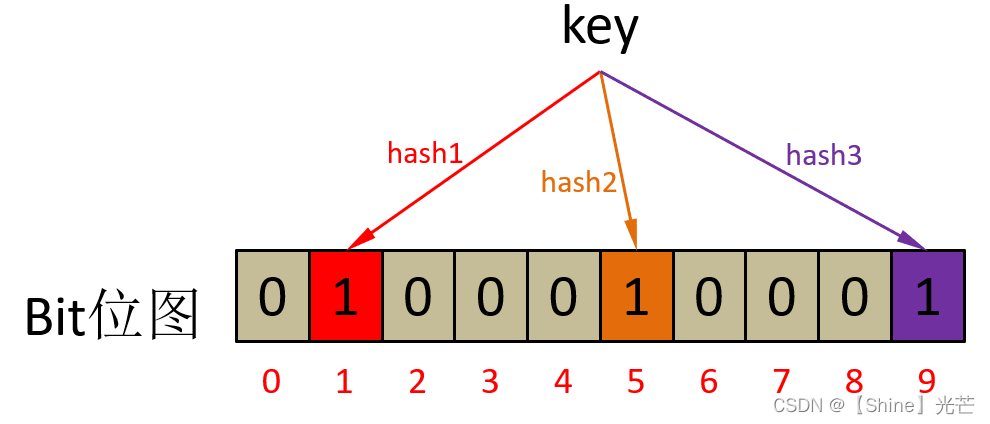
代码2.2：set函数

	//一个关键值key对应三个不同的哈希函数，有三个不同的位置
	//set函数将三个对应的bit位全部置1
	void set(const K& key)
	{
		size_t hash1 = Hash1()(key) % (N * ratio);
		size_t hash2 = Hash2()(key) % (N * ratio);
		size_t hash3 = Hash3()(key) % (N * ratio);

		_bst.set(hash1);
		_bst.set(hash2);
		_bst.set(hash3);
	}

2.2 判断数据是否存在函数test

检查key值对应的n个bit位是否全部为1，如果有一个是0，则表明key不存在。注意，如果判定为存在，那么可能是由于哈希冲突造成的，可能是误判。

代码2.3：test函数

	bool test(const K& key)
	{
		size_t hash1 = Hash1()(key) % (N * ratio);
		if (!_bst.test(hash1))
			return false;

		size_t hash2 = Hash2()(key) % (N * ratio);
		if (!_bst.test(hash2))
			return false;

		size_t hash3 = Hash3()(key) % (N * ratio);
		if (!_bst.test(hash3))
			return false;

		//三个哈希函数映射的二进制位都是1，表示存在
		return true;
	}

2.3 布隆过滤器数据的删除

一般而言，布隆过滤器是不支持数据删除的，但是，也并非不可以实现。如果采用一般形式的一个key对应多个比特位的布隆过滤器，那么直接在删除key时将它对应的比特位置0，那会影响到其它的值，让其它存在的值被误判为不存在，这是布隆过滤器所不允许的。

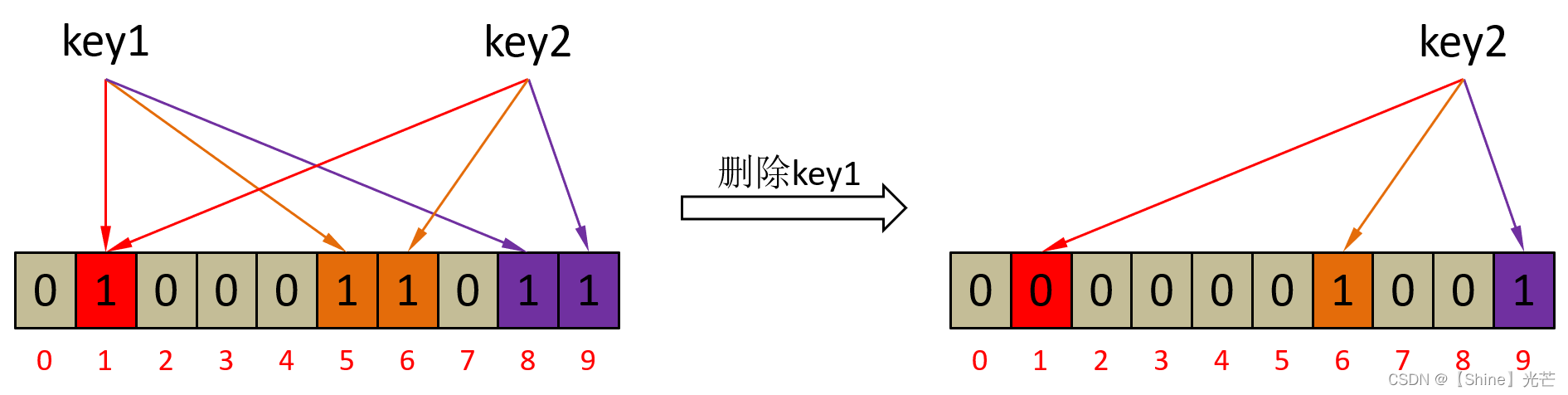
我们可以通过将每个bit位扩展为一个小计数器，来解决数据删除问题。这样原本一个Hash(key)计算值由映射到一张位图中的一个bit位，变为映射到多种位图中的多个bit位。假设布隆过滤器中有两张位图，两个位图特定位置中的两个bit为表示这个位置被映射到的次数。11表示3次，10表示2次，01表示一次。删除数据时，计数器的值-1即可。

但是，布隆过滤器如果支持删除，必然会引起空间消耗量的上升，却依旧无法完全避免误删除问题，布隆过滤器最大的优势之一就是空间消耗少，如果支持删除这一优势就会大打折扣，因此一般不需要布隆过滤器支持数据删除。

三. 哈希切分

本文从两个海量数据处理问题入手，讲述哈希切分。

问题1：给定两个含有100亿个query(字符串)的文件，如何精确查找两个文件的交集？

我们假设一个query占用20bytes的空间，那么100亿个query就占用2000亿bytes的空间，也就是200G，显然，内存无法容纳这么多数据。

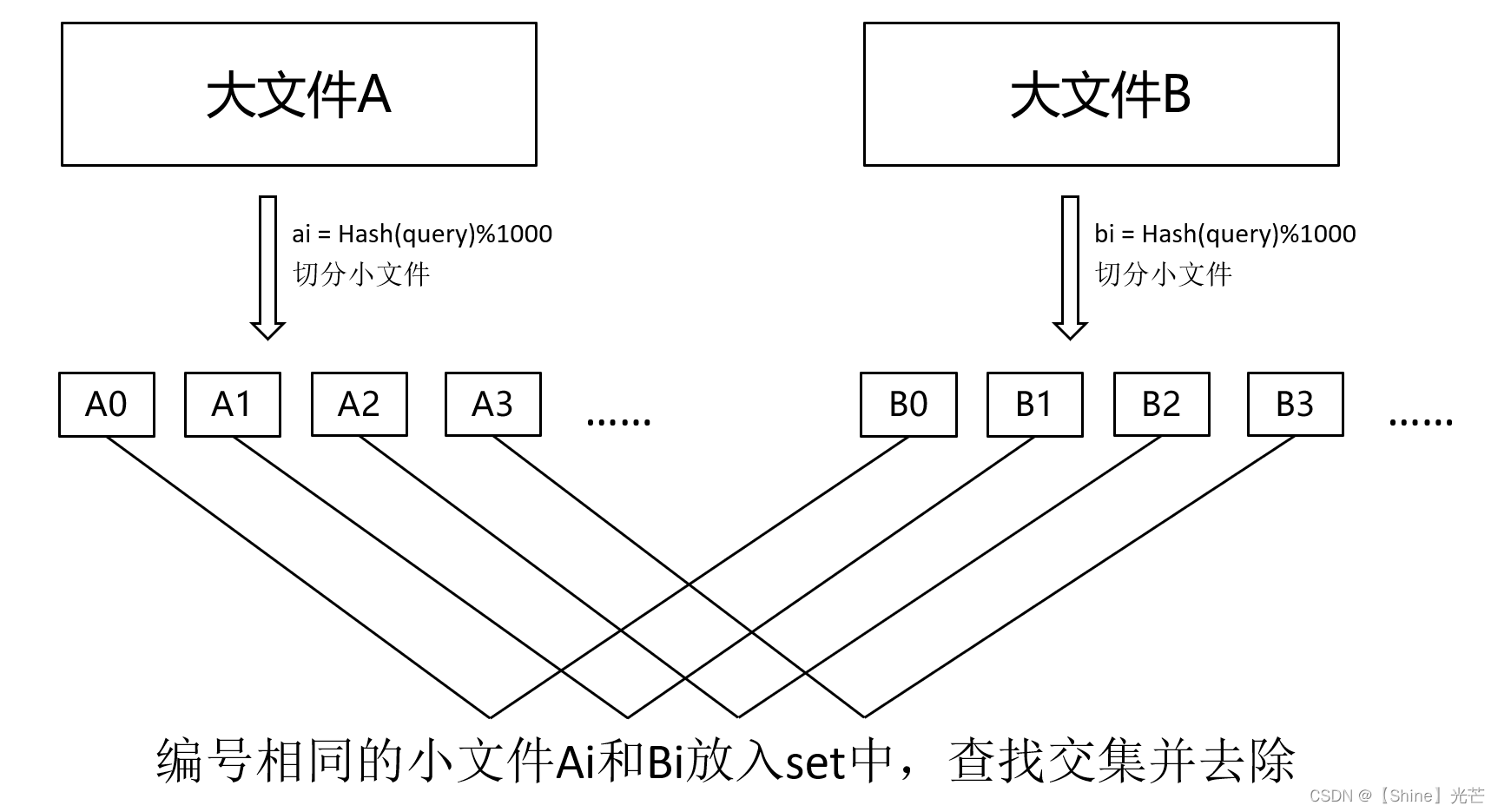
处理大文件的一种常用方法是将大文件均分为N个小文件，我们假设将问题中的一个文件均分为1000个小文件，将一个大文件切分出来的每个小文件，与另一个文件中的每个小文件进行比较，查找交集，这样确实可以找出两个大文件的交集，但效率十分低下。

为了高效查找大文件交集，我们采用哈希切分的方法。假设两个大文件分别叫做A和B，并将每个大文件切分为1000个小文件，从0~999对每个小文件进行编号，读取A和B文件中的每个query，根据i=Hash(query)%1000，将query放入对应编号的小文件中。这样可以保证相同的query被放入相同编号的小文件中，最终只需要比较大文件A和B编号相同的小文件找交集即可。

查找交集的方法：将两个小文件中的query放入到两个set中去，从begin()位置开始遍历两个set，如遇到相同值，就是小文件交集。这样还可以实现去重功能。

问题2：给定一个超过100G的日志文件，里面存储了若干IP地址，如何找出出现次数最多的K个IP地址（topK问题）

这里也要采用哈希切割的思想解决问题。将Log大文件切分为N个小文件，编号从0~N，根据i=Hash(IP)%N，计算每个IP应该放入到哪个小文件中，这样可以保证相同的IP在相同的小文件中。完成切分后，使用map<string, int>对每个小文件中的每个IP出现的次数进行统计，然后使用小堆结构，统计出现次数最多的K个IP。