张量场
张量场表示张量 T ( x ⃗ , t ) T(\vec x, t) T(x,t)在空间 x ⃗ \vec x x和时间 t t t中如何变化,将张量场视为可微函数
如果一个张量场不依赖于时间,则此张量场称为定常场,例如 T = T ( x ⃗ ) T = T(\vec x) T=T(x);相反,如果一个张量场只依赖时间则称为均匀场,就是说 T ( t ) T(t) T(t)在每个位置 x ⃗ \vec x x都有相同的值
张量场可以分类为:标量、向量、二阶张量场等
例如温度场
T
(
x
⃗
,
t
)
T(\vec x, t)
T(x,t) 就是一个标量场,在时间
t
=
t
1
t = t_1
t=t1中温度的分布如下:
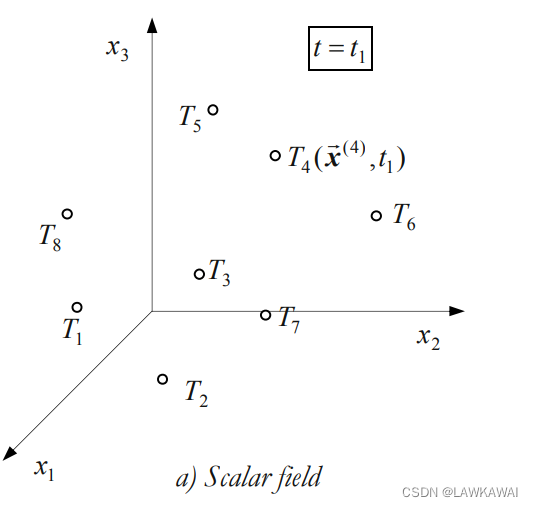
另外,速度场
v
⃗
(
x
⃗
,
t
)
\vec v(\vec x, t)
v(x,t)是一个向量场,在时间
t
=
t
1
t = t_1
t=t1的速度分布,在每一个点都有一个速度相对应,如下所示:

标量场:
ϕ
=
ϕ
(
x
⃗
,
t
)
\phi=\phi(\vec x, t)
ϕ=ϕ(x,t)
向量场:
张量表示:
v
⃗
=
v
⃗
(
x
⃗
,
t
)
\vec v = \vec v (\vec x, t)
v=v(x,t)
下标表示:
v
i
=
v
i
(
x
⃗
,
t
)
v_i = v_i(\vec x, t)
vi=vi(x,t)
二阶张量场:
张量表示:
T
=
T
(
x
⃗
,
t
)
T=T (\vec x, t)
T=T(x,t)
下标表示:
T
i
j
=
T
i
j
(
x
⃗
,
t
)
T_{ij}= T_{ij}(\vec x, t)
Tij=Tij(x,t)
标量场
定常标量场
ϕ
=
ϕ
(
x
⃗
)
\phi = \phi(\vec x)
ϕ=ϕ(x),有连续的值
∂
ϕ
∂
x
1
,
∂
ϕ
∂
x
2
,
∂
ϕ
∂
x
3
\frac{\partial \phi}{\partial x_1}, \frac{\partial \phi}{\partial x_2}, \frac{\partial \phi}{\partial x_3}
∂x1∂ϕ,∂x2∂ϕ,∂x3∂ϕ。在点
x
⃗
\vec x
x的函数值为
ϕ
(
x
⃗
)
\phi(\vec x)
ϕ(x),在另一个点
x
⃗
+
d
x
⃗
\vec x + d\vec x
x+dx的函数值为
ϕ
(
x
⃗
+
d
x
⃗
)
\phi(\vec x + d\vec x)
ϕ(x+dx),那么函数
ϕ
\phi
ϕ的微分定义如下:
ϕ
(
x
⃗
+
d
x
⃗
)
−
ϕ
(
x
⃗
)
≡
d
ϕ
ϕ
(
x
1
+
d
x
1
,
x
2
+
d
x
2
,
x
3
+
d
x
3
)
−
ϕ
(
x
1
,
x
2
,
x
3
)
≡
d
ϕ
\phi(\vec x + d\vec x)-\phi(\vec x)\equiv d\phi\\ \phi(x_1+dx_1, x_2+dx_2, x_3+dx_3)-\phi(x_1, x_2, x_3)\equiv d\phi
ϕ(x+dx)−ϕ(x)≡dϕϕ(x1+dx1,x2+dx2,x3+dx3)−ϕ(x1,x2,x3)≡dϕ
对于任意的连续函数
ϕ
(
x
1
,
x
2
,
x
3
)
\phi(x_1, x_2, x_3)
ϕ(x1,x2,x3),
d
ϕ
d\phi
dϕ 与
d
x
1
,
d
x
2
,
d
x
3
dx_1, dx_2, dx_3
dx1,dx2,dx3线性相关,这种线性关系可以以微分的链式法则来给出:
d
ϕ
=
∂
ϕ
∂
x
1
d
x
1
+
∂
ϕ
∂
x
2
d
x
2
+
∂
ϕ
∂
x
3
d
x
3
d\phi = \frac{\partial \phi}{\partial x_1}dx_1+\frac{\partial \phi}{\partial x_2}dx_2+\frac{\partial \phi}{\partial x_3}dx_3
dϕ=∂x1∂ϕdx1+∂x2∂ϕdx2+∂x3∂ϕdx3
张量的分量关于
x
i
x_i
xi的导数,可以由以下微分算子表示:
∂
∗
∂
x
i
≡
∗
,
i
\frac{\partial \ast}{\partial x_i}\equiv \ast_{,i}
∂xi∂∗≡∗,i
梯度
标量场的梯度:
梯度
∇
x
⃗
ϕ
\nabla_{\vec x}\phi
∇xϕ 或者
g
r
a
d
ϕ
grad \phi
gradϕ定义为:
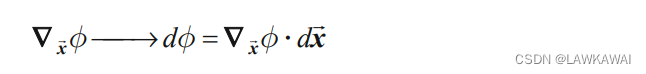
其中,算子
∇
x
⃗
\nabla_{\vec x}
∇x叫Nabla符号,将上式表示成笛卡尔坐标基:
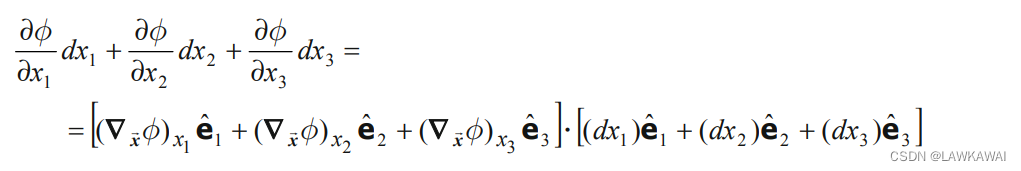
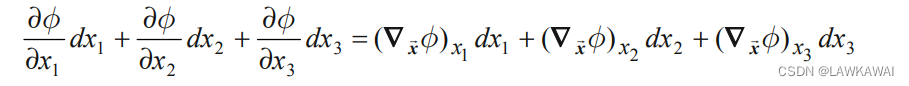
所以,
∇
x
⃗
ϕ
\nabla_{\vec x}\phi
∇xϕ在笛卡尔坐标系中的分量:
(
∇
x
⃗
)
1
≡
∂
ϕ
∂
x
1
;
(
∇
x
⃗
)
2
≡
∂
ϕ
∂
x
2
;
(
∇
x
⃗
)
3
≡
∂
ϕ
∂
x
3
;
(\nabla_{\vec x})_1 \equiv \frac{\partial \phi}{\partial x_1}; \quad (\nabla_{\vec x})_2 \equiv \frac{\partial \phi}{\partial x_2}; \quad (\nabla_{\vec x})_3 \equiv \frac{\partial \phi}{\partial x_3}; \quad
(∇x)1≡∂x1∂ϕ;(∇x)2≡∂x2∂ϕ;(∇x)3≡∂x3∂ϕ;
那么,梯度的分量定义如下:
∇
x
⃗
ϕ
=
∂
ϕ
∂
x
1
e
^
1
+
∂
ϕ
∂
x
2
e
^
2
+
∂
ϕ
∂
x
3
e
^
3
\nabla_{\vec x}\phi=\frac{\partial \phi}{\partial x_1}\hat e_1+\frac{\partial \phi}{\partial x_2}\hat e_2+\frac{\partial \phi}{\partial x_3}\hat e_3
∇xϕ=∂x1∂ϕe^1+∂x2∂ϕe^2+∂x3∂ϕe^3
Nabla符号
∇
x
⃗
\nabla_{\vec x}
∇x定义为:
∇
x
⃗
=
∂
∂
x
i
e
^
i
≡
∂
,
i
e
^
i
\boxed{\nabla_{\vec x}=\frac{\partial }{\partial x_i}\hat e_i\equiv \partial_{,i}\hat e_i}
∇x=∂xi∂e^i≡∂,ie^i
∇ , x ⃗ \nabla_{,\vec x} ∇,x的几何意义:
- ∇ x ⃗ \nabla_{\vec x} ∇x的方向是垂直于等值面的,例如垂直于等值面 ϕ = c o n s t \phi = const ϕ=const。 ∇ x ⃗ \nabla_{\vec x} ∇x的方向指向 ϕ \phi ϕ增长最快的方向
- ∇ x ⃗ \nabla_{\vec x} ∇x的大小是 ϕ \phi ϕ改变的速率,例如 ϕ \phi ϕ的梯度
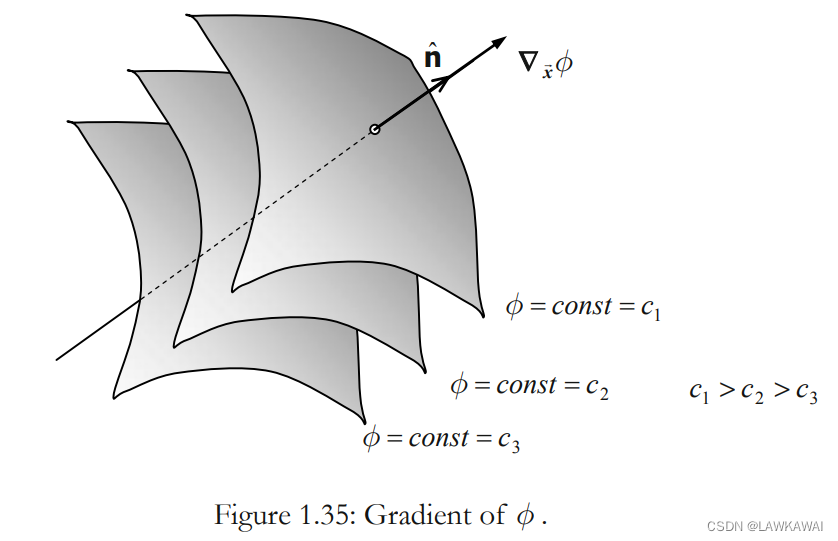
一个曲面的法向量如下所示:
n
^
=
∇
x
⃗
ϕ
∣
∣
∇
x
⃗
ϕ
∣
∣
\hat n = \frac{\nabla_{\vec x}\phi}{||\nabla_{\vec x}\phi||}
n^=∣∣∇xϕ∣∣∇xϕ
曲面
ϕ
=
c
o
n
s
t
\phi = const
ϕ=const,为等值面,在所有的点上都有相同的值,所以在等值面上移动函数值不发生改变
向量场
v
⃗
(
x
⃗
)
\vec v (\vec x)
v(x)的梯度:
g
r
a
d
(
v
⃗
)
≡
∇
x
⃗
v
⃗
grad(\vec v)\equiv\nabla_{\vec x}\vec v
grad(v)≡∇xv
表示成:
∇
x
⃗
v
⃗
=
∂
v
i
e
^
i
∂
x
j
⨂
e
^
j
=
(
v
i
e
^
i
)
,
j
⨂
e
^
j
=
v
i
,
j
e
^
i
⨂
e
^
j
\nabla_{\vec x}\vec v=\frac{\partial v_i \hat e_i}{\partial x_j}\bigotimes \hat e_j=(v_i \hat e_i)_{,j}\bigotimes \hat e_j=v_{i,j}\hat e_i \bigotimes \hat e_j
∇xv=∂xj∂vie^i⨂e^j=(vie^i),j⨂e^j=vi,je^i⨂e^j
因此,可以在笛卡尔坐标系中定义一个张量场
(
∗
(
x
⃗
,
t
)
)
(*(\vec x, t))
(∗(x,t))的梯度为:
∇
x
⃗
(
∗
)
=
∂
∗
∂
x
j
⨂
e
^
j
(
在笛卡尔坐标系中的张量场的梯度
)
\boxed{\nabla_{\vec x}(*)=\frac{\partial *}{\partial x_j}\bigotimes \hat e_j}(在笛卡尔坐标系中的张量场的梯度)
∇x(∗)=∂xj∂∗⨂e^j(在笛卡尔坐标系中的张量场的梯度)
二阶张量场的梯度:
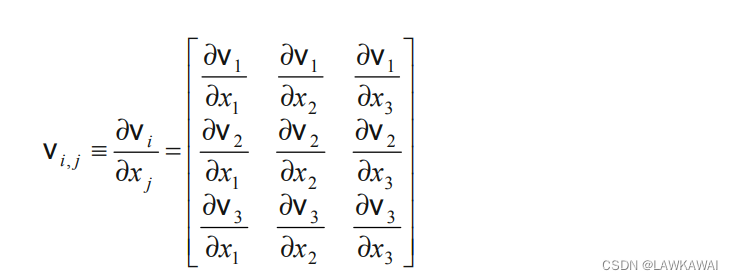
二阶张量场
T
(
x
⃗
)
T(\vec x)
T(x)的梯度:
∇
x
⃗
T
=
∂
T
i
j
e
^
i
⨂
e
^
j
∂
x
k
⨂
e
^
k
=
T
i
j
,
k
e
^
i
⨂
e
^
j
⨂
e
^
k
\nabla_{\vec x}T = \frac{\partial T_{ij}\hat e_i \bigotimes \hat e_j}{\partial x_k}\bigotimes \hat e_k=T_{ij, k}\hat e_i\bigotimes \hat e_j \bigotimes \hat e_k
∇xT=∂xk∂Tije^i⨂e^j⨂e^k=Tij,ke^i⨂e^j⨂e^k
表示为:
(
∇
x
⃗
T
)
i
j
k
=
T
i
j
,
k
(\nabla_{\vec x}T)_{ijk}=T_{ij,k}
(∇xT)ijk=Tij,k
问题1.41求出函数 f ( x 1 , x 2 ) = cos ( x 1 ) + exp x 1 x 2 f(x_1, x_2)=\cos(x_1)+\exp^{x_1x_2} f(x1,x2)=cos(x1)+expx1x2在点 ( x 1 = 0 , x 2 = 1 ) (x_1=0, x_2=1) (x1=0,x2=1) 的梯度

问题1.42 u ⃗ ( x ⃗ ) \vec u(\vec x) u(x)是一个定常场


散度
向量场
v
⃗
(
x
⃗
)
\vec v(\vec x)
v(x)的散度,标记如下:
d
i
v
(
v
⃗
)
≡
∇
x
⃗
⋅
v
⃗
div(\vec v)\equiv \nabla_{\vec x}\cdot \vec v
div(v)≡∇x⋅v
表示为:
d
i
v
(
v
⃗
)
≡
∇
x
⃗
⋅
v
⃗
=
∇
x
⃗
v
⃗
:
1
=
T
r
(
∇
x
⃗
v
⃗
)
div(\vec v)\equiv\nabla_{\vec x}\cdot \vec v=\nabla_{\vec x}\vec v:1=Tr(\nabla_{\vec x}\vec v)
div(v)≡∇x⋅v=∇xv:1=Tr(∇xv)
那么:
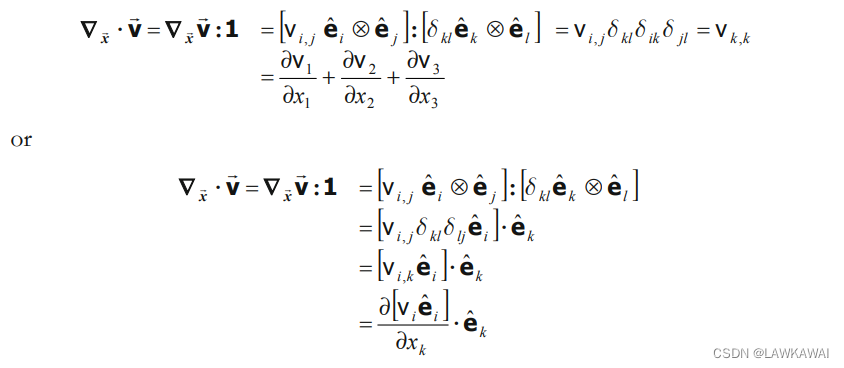
笛卡尔坐标系下的算子:
∇
x
⃗
⋅
(
∗
)
=
∂
(
∗
)
∂
x
k
⋅
e
^
k
(
笛卡尔坐标系下
(
∗
)
的散度
)
\boxed{\nabla_{\vec x}\cdot (*)=\frac{\partial (*)}{\partial x_k}\cdot \hat e_k}(笛卡尔坐标系下(*)的散度)
∇x⋅(∗)=∂xk∂(∗)⋅e^k(笛卡尔坐标系下(∗)的散度)
可以验证,当张量场作用散度时,其秩降低一阶
二阶张量场 T ( x ⃗ ) T(\vec x) T(x)的散度:
二阶张量场
T
T
T的散度定义为
∇
x
⃗
⋅
1
=
∇
x
⃗
T
:
1
\nabla_{\vec x}\cdot 1=\nabla_{\vec x}T:1
∇x⋅1=∇xT:1,得到一个向量:
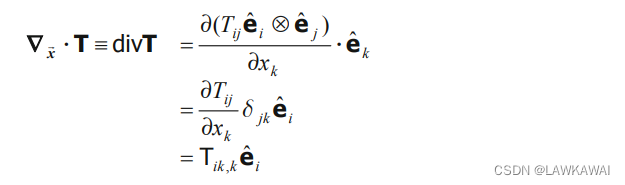
NOTE:注意了,在处理张量场的梯度和散度时,
例如
∇
x
⃗
v
⃗
\nabla_{\vec x}\vec v
∇xv(向量场的梯度)、
∇
x
⃗
T
\nabla_{\vec x}T
∇xT(二阶张量场的梯度)、
∇
x
⃗
⋅
T
\nabla_{\vec x}\cdot T
∇x⋅T(二阶张量场的散度),这不意味着在对向量和张量之间进行张量算子操作,
例如
∇
x
⃗
v
⃗
≠
(
∇
⃗
x
⃗
)
⨂
v
⃗
\nabla_{\vec x}\vec v\neq ( \vec \nabla_{\vec x})\bigotimes \vec v
∇xv=(∇x)⨂v,
∇
x
⃗
T
≠
(
∇
⃗
x
⃗
)
⨂
v
⃗
\nabla_{\vec x}T\neq (\vec \nabla_{\vec x})\bigotimes \vec v
∇xT=(∇x)⨂v以及
∇
x
⃗
⋅
T
≠
(
∇
⃗
x
⃗
)
⋅
(
T
)
\nabla_{\vec x}\cdot T \neq (\vec \nabla_{\vec x})\cdot (T)
∇x⋅T=(∇x)⋅(T),等
∇ x ⃗ \nabla_{\vec x} ∇x必须是一个作用在完整张量场的算子,所以张量必须在算子的内部
然而,可以有如下表示:

定义 拉普拉斯算子
∇
2
\nabla^2
∇2 为:
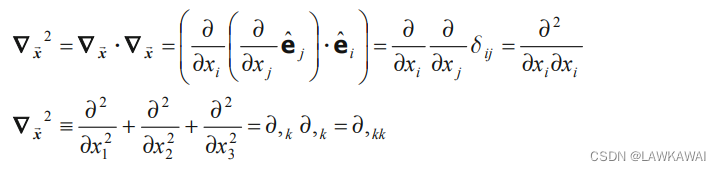
那么,向量场
v
⃗
\vec v
v的拉普拉斯向量为:
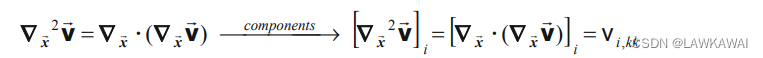
问题1.43 令 a ⃗ \vec a a和 b ⃗ \vec b b是向量,证明等式 ∇ x ⃗ ⋅ ( a ⃗ + b ⃗ ) = ∇ x ⃗ ⋅ a ⃗ + ∇ x ⃗ ⋅ b ⃗ \nabla_{\vec x}\cdot (\vec a + \vec b)=\nabla_{\vec x}\cdot \vec a+\nabla_{\vec x}\cdot \vec b ∇x⋅(a+b)=∇x⋅a+∇x⋅b成立

问题1.44 求出 ( ∇ x ⃗ a ⃗ ) ⋅ b ⃗ (\nabla_{\vec x}\vec a)\cdot \vec b (∇xa)⋅b
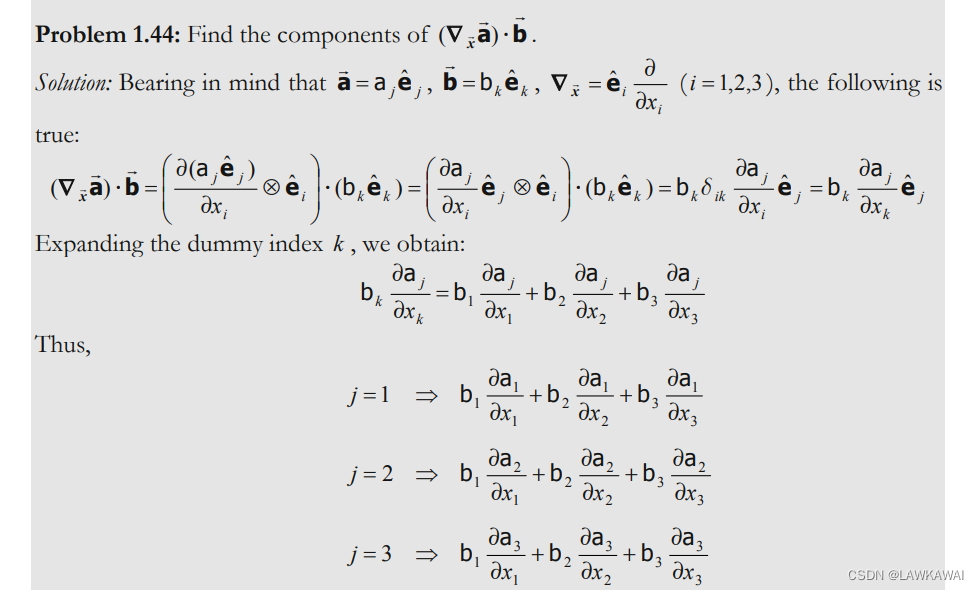
问题1.45 证明以下关系成立
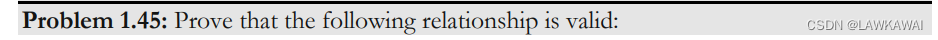

旋度
向量场的旋度:
向量场
v
⃗
(
x
⃗
)
\vec v(\vec x)
v(x)的旋度:
c
u
r
l
(
v
⃗
)
≡
r
o
t
(
v
⃗
)
≡
∇
x
⃗
∧
v
⃗
curl(\vec v)\equiv rot(\vec v)\equiv \nabla_{\vec x} \wedge \vec v
curl(v)≡rot(v)≡∇x∧v,并且用笛卡尔坐标基表示:
∇
⃗
x
⃗
∧
(
∗
)
=
∂
∂
x
j
e
^
j
∧
(
∗
)
(
在笛卡尔坐标系下的张量场的旋度
)
\boxed{\vec \nabla_{\vec x}\wedge (*)=\frac{\partial }{\partial x_j}\hat e_j \wedge (*)(在笛卡尔坐标系下的张量场的旋度)}
∇x∧(∗)=∂xj∂e^j∧(∗)(在笛卡尔坐标系下的张量场的旋度)
指标形式:
r
o
t
(
v
⃗
)
=
∇
⃗
x
⃗
∧
v
⃗
=
∂
∂
x
j
e
^
j
∧
v
⃗
k
e
^
k
=
∂
v
k
∂
x
j
e
^
j
∧
e
^
k
=
∂
v
k
∂
x
j
ϵ
i
j
k
e
^
i
=
ϵ
i
j
k
v
k
,
j
e
^
i
rot(\vec v)=\vec \nabla_{\vec x}\wedge \vec v=\frac{\partial }{\partial x_j}\hat e_j\wedge \vec v_k \hat e_k=\frac{\partial v_k}{\partial x_j}\hat e_j\wedge \hat e_k =\frac{\partial v_k}{\partial x_j}\epsilon_{ijk}\hat e_i=\epsilon_{ijk}v_{k,j}\hat e_i
rot(v)=∇x∧v=∂xj∂e^j∧vke^k=∂xj∂vke^j∧e^k=∂xj∂vkϵijke^i=ϵijkvk,je^i
展开:
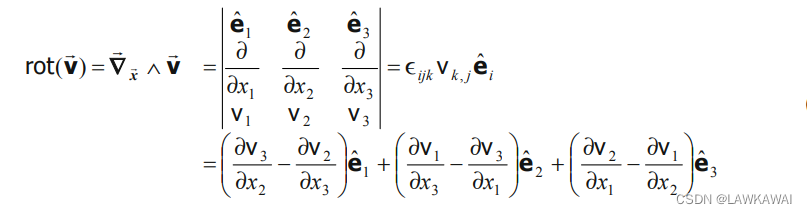
可以验证,一个向量场梯度的反对称部分,即
(
∇
x
⃗
v
⃗
)
s
k
e
w
≡
W
(\nabla_{\vec x}\vec v)^{skew}\equiv W
(∇xv)skew≡W,有如下分量:
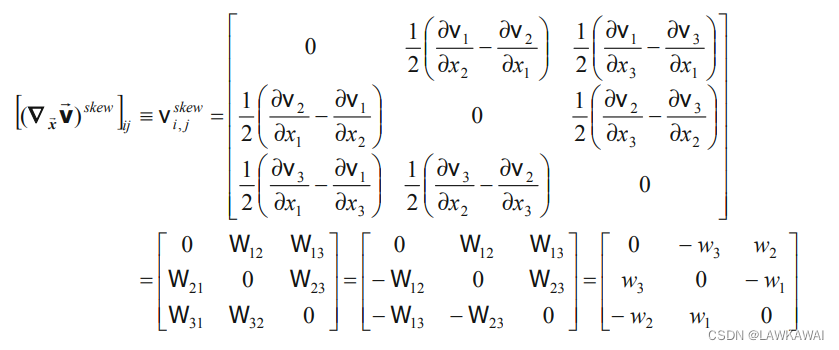
其中,
w
1
,
w
2
,
w
3
w_1, w_2, w_3
w1,w2,w3是W的轴向量
w
⃗
\vec w
w的分量
所以,结合旋度的定义和反对称矩阵分量,得到:
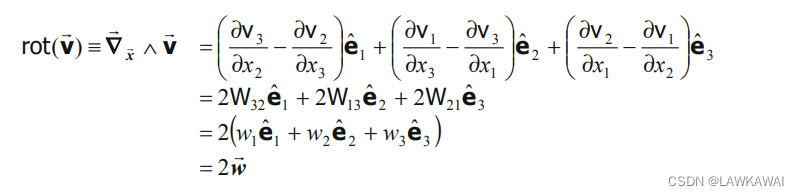
由于反对称张量和轴向量有以下关系:
W
⋅
a
⃗
=
w
⃗
∧
a
⃗
\boxed{W \cdot \vec a=\vec w \wedge \vec a}
W⋅a=w∧a
所以:
W
⋅
v
⃗
=
w
⃗
∧
v
⃗
=
1
2
(
∇
⃗
x
⃗
∧
v
⃗
)
∧
v
⃗
W \cdot \vec v=\vec w \wedge \vec v=\frac{1}{2}(\vec \nabla_{\vec x} \wedge \vec v)\wedge \vec v
W⋅v=w∧v=21(∇x∧v)∧v
我们在问题1.18里证明了反对称张量 ( x ⃗ ⨂ a ⃗ ) s k e w (\vec x \bigotimes \vec a)^{skew} (x⨂a)skew的轴向量是 1 2 ( a ⃗ ∧ x ⃗ ) \frac{1}{2}(\vec a \wedge \vec x) 21(a∧x),因此反对称张量 W = ( ∇ ⃗ x ⃗ v ⃗ ) s k e w = [ ( v ⃗ ) ⨂ ∇ ⃗ x ⃗ ] s k e w W = (\vec \nabla_{\vec x}\vec v)^{skew}=[(\vec v) \bigotimes \vec \nabla_{\vec x}]^{skew} W=(∇xv)skew=[(v)⨂∇x]skew的轴向量是 1 2 ( ∇ ⃗ x ⃗ ∧ v ⃗ ) \frac{1}{2}(\vec \nabla_{\vec x}\wedge \vec v) 21(∇x∧v)
如上所示,旋度描述了向量场的旋转趋势
总结:
-
r o t ( λ a ⃗ ) = ∇ ⃗ x ⃗ ∧ ( λ a ⃗ ) = λ ( ∇ ⃗ x ⃗ ∧ a ⃗ ) + ( ∇ x ⃗ λ ∧ a ⃗ ) rot(\lambda \vec a)=\vec \nabla_{\vec x}\wedge (\lambda \vec a)=\lambda (\vec \nabla_{\vec x}\wedge \vec a)+( \nabla_{\vec x} \lambda \wedge \vec a) rot(λa)=∇x∧(λa)=λ(∇x∧a)+(∇xλ∧a)
∇ ⃗ x ⃗ ∧ ( λ a ⃗ ) \vec \nabla_{\vec x}\wedge (\lambda \vec a) ∇x∧(λa)的结果是一个向量,分量为:
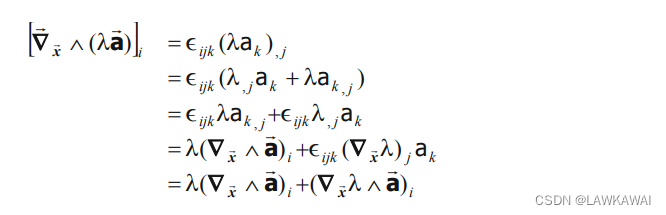
所以有: r o t ( λ a ⃗ ) = ∇ ⃗ x ⃗ ∧ ( λ a ⃗ ) = λ ( ∇ ⃗ x ⃗ ∧ a ⃗ ) + ( ∇ x ⃗ λ ∧ a ⃗ ) rot(\lambda \vec a)=\vec \nabla_{\vec x}\wedge (\lambda \vec a)=\lambda(\vec \nabla_{\vec x}\wedge \vec a)+(\nabla_{\vec x}\lambda \wedge \vec a) rot(λa)=∇x∧(λa)=λ(∇x∧a)+(∇xλ∧a) -
∇ ⃗ x ⃗ ∧ ( a ⃗ ∧ b ⃗ ) = ( ∇ x ⃗ ⋅ b ⃗ ) a ⃗ − ( ∇ a ⃗ ⋅ a ⃗ ) b ⃗ + ( ∇ x ⃗ a ⃗ ) ⋅ b ⃗ − ( ∇ x ⃗ b ⃗ ) ⋅ a ⃗ \vec \nabla_{\vec x}\wedge (\vec a \wedge \vec b)=(\nabla_{\vec x}\cdot \vec b)\vec a-(\nabla_{\vec a}\cdot \vec a)\vec b+(\nabla_{\vec x}\vec a)\cdot \vec b-(\nabla_{\vec x}\vec b)\cdot \vec a ∇x∧(a∧b)=(∇x⋅b)a−(∇a⋅a)b+(∇xa)⋅b−(∇xb)⋅a
由于有: ( a ⃗ ∧ b ⃗ ) = ϵ k i j a i b j (\vec a \wedge \vec b)=\epsilon_{kij}a_ib_j (a∧b)=ϵkijaibj,因此:
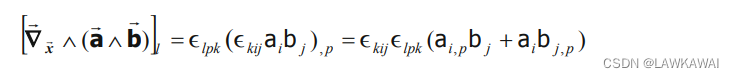
并且有: ϵ k i j = ϵ i j k \epsilon_{kij}=\epsilon_{ijk} ϵkij=ϵijk且 ϵ i j k ϵ l p k = δ i l δ j p − δ i p δ j l \epsilon_{ijk}\epsilon_{lpk}=\delta_{il}\delta_{jp}-\delta_{ip\delta_{jl}} ϵijkϵlpk=δilδjp−δipδjl,那么:
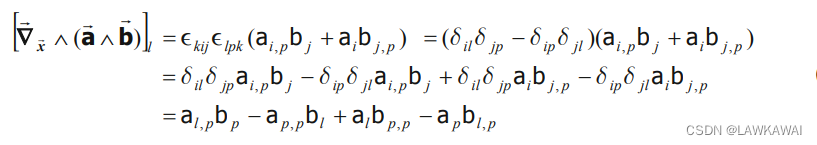
可以验证: [ ( ∇ x ⃗ a ⃗ ) ⋅ b ⃗ ] l = a l , p b p [(\nabla_{\vec x}\vec a)\cdot \vec b]_l=a_{l,p}b_p [(∇xa)⋅b]l=al,pbp, [ ( ∇ x ⃗ ⋅ a ⃗ ) b ⃗ ] l = a p , p b l [(\nabla_{\vec x}\cdot \vec a)\vec b]_l=a_{p,p}b_l [(∇x⋅a)b]l=ap,pbl, [ ( ∇ x ⃗ ⋅ b ⃗ ) a ⃗ ] l = a l b p , p [(\nabla_{\vec x}\cdot \vec b)\vec a]_l=a_lb_{p,p} [(∇x⋅b)a]l=albp,p, [ ( ∇ x ⃗ b ⃗ ) ⋅ a ⃗ ] l = a p b l , p [(\nabla_{\vec x} \vec b)\cdot \vec a]_l=a_pb_{l,p} [(∇xb)⋅a]l=apbl,p -
∇ ⃗ x ⃗ ∧ ( ∇ ⃗ x ⃗ ∧ a ⃗ ) = ∇ x ⃗ ( ∇ x ⃗ ⋅ a ⃗ ) − ∇ x ⃗ 2 a ⃗ \vec \nabla_{\vec x}\wedge (\vec \nabla_{\vec x}\wedge \vec a)=\nabla_{\vec x}(\nabla_{\vec x}\cdot \vec a)-\nabla_{\vec x}^2 \vec a ∇x∧(∇x∧a)=∇x(∇x⋅a)−∇x2a
由于: ( ∇ x ⃗ ∧ a ⃗ ) i = ϵ i j k a k , j (\nabla_{\vec x}\wedge \vec a)_i=\epsilon_{ijk}a_k,j (∇x∧a)i=ϵijkak,j,因此:
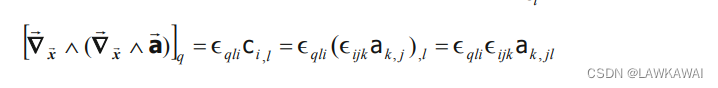
考虑: ϵ q l i ϵ i j k = ϵ q l i ϵ j k i = δ q j δ l k − δ q k δ l j \epsilon_{qli}\epsilon_{ijk}=\epsilon_{qli}\epsilon_{jki}=\delta_{qj}\delta_{lk}-\delta_{qk}\delta_{lj} ϵqliϵijk=ϵqliϵjki=δqjδlk−δqkδlj,有:
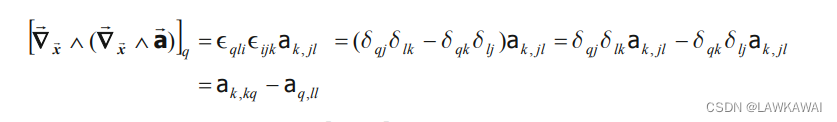
其中, [ ∇ x ⃗ ( ∇ x ⃗ ⋅ a ⃗ ) ] q = a k , k q [\nabla_{\vec x}(\nabla_{\vec x}\cdot \vec a)]_q=a_{k,kq} [∇x(∇x⋅a)]q=ak,kq和 [ ∇ x ⃗ 2 a ⃗ ] q = a q , l l [\nabla_{\vec x}^2\vec a]_q=a_{q,ll} [∇x2a]q=aq,ll -
∇ x ⃗ ⋅ ( ψ ∇ x ⃗ ⋅ a ⃗ ) = ψ ∇ x ⃗ 2 ϕ + ( ∇ x ⃗ ψ ) ⋅ ( ∇ x ⃗ ϕ ) \nabla_{\vec x} \cdot(\psi \nabla_{\vec x}\cdot \vec a)=\psi \nabla_{\vec x}^2\phi+(\nabla_{\vec x}\psi)\cdot (\nabla_{\vec x}\phi) ∇x⋅(ψ∇x⋅a)=ψ∇x2ϕ+(∇xψ)⋅(∇xϕ)

ψ \psi ψ和 ϕ \phi ϕ是标量场,以上等式由以下等式推导而来:
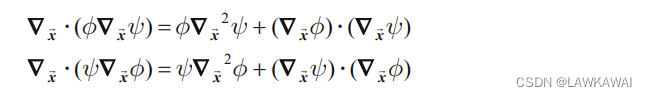
将两个等式相减,得:

保守场
一个向量场
b
⃗
(
x
⃗
,
t
)
\vec b(\vec x, t)
b(x,t)被称为保守的,如果存在一个可导的标量场
ϕ
(
x
⃗
,
t
)
\phi(\vec x, t)
ϕ(x,t),满足:
b
⃗
=
∇
x
⃗
ϕ
\vec b = \nabla_{\vec x}\phi
b=∇xϕ
如果一个函数
ϕ
\phi
ϕ满足以上关系,则称
ϕ
\phi
ϕ是
b
⃗
(
x
⃗
,
t
)
\vec b(\vec x, t)
b(x,t)的势函数。
b
⃗
(
x
⃗
,
t
)
\vec b(\vec x, t)
b(x,t)是保守的的一个不充分条件是
∇
⃗
x
⃗
∧
b
⃗
=
0
⃗
\vec \nabla_{\vec x}\wedge \vec b=\vec 0
∇x∧b=0。也就是说,给定一个保守场,其旋度
∇
⃗
x
⃗
∧
b
⃗
\vec \nabla_{\vec x}\wedge \vec b
∇x∧b等于0。反而,如果一个向量场的旋度为0,不代表这个向量场是保守的
1.46 ϕ \phi ϕ是一个标量场, u ⃗ \vec u u是一个向量场,证明 ∇ x ⃗ ⋅ ( ∇ x ⃗ ∧ v ⃗ ) = 0 \nabla_{\vec x}\cdot (\nabla_{\vec x}\wedge \vec v)=0 ∇x⋅(∇x∧v)=0以及 ∇ ⃗ x ⃗ ∧ ( ∇ x ⃗ ϕ ) = 0 ⃗ \vec \nabla_{\vec x}\wedge (\nabla_{\vec x}\phi)=\vec 0 ∇x∧(∇xϕ)=0


参考教材:
Eduardo W.V. Chaves, Notes On Continuum Mechanics