在进行路径规划时，需要获取点与点之间的距离，点之间的距离通常是通过坐标或者经纬度计算得到，可分为拟合距离和导航距离两类。导航距离顾名思义，是根据经纬度通过调用API获取，拟合距离一般是通过欧氏距离或球面距离乘以距离系数得到。

1. 常规的拟合距离

实际场景一般是大规模的（如包裹揽派可能会涉及成千上万个点），需要计算的数据量过大，而导航距离一般需要通过API获取，API的导航距离查询服务一般有查询额度限制，大量地址对的导航距离的查询非常耗时，且成本昂贵。如何能够快速高效的获取运输距离便成了一个亟待解决的问题。在大部分时候，如在点之间距离近、业务精度要求不高的时候，可以采用距离拟合的方式来计算点之间的距离。

1.1 欧氏距离

若点的位置由直角坐标系的坐标$(x,y)$表示，那么点之间的距离则为欧氏距离：
$$d_{ij}=\sqrt{(x_i-x_j{)}^2+(y_i-y_j{)}^2}$$

1. 2 球面距离拟合

由于地球可看作一个球体，假设地球半径为$R$(6378.137km)，那么可以计算得到点之间的球面距离，并乘以一个距离系数$k$，得到拟合的运输距离：
$$\begin{gathered} radLa{t}_i=\frac{la{t}_i\ast \pi }{180},radLa{t}_j=\frac{la{t}_j\ast \pi }{180} \\ dif{f}_1=radLa{t}_i-radLa{t}_j \\ dif{f}_2=\frac{lo{n}_i\ast \pi }{180}-\frac{lo{n}_j\ast \pi }{180} \\ {d}_{ij}=k\ast 2R\ast arcsin\sqrt{si{n}^2(\frac{dif{f}_1}{2})+cos(radLa{t}_i)cos(radLa{t}_j)si{n}^2(\frac{dif{f}_2}{2})} \end{gathered}$$
一般而言，由于不同的规划场景道路状况不同，距离系数$k$会根据规划的场景变化。

2. 一种改进的球面距离拟合

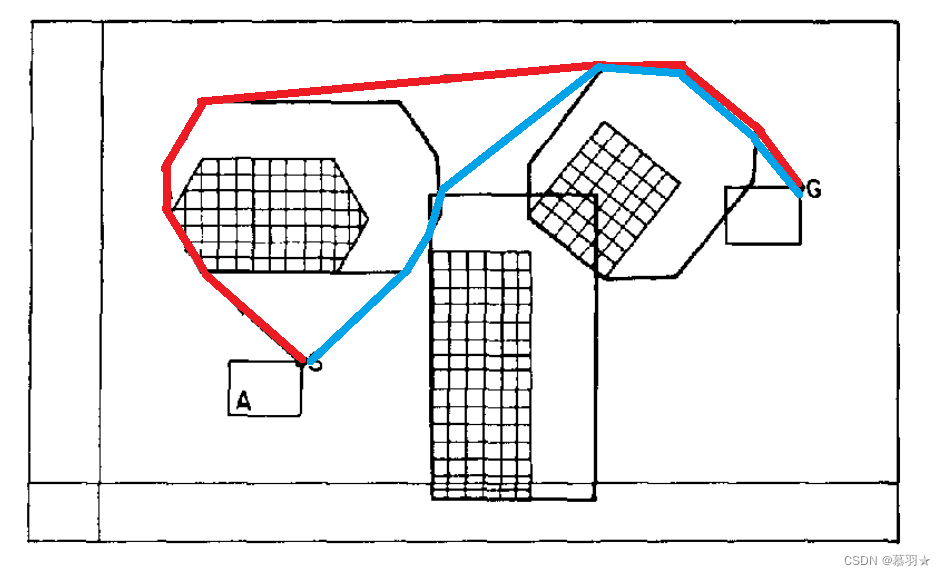
在业务中，若点之间距离过远，或涉及到需要落地的场景，常规的拟合运输距离可能会存在误差过大的情况。而考虑到导航距离获取的难度，为了进一步提升球面距离的拟合精度，Radu等人[1]提出了一种新的运输距离拟合的方法。
首先从需要规划的点中进行采样出$n$个点，计算这$n$个点之间的导航距离和球面这里，然后可以得到点与点之间的距离系数$k_{i,j}$。在计算其他节点之间$(A,B)$的距离时，首先通过球面距离，找到分别离这两个节点最近的采样点$NN(A)$、$NN(B)$，采用最近采样点之间的距离系数$k_{NN(A)NN(B)}$作为节点$(A,B)$之间的距离系数，然后计算节点$(A,B)$之间的拟合运输距离。

图1 采样点示例（左图橘色为实际运输距离，蓝色为球面距离； 右图为计算得到的点之间的距离系数）

图2 非采样点之间的运输距离拟合 该方法的准确性取决于两个因素：图的大小和节点的位置。 增加采样节点的数量会减少到节点的平均距离，从而提高距离估计的准确性。 但是，大图需要更多内存并且会减慢该方法的速度。 注：这种方法在平原会更有效，如果规划城市为像重庆这种的魔幻3D城市，那么这种方法并不适用。

参考文献

[1] Radu Mariescu-Istodor and Pasi Fr.nti. 2021. Fast travel-distance estimation using overhead graph. Journal of Location Based Services (2021), 1-19.