C# KMeans聚类算法的实现

前言

本章分享一下如何使用C#实现KMeans算法。在讲解代码前先清晰两个小问题：

1. 什么是聚类?
   聚类是将数据点根据其相似性分组的过程，它有很多的应用场景，比如：图像分割、文本分类、推荐系统等等。在这些应用场景里面我们需要将数据点分成多个簇，每个簇内的数据点具有相似的特征，以便于我们能够更简单的处理数据。

2. 什么是KMeans?
   KMeans算法是一种常用的聚类算法，它可以将数据点分组成具有相似特征的簇。

示例代码

话不多说，我们直接上代码：

    /// <summary>
    /// KMeans算法类
    /// </summary>
    public static class KMeans
    {
        /// <summary>
        /// 使用 KMeans 算法对 Point 数组进行聚类
        /// </summary>
        /// <param name="points">待聚类的 Point 数组</param>
        /// <param name="k">聚类的个数</param>
        /// <returns>聚类的结果</returns>
        public static List<List<PointD>> Cluster(PointD[] points, int k)
        {
            // 初始化簇心的位置
            Random random = new Random();
            PointD[] centroids = new PointD[k];
            for (int i = 0; i < k; i++)
            {
                centroids[i] = points[random.Next(points.Length)];
            }

            // 分配每个点到最近的簇心
            List<PointD>[] clusters = new List<PointD>[k];
            for (int i = 0; i < k; i++)
            {
                clusters[i] = new List<PointD>();
            }

            foreach (PointD point in points)
            {
                int closest = 0;
                var closestDistance = Distance(point, centroids[0]);
                for (int i = 1; i < k; i++)
                {
                    var distance = Distance(point, centroids[i]);
                    if (distance < closestDistance)
                    {
                        closest = i;
                        closestDistance = distance;
                    }
                }
                clusters[closest].Add(point);
            }

            // 重新计算簇心位置
            bool moved = true;
            while (moved)
            {
                moved = false;
                for (int i = 0; i < k; i++)
                {
                    PointD newCentroid = Centroid(clusters[i]);
                    if (!newCentroid.Equals(centroids[i]))
                    {
                        centroids[i] = newCentroid;
                        moved = true;
                    }
                }
                if (moved)
                {
                    // 重新分配每个点到最近的簇心
                    for (int i = 0; i < k; i++)
                    {
                        clusters[i].Clear();
                    }
                    foreach (PointD point in points)
                    {
                        int closest = 0;
                        var closestDistance = Distance(point, centroids[0]);
                        for (int i = 1; i < k; i++)
                        {
                            var distance = Distance(point, centroids[i]);
                            if (distance < closestDistance)
                            {
                                closest = i;
                                closestDistance = distance;
                            }
                        }
                        clusters[closest].Add(point);
                    }
                }
            }

            // 返回每个簇的点集合
            List<List<PointD>> result = new List<List<PointD>>();
            for (int i = 0; i < k; i++)
            {
                result.Add(clusters[i]);
            }
            return result;
        }

        private static double Distance(PointD a, PointD b)
        {
            var dx = a.X - b.X;
            var dy = a.Y - b.Y;
            return Math.Sqrt(dx * dx + dy * dy);
        }

        private static PointD Centroid(List<PointD> points)
        {
            double totalX = 0;
            double totalY = 0;
            foreach (PointD point in points)
            {
                totalX += point.X;
                totalY += point.Y;
            }
            var centerX = totalX / points.Count;
            var centerY = totalY / points.Count;
            return new PointD(centerX, centerY);
        }
    }

我们这里定义了一个双进度点的结构体PointD:

    public struct PointD 
    {
        public PointD(double x, double y) 
        {
            X = x;
            Y = y;
        }

        public double X { get; set; }
        public double Y { get; set; }

        public override bool Equals(object obj)
        {
            if (obj == null || GetType() != obj.GetType())
            {
                return false;
            }

            PointD other = (PointD)obj;
            return X.Equals(other.X) && Y.Equals(other.Y);
        }
    }

实现思路

接下来详细讲解一下KMeans算法的思路。

KMeans类中包含名为Cluster的静态方法。该方法接收两个参数，【待聚类的Point数组】和【聚类的个数】。

第一步是要随机初始化簇心的位置（使用Random）。

第二步要将每个数据点分配到距离其最近的簇心中。思路是：对于每个数据点都计算其与所有簇心的距离（使用名为Distance的私有静态方法），找到最近的簇心，并将该数据点分配到该簇中。

第三步要重新计算每个簇心的位置（使用静态方法Centroid）。每个簇都计算其所有数据点的中心点作为该簇的新簇心。如果新簇心和旧簇心不同，则说明簇心已经发生了移动，我们需要重新分配每个数据点到距离其最近的簇心中。

第四步返回聚类结果，也就是每个簇内的数据点集合。

由于我们在第一步的时候就是用的Random来随机选择初始簇心，因此多次聚类的结果可能不一样。

测试结果

测试代码如下：

    [TestClass]
    public class KMeansTest
    {
        [TestMethod]
        public void TestCluster()
        {
            PointD[] points = new PointD[]
            {
                new PointD(1, 2),
                new PointD(2, 1),
                new PointD(3, 2),
                new PointD(2, 3),
                new PointD(5, 6),
                new PointD(6, 5),
                new PointD(7, 6),
                new PointD(6, 7),
            };
            int k = 3;
            List<List<PointD>> clusters = KMeans.Cluster(points, k);
            foreach (List<PointD> cluster in clusters)
            {
                Console.WriteLine("Cluster:");
                foreach (PointD point in cluster)
                {
                    Console.WriteLine("  ({0}, {1})", point.X, point.Y);
                }
            }
        }
    }

连续三次执行的结果如下：

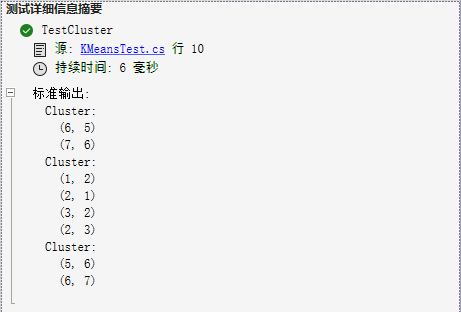
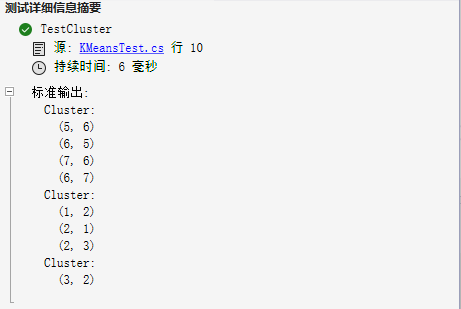
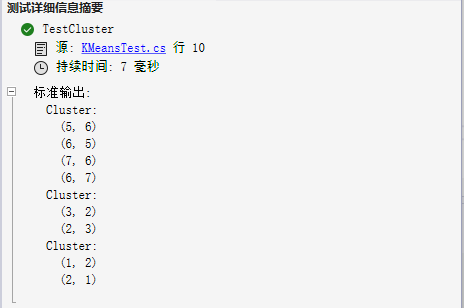
结束语

通过本章的代码可以轻松实现KMeans算法对数据聚类。如果您觉得本文对您有所帮助，请不要吝啬您的点赞和评论，提供宝贵的反馈和建议，让更多的读者受益。