前言

        首先需要指明本文中描述的R,G,B并非通常的sRGB中的三个分量R',G',B'，而是波长分别为700nm，546.1nm，435.8nm的单色红光，单色绿光，单色蓝光。sRGB中的R'G'B'中的红色、绿色、蓝色已经不是单色光了。虽然习惯上大家都叫RGB，但是需要有所区别。本文将分别从为什么需要这种转换，怎么进行这种转换进行阐述。

为什么需要XYZ色彩空间？

        为什么需要从RGB映射到XYZ色彩空间，一句话表述就是因为方便计算。这样回答似乎太过简单，但是事实确实如此，详细原因需要回顾一下混色的原理。

1，色匹配实验

        

        上式中的加号表达的是组合之意，而非数学上的相加。式子右侧部分RGB是三种单色刺激色，rgb表示的是相对系数。

        

        

        

 对于可见光依次测量各个波长的三色刺激值，那么可以得到如下：

         

         

         

         

         

特别的当波长处于三基色波长时有如下：

        

波长（nm）	r	g	b
700	1	0	0
546.1	0	1	0
435.8	0	0	1

将所录的数据使用图形表达出来，可以看到部分波长期间，R分量出现了负值：

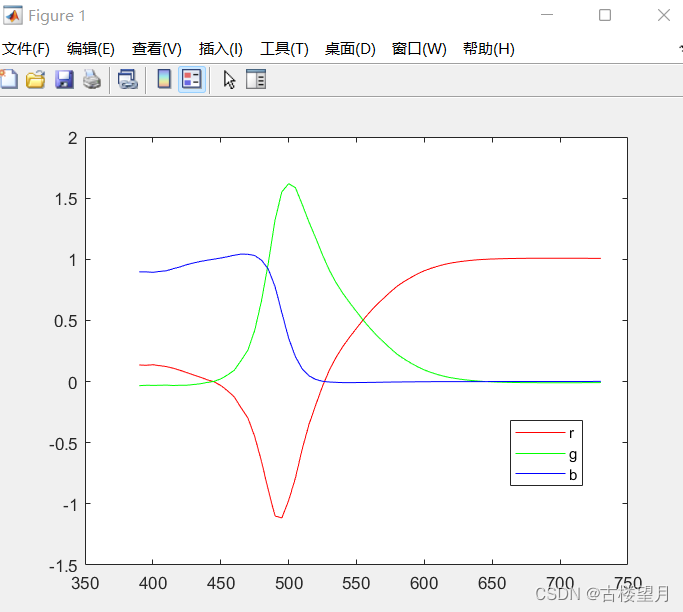
 代码如下：        

wave=csvread('./cie data/cie_rgb_5nm.csv',0,0,[0,0,68,0]);
R=csvread('./cie data/cie_rgb_5nm.csv',0,1,[0,1,68,1]);
G=csvread('./cie data/cie_rgb_5nm.csv',0,2,[0,2,68,2]);
B=csvread('./cie data/cie_rgb_5nm.csv',0,3,[0,3,68,3]);
r=R./(R+G+B);
g=G./(R+G+B);
b=B./(R+G+B);
figure
plot(wave,r,'r');hold on
plot(wave,g,'g');hold on
plot(wave,b,'b');hold on
legend('r','g','b','Location','east');

2，混色原理

更一般的表达，应该在式子的左右乘以功率系数：

    

其中功率有如下关系：

        

实际做实验的过程中，保持功率不变，所以：

        

假定现在有一束连续的光，连续的意思代表是光谱连续分布,设连续光的功率分布如下：

        

那么相对于色匹配实验的功率之比为：

        

因此这束光的颜色可以用下面的表达式描述：

        

       

        

        

 简单起见，如果这束光是离散的2个频点，那么就用求和的形式表达：