文章目录
- logisim的使用
- 1.添加门电路
- 2.添加引脚
- 3.添加导线
- 4.添加文本
- 5.测试电路
- 补充工具
- 实验一,运算器实验
- 8位串行可控加减法器
- 分析一位全加器
- 八位串行加法器即可给出
- 8位串行可控加减法器
- 回答问题
- CLA74182(先行进位加法器)
- 参数
- 公式
- 问题
- 位快速加法器
- 16位快速加法器
- 32位快速加法器
- ALU
- 实现功能
logisim的使用
1.添加门电路
点击资源栏-Gates选项中的门电路,即可在右边画布添加
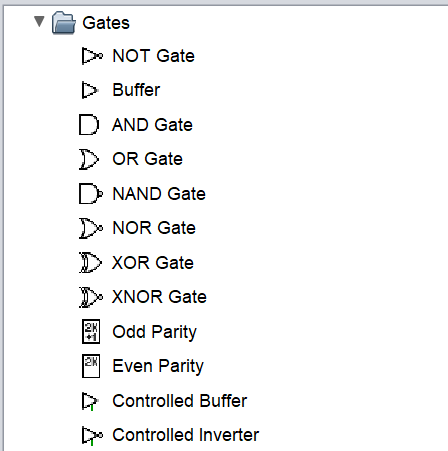
添加成功后如下:
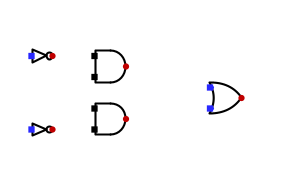
2.添加引脚
引脚可在菜单栏中找到

也可在资源栏-Wiring中找到
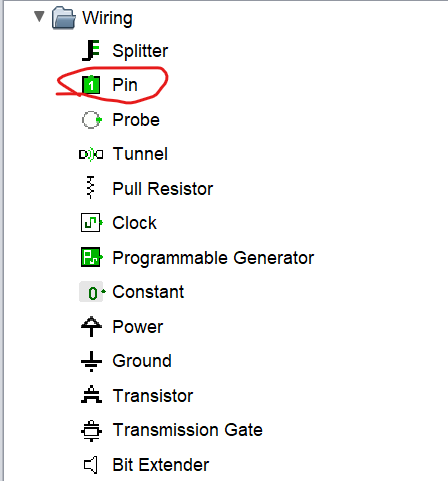
添加入画板后,可在属性表中修改面向方向
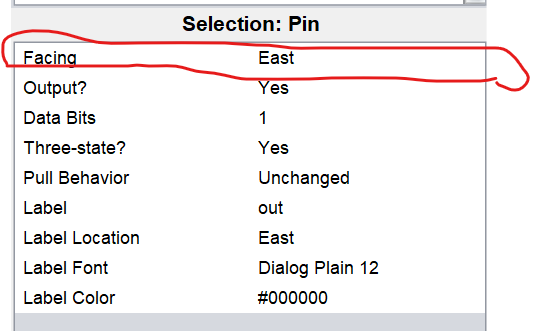
最后得到如下图
注:方形为输出,圆形为输入。
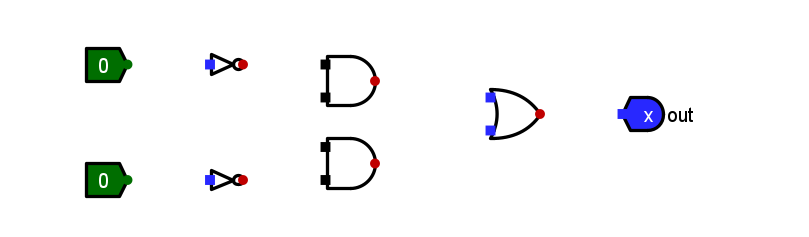
3.添加导线
使用光标连接两个结点即可
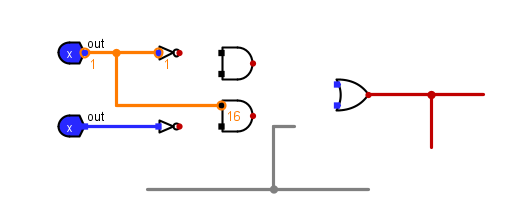
- 灰色:线的位宽未知。发生这种情况是因为导线未连接到任何组件的输入和输出。(所有输入和输出都有一个定义的位宽。)
- 蓝色:导线带有一位值,但没有任何东西将特定值驱动到导线上。我们称之为浮动位; 有人称之为高阻抗值。在此示例中,将值放置到导线上的组件是三态引脚,因此它可以发出此浮动值。深绿色:电线带有一位0值。
- 亮绿色:导线带有一位1值。
- 黑色:电线带有多位值。可能未指定部分或全部位。
- 红色:电线带有错误值。这通常是因为门无法确定正确的输出,可能是因为它没有输入。它也可能因为两个组件试图将不同的值发送到线路上而产生; 这就是上面的例子中发生的情况,其中一个输入引脚将0置于线上,而另一个输入引脚将1置于同一线上,从而导致冲突。当任何携带的位是错误值时,多位线将变为红色。
- 橙色:连接到导线的元件的位宽不一致。橙色线有效地“断开”:它不承载组件之间的值。在这里,我们将一个两位组件附加到一位组件,因此它们是不兼容的。
若出现橙色线缆,修改门电路的Data Bits值,使之组件位数一致。
连接完成后,电缆都为绿色,表示连接完成。
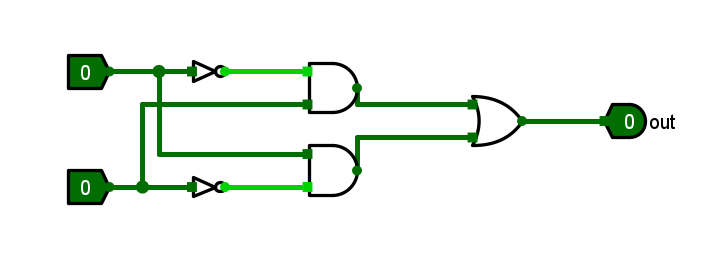
4.添加文本
选择文本工具
点击引脚,输入标签。对引脚注释
或点击任意未知,进行注释。
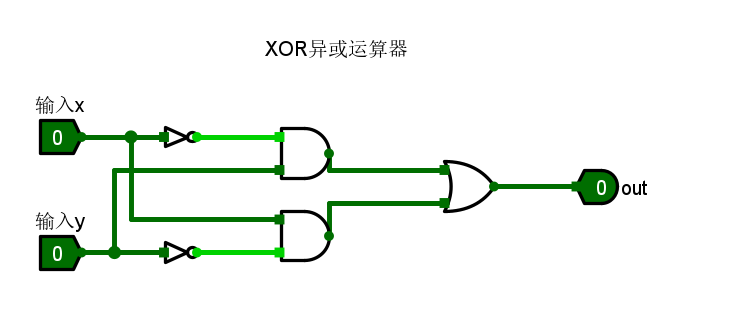
5.测试电路
选择戳工具 ,点击输入引脚,即可改变它的输入值。
,点击输入引脚,即可改变它的输入值。
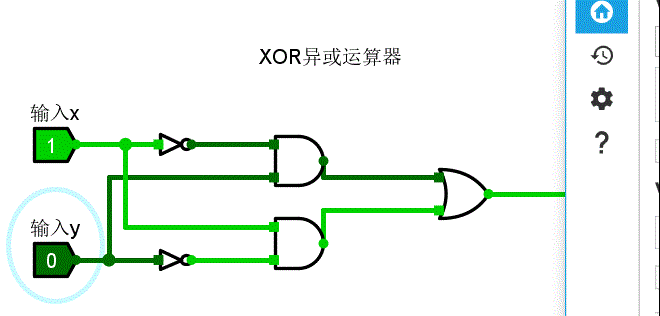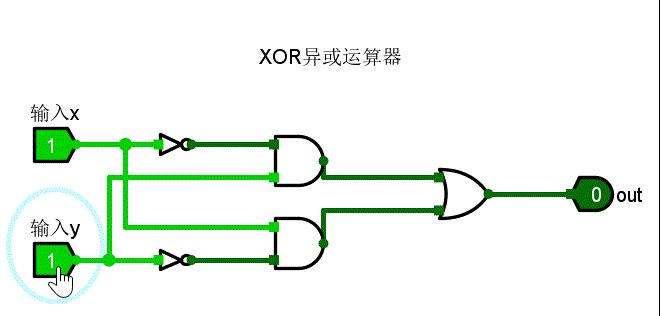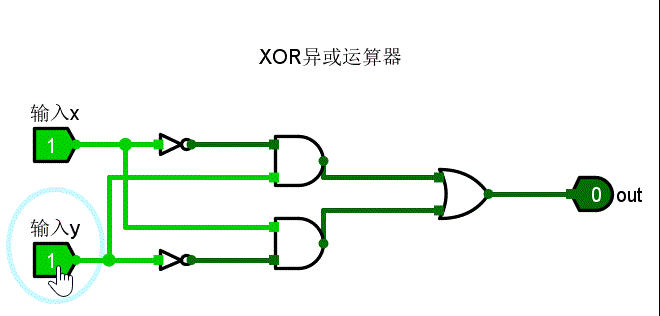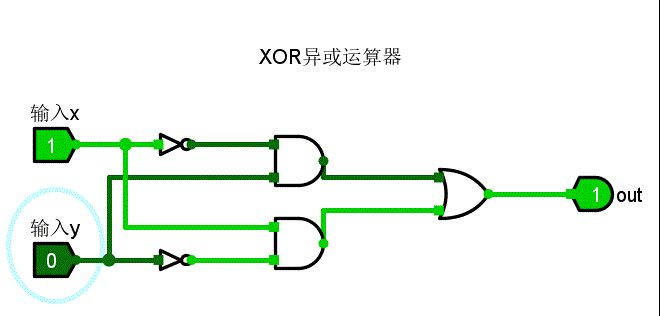
可以看到,当线缆表示1时,为亮绿色;线缆表示0时,为深绿色。
补充工具

实验一,运算器实验
同学们需要在视频中对于你所实现的8位串行可控加减法器,CLA74182,4位快速加法器,16位快速加法器,32位快速加法器以及ALU的进行介绍并回答相应问题。
- 依次比照你所实现的各个电路,口述你对该电路的实现思路以及你是如何从头构建起这个电路并使其正常工作的。
- 对于每一个电路,你可以回顾并介绍你在实现该电路过程中遇到的问题,以及你是如何解决这个问题的(加分项)
- 此外,我们对每个电路,也都准备了相应的问题和演示要求,同学们在视频演示中演示到了相应的电路时,除了上述两条,还需要在视频中对如下问题进行回答。同学们如果不知道从什么角度来介绍电路,也可以从这些问题中获得思路启发。
8位串行可控加减法器
- 对于加减法的控制,你是采取何种方式实现的?
- 你是怎样实现溢出检测的?其数学原理是什么?
分析一位全加器
书 P 65 P_{65} P65
设输入为x,y,进位为c。
则该位为x^y^c
进位当且仅当x,y都为1,或z为1,且x,y有一个为1。用符号表示为
(x&y) | (x^y)&z
用电路表示为
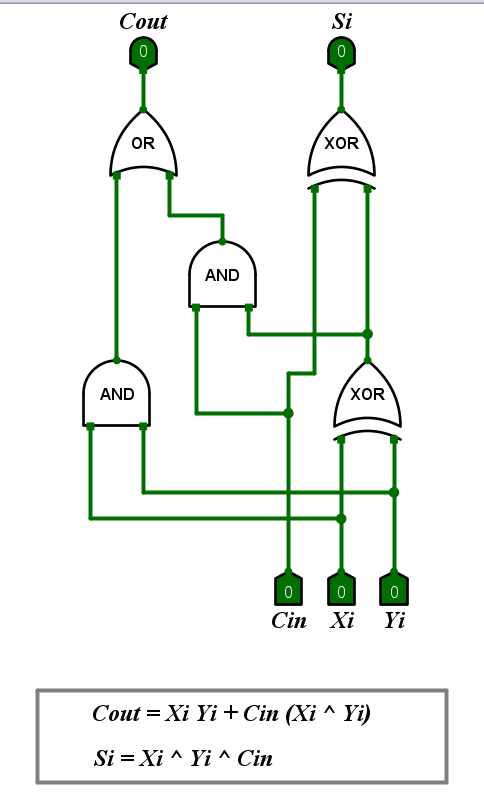
已在一位全加器FA中给出。
八位串行加法器即可给出
书
P
65
P_{65}
P65
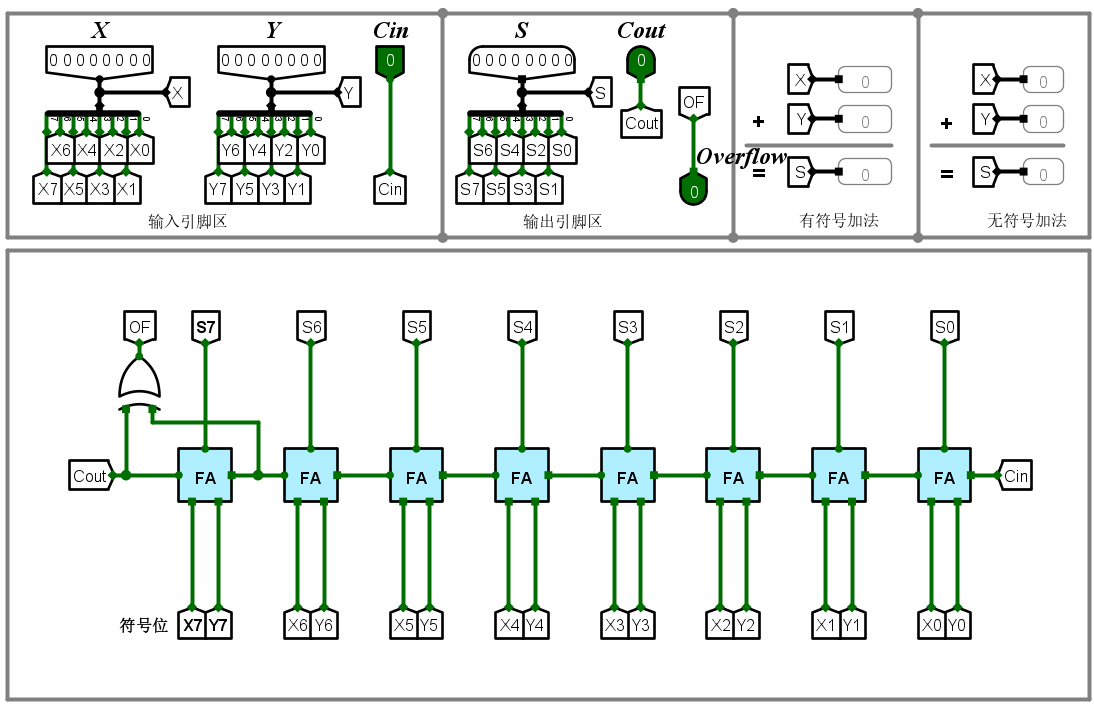
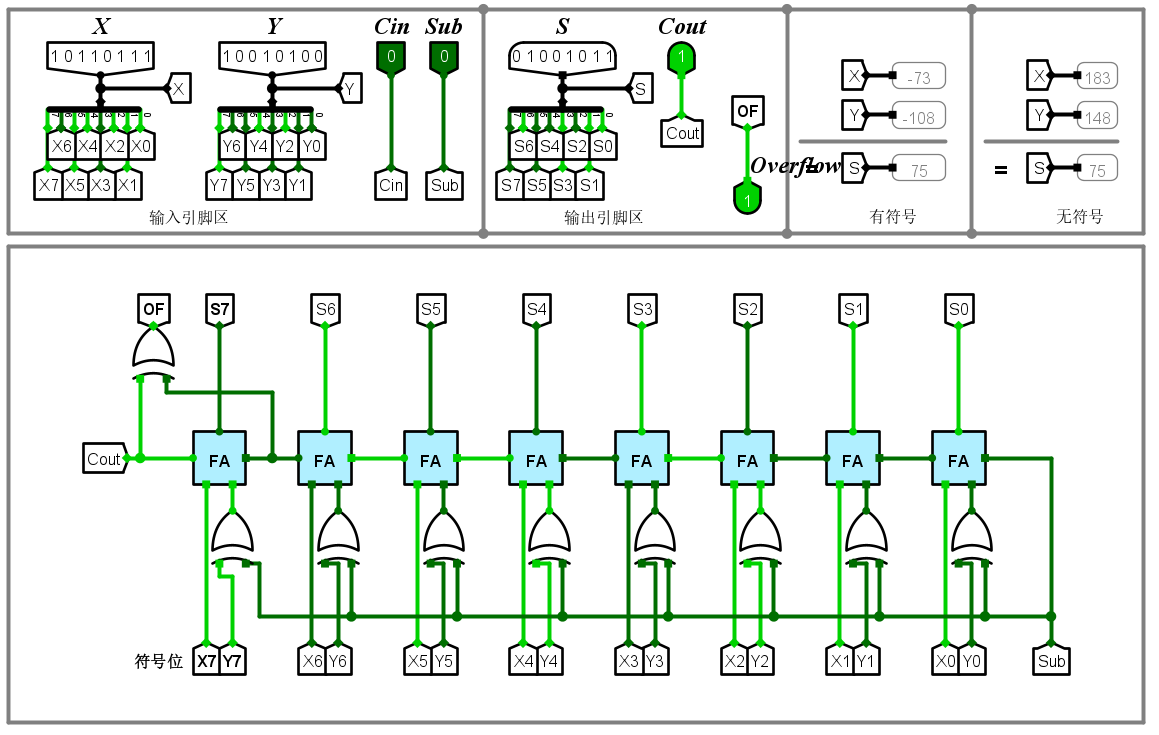
8位串行可控加减法器
书 P 66 P_{66} P66
在8为串行加法器的基础上加入可控符号Sign,若为减法,将y的补码修改为(-y)的补码(取反+1)。
若有
S
补
=
x
补
−
y
补
S_补 = x_补 - y_补
S补=x补−y补,即有
S
补
=
x
补
+
(
反
码
(
y
补
)
+
1
)
=
(
x
补
+
反
码
(
y
补
)
)
+
1
S_补 = x_补 + (反码(y_补)+1) = (x_补 + 反码(y_补)) + 1
S补=x补+(反码(y补)+1)=(x补+反码(y补))+1;
可将最低为的Cin设为1,当作减法计算中反码加1的操作。
Sub为1时,y取反;Sub为0时,y不变。有-y = y^Sub
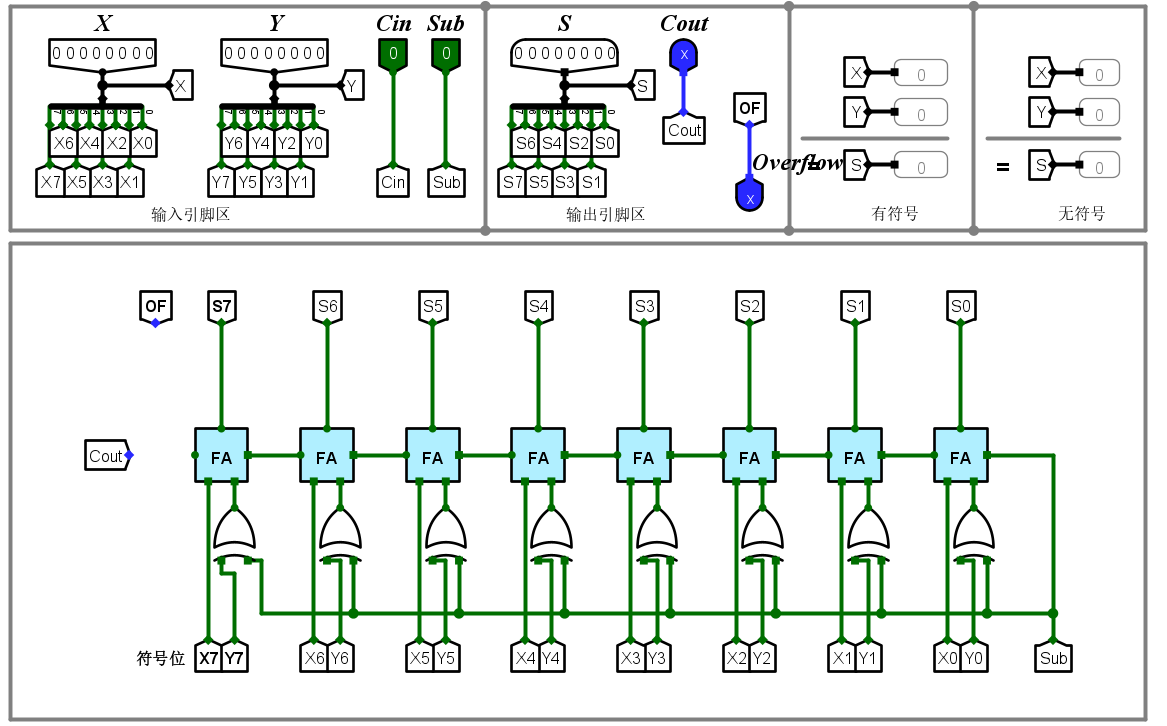
对于OF溢出,检测方法有两种:
- 根据操作数和运算结果的符号位是否一致进行检测(负负得正,正正得负时溢出),
S
f
S_f
Sf为运算结果的符号位
O F = X f Y f S f ‾ + X f ‾ Y f ‾ S f OF = X_fY_f\overline{S_f} + \overline{X_f}\ \overline{Y_f}S_f OF=XfYfSf+Xf YfSf - 根据运算时最高数据位产生的进位信号
C
d
C_d
Cd,符号位产生的进位信号
C
f
C_f
Cf判断,当两个进位不一致时溢出
O F = C f ⊕ C d OF = C_f \oplus C_d OF=Cf⊕Cd
显然方法二更容易实现。
对于无符号溢出,Cout为1即可判断溢出。
回答问题
-
对于加减法的控制,你是采取何种方式实现的?
当Sub为1时,y取反,且在最低位加法器有进位1;
当Sub为0时,y不变。
有 − y = y ⊕ S u b -y = y \oplus Sub −y=y⊕Sub。
将Sub作为最低一位加法器的进位,Sub=1时,与y的每一位作异或运算。 -
你是怎样实现溢出检测的?其数学原理是什么?
根据运算时最高数据位产生的进位信号 C d C_d Cd,符号位产生的进位信号 C f C_f Cf判断,当两个进位不一致时溢出,有
O F = C f ⊕ C d OF = C_f \oplus C_d OF=Cf⊕Cd
CLA74182(先行进位加法器)
书 P 67 P_{67} P67
- CLA74182的作⽤是什么?
参数
低位进位
C
0
C_0
C0
产生进位
C
i
C_i
Ci
进位生成函数
G
i
G_i
Gi
进位传递函数
P
i
P_i
Pi
成组进位生成函数
G
∗
G^*
G∗
成组进位传递函数
P
∗
P^*
P∗
公式
S
i
=
P
i
⊕
C
i
C
i
+
1
=
G
i
+
P
i
C
i
⇒
C
1
=
G
0
+
P
0
C
0
⇒
C
2
=
G
1
+
P
1
C
1
=
G
1
+
P
1
G
0
+
P
1
P
0
C
0
⇒
C
3
=
G
2
+
P
2
G
1
+
P
2
P
1
G
0
+
P
2
P
1
P
0
C
0
⇒
以
此
类
推
S_i = P_i \oplus C_i \\ C_{i+1} = G_i + P_iC_i \\ \quad\\ \Rightarrow C_1 = G_0 + P_0C_0 \\ \Rightarrow C_2 = G_1 + P_1C_1 = G_1 + P_1G_0 + P_1P_0C_0\\ \Rightarrow C_3 = G_2+P_2G_1+P_2P_1G_0+P_2P_1P_0C_0 \\ \Rightarrow 以此类推
Si=Pi⊕CiCi+1=Gi+PiCi⇒C1=G0+P0C0⇒C2=G1+P1C1=G1+P1G0+P1P0C0⇒C3=G2+P2G1+P2P1G0+P2P1P0C0⇒以此类推
G
∗
=
G
3
+
P
3
G
2
+
P
3
P
2
G
1
+
P
3
P
2
P
1
G
0
P
∗
=
P
3
P
2
P
1
P
0
G^* = G_3+P_3G_2+P_3P_2G_1+P_3P_2P_1G_0 \\ P_* = P_3P_2P_1P_0
G∗=G3+P3G2+P3P2G1+P3P2P1G0P∗=P3P2P1P0
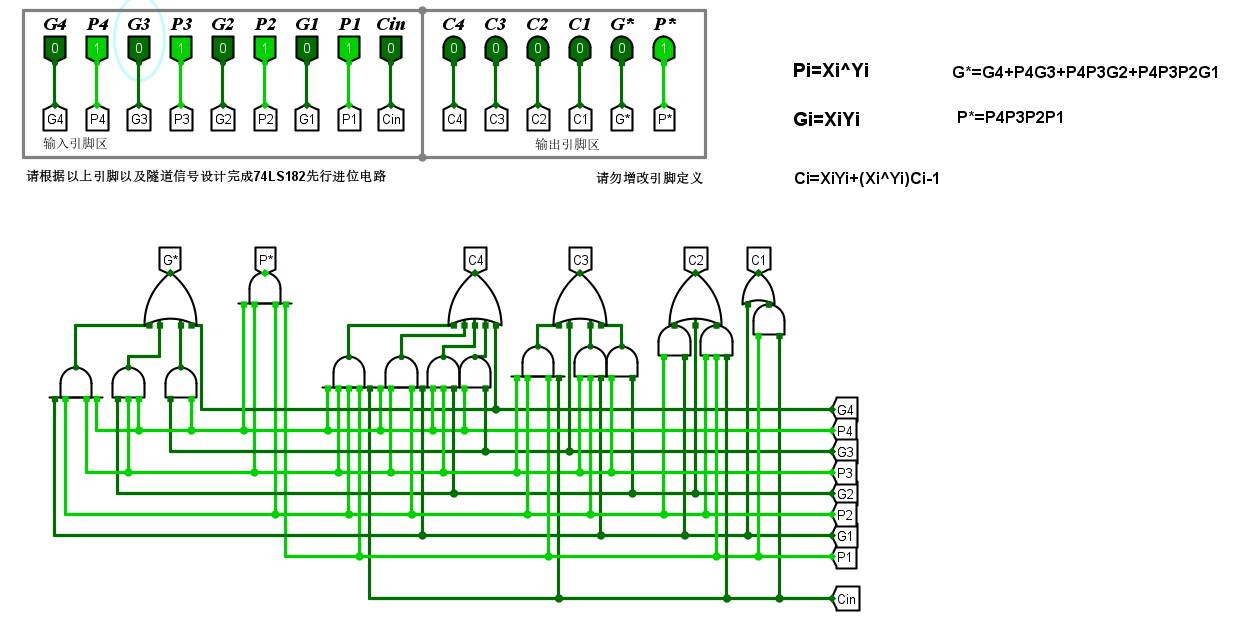
问题
- CLA74182的作⽤是什么?
提前得到所有全加器所需的进位输入信号,所有全加器都可以并行计算从而提高运算性能。
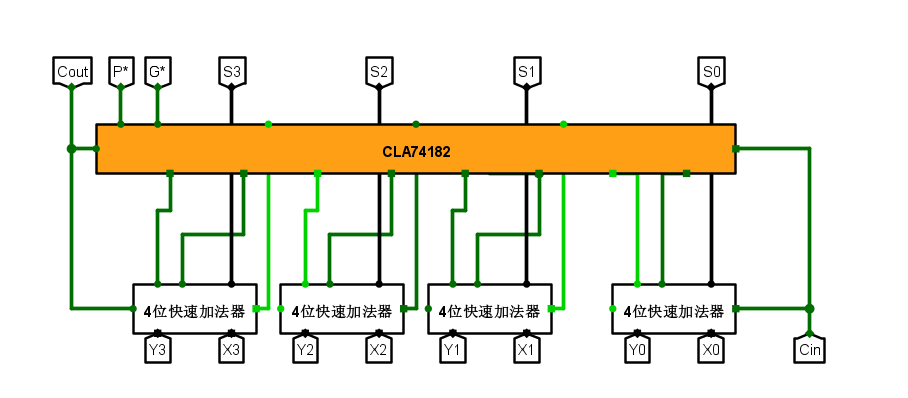
位快速加法器
- 快速加法器与普通的串⾏加法器的区别是什么?他是通过什么⽅法来实现“快速”的?
16位快速加法器
32位快速加法器
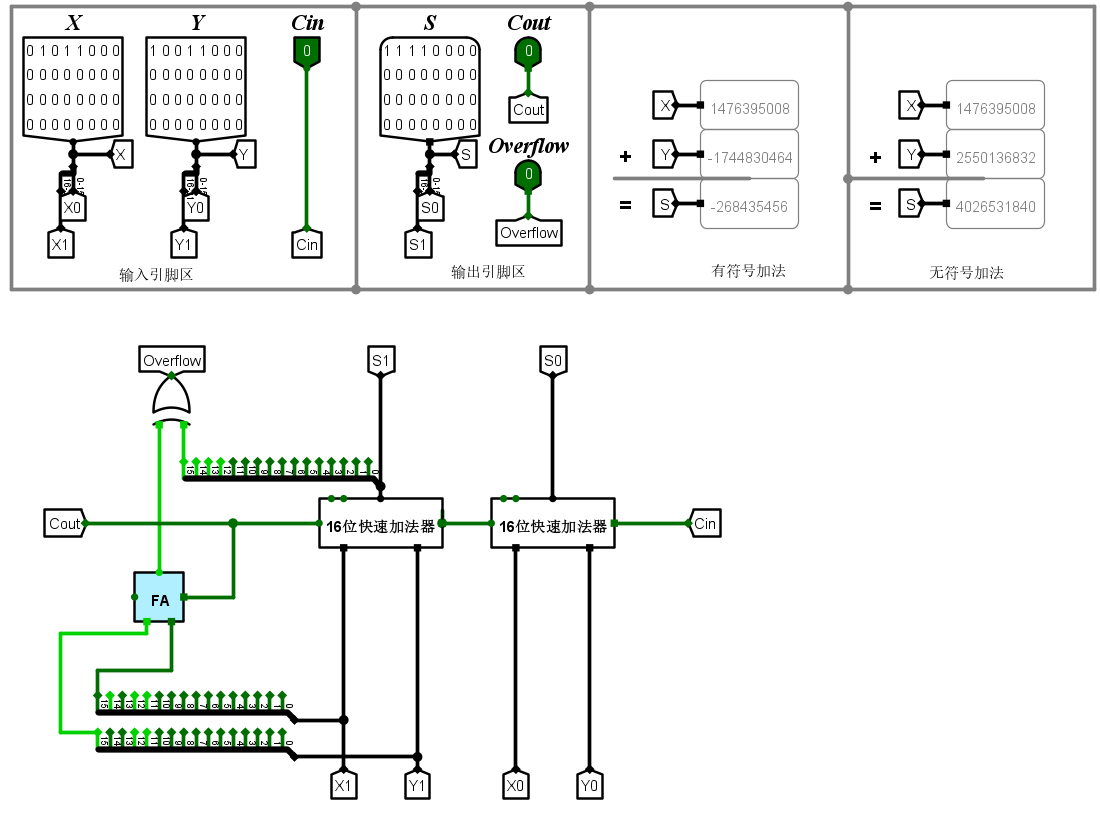
- 你的溢出检测是如何实现的?这⾥是否可以选择其他的溢出检测⽅法?
使用利用变形补码的符号位进行检测。 - 实现此电路有哪些值得注意的地⽅?
ALU
根据已有工具构造

实现功能
| ALU OP | 十进制 | 运算功能 |
|---|---|---|
| 0000 | 0 | Result = X << Y 逻辑左移(Y 取低五位)Result2=0 |
| 0001 | 1 | Result = X >>>Y 算术右移(Y 取低五位)Result2=0 |
| 0010 | 2 | Result = X >> Y 逻辑右移(Y 取低五位)Result2=0 |
| 0011 | 3 | Result = (X * Y)[31:0]; Result2 = (X * Y)[63:32] 有符号 |
| 0100 | 4 | Result = X/Y; Result2 = X%Y 无符号 |
| 0101 | 5 | Result = X + Y (Set OF/UOF) |
| 0110 | 6 | Result = X - Y (Set OF/UOF) |
| 0111 | 7 | Result = X & Y 按位与 |
| 1000 | 8 | Result = X | Y 按位或 |
| 1001 | 9 | Result = X⊕Y 按位异或 |
| 1010 | 10 | Result = ~(X |Y) 按位或非 |
| 1011 | 11 | Result = (X < Y) ? 1 : 0 符号比较 |
| 1100 | 12 | Result = (X < Y) ? 1 : 0 无符号比较 |
有关运算器的使用可参考:Logisim元件用法详解四:Arithmetic 运算器
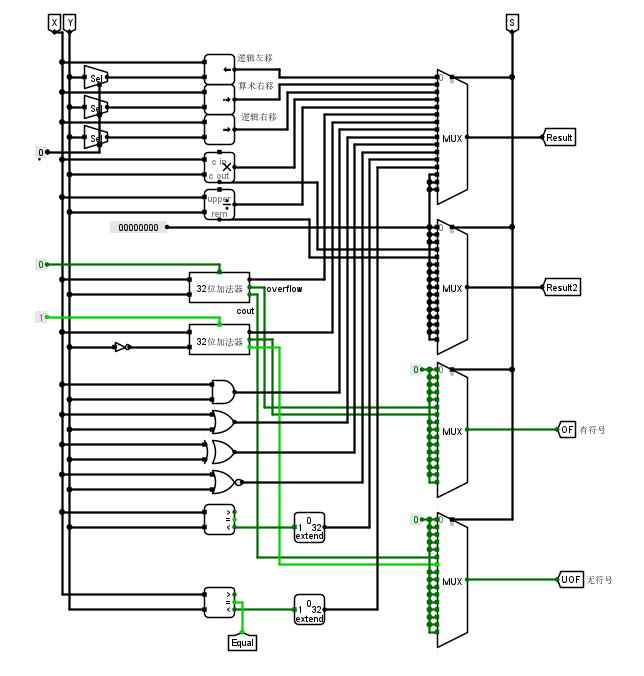
- 怎样实现功能选择?
- 依次介绍各个功能的实现⽅式
- 重点介绍OF,UOF,加法,减法
- 运⾏运算器测试电路检测

![[附源码]计算机毕业设计springboot校园商铺](https://img-blog.csdnimg.cn/80f868d4a3a346158e29165ac1ef8984.png)
![[附源码]Python计算机毕业设计Django基于web的羽毛球管理系统](https://img-blog.csdnimg.cn/162d3968520145bd9d5d26d0fbb8319a.png)