误差的来源是多方面的,但主要来源为:过失误差,描述误差,观测误差,截断误差和舍入误差。
过失误差
过失误差是由设备故障和人为的错误所产生的误差,在由于每个人都有“权利”利用机器进行数值计算,所以在计算方法研究领域应当强调怎样有效避免过失误差。
我们的计算方法对于如何消除描述误差,观测误差和舍入误差无能为力,但是应当考虑尽量消除这些误差对计算结果的影响,也就是减少误差的传播。
截断误差
定义:假如真值x* 为近似值系列{xn}的极限,由于计算机只能执行有限步的计算过程,所以我们只能选取某个xN作为x *的近似值,由此产生的误差称为截断误差。
⚠️注意:由于非初等函数值的计算在很多情况下要用到逼近法或迭代法,都与取极限有关,所以对截断误差的分析在计算方法课中有特别重要的地位。
对任意一个极限过程,我们总可以构造一个相应的无穷级数。比如:若an→a,则
![]()
所以,我们总可以把截断误差理解为一个无穷级数,特别是函数的泰勒展式,的余项。
利用泰勒展开式来说明截断误差

注释:泰勒展开式前n+1项为fn(x),剩下的项为Rn(x)。我们一般只使用前n+1项,会舍去后面的其余项,此时Rn(x)的值就是截断误差。
描述误差
为了便于数学分析和数值计算,人们对实际问题的数学描述通常只反映出主要因素之间的数量关系,而忽略次要因素的作用,由此产生的误差称为描述误差。
举例:假设一门大炮的炮筒与水平面的夹角为θ,所发射的炮弹的出口速度为v0,那么t秒钟后炮弹的位置可表示为
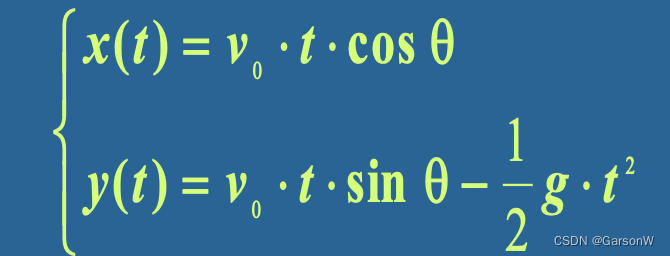
在这个模型中,我们忽略了空气的阻力。
对实际问题进行数学描述通常称为是建立数学模型,所以描述误差也称为是模型误差。
观测误差
定义:描述实际问题或实际系统的数学模型中的某些参数往往是通过实验观测得到的。由试验得到的数据与实际数据之间的误差称为观测误差。
举例:在上面的描述炮弹运动方程的数学模型中,我们用到了重力加速度g,它在地球表面的不同位置以及不同高度的值是不同的,我们可以通过实验测出它的近似值,但无法得到它的准确值,所以求解具体问题时,就避免不了观测误差。
提示:我们平时用仪表测量电压、电流、压力、温度时,指针通常会落在两个刻度之间,所以读数的最后一位只能是估计值,从而也产生了观测误差。即使是一些高精密度的数字化仪表,所显示出来的测量结果的最后一位数字是不可靠的。
舍入误差
几乎所有的计算工具,当然也包括电子计算机,都只能用一定数位的小数来近似地表示数位较多或无限的小数,由此产生的误差称为舍入误差。
我们可以作一个小试验来感受由于计算工具的局限性所产生的舍入误差:编一个最简单的C语言程序,定义单精度浮点型变量X,设初值为0.123456789,再用9位小数的形式显示出来,我们会发现,输入的数和输出的数之间存在误差,这就是舍入误差。
⚠️提示:过去的计算工具落后,所以舍入误差也较大,现在我们在计算机上用双精度浮点数计算,可以得到15位有效数字,这是以前很难达到的精度。

![[CTF/网络安全] 攻防世界 ics-06 解题详析](https://img-blog.csdnimg.cn/997f986390514d219ef2b058037947b0.png#pic_center)