一文详解Pytorch中的Tensor操作

news2024/11/17 23:26:00

何为Tensor？

Tensor的英文原义是张量，PyTorch官网对其的定义如下：

在这里插入图片描述

也就是说，一个Tensor是一个包含单一数据类型的多维矩阵。通常，其多维特性用三维及以上的矩阵来描述，例如下图所示：单个元素为标量(scalar)，一个序列为向量(vector)，多个序列组成的平面为矩阵(matrix)，多个平面组成的立方体为张量（tensor）。

在这里插入图片描述

当然，张量也无需严格限制在三维及以上。在深度学习的范畴内，标量、向量和矩阵也可分为称为0维张量、一维张量、二维张量。

为什么需要Tensor?

熟悉机器学习的小伙伴们应该都知道，有监督机器学习模型的输入X通常是多个特征列组成的二维矩阵，输出y是单个特征列组成的标签向量或多个特征列组成的二维矩阵。那么深度学习中，为何要定义多维矩阵Tensor呢？

深度学习当前最成熟的两大应用方向莫过于CV和NLP，其中CV面向图像和视频，NLP面向语音和文本，二者分别以卷积神经网络和循环神经网络作为核心基础模块，且标准输入数据集都是至少三维以上。其中，

  • 图像数据集：至少包含三个维度（样本数Nx图像高度Hx图像宽度W）；如果是彩色图像，则还需增加一个通道C，包含四个维度（NxHxWxC）；如果是视频帧，可能还需要增加一个维度T，表示将视频划分为T个等时长的片段。
  • 文本数据集：包含三个维度(样本数N×序列长度L×特征数H)。

因此，输入学习模型的输入数据结构通常都要三维以上，这也就促使了Tensor的诞生。

Tensor属性

Tensor形状

张量具有如下形状属性：

  • Tensor.ndim：张量的维度，例如向量的维度为1，矩阵的维度为2。
  • Tensor.shape： 张量每个维度上元素的数量。
  • Tensor.shape[n]：张量第n维的大小。第n维也称为轴（axis）。
  • Tensor.numel：张量中全部元素的个数。

如下是创建一个四维Tensor，并通过图形直观表达以上几个概念的关系。

import torch
Tensor=torch.ones([2,3,4,5])
print("Number of dimensions:", Tensor.ndim)
print("Shape of Tensor:", Tensor.shape)
print("Elements number along axis 0 of Tensor:", Tensor.shape[0])
print("Elements number along the last axis of Tensor:", Tensor.shape[-1])
print('Number of elements in Tensor: ', Tensor.numel())  #用.numel表示元素个数

在这里插入图片描述

Tensor的axis、shape、dimension、ndim之间的关系如下图所示。

在这里插入图片描述

Tensor数据类型

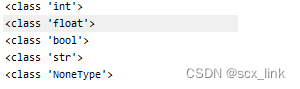
torch.dtype属性标识了torch.Tensor的数据类型。PyTorch有八种不同的数据类型：

在这里插入图片描述

例如：

import torch
Tensor=torch.ones([2,3,4,5])
# Data Type of every element: torch.float32
print("Data Type of every element:", Tensor.dtype)

Tensor所在设备

在这里插入图片描述

如图所示，我们可以看到每种类型的数据都有一个CPU和一个GPU版本，因此我们对张量进行处理的时候需要指定一个设备，它要么是CPU要么是GPU，这是数据被分配的位置，这决定了给定张量的张量计算位置。

Pytorch支持多种设备的使用，我们可以用torch.device来创建一个设备，并指定索引，例如：

device=torch.device('cuda:0')

输出结果为：device(type=‘cuda’,index=0)，可看到类型为’cuda’，即GPU，索引0表示为第一个GPU。

Tensor创建

直接创建张量

"""
data：数据，可以是list,numpy
dtype：数据类型，默认与data对应
device：张量所在的设备(cuda或cpu)
requires_grad：是否需要梯度
pin_memory：是否存于锁存内存
"""
torch.tensor(data,dtype=None,device=None,requires_grad=False,pin_memory=False)

pin_memory就是锁页内存，创建DataLoader时，设置pin_memory=True，则意味着生成的Tensor数据最开始是属于内存中的锁页内存，这样将内存的Tensor转义到GPU的显存就会更快一些。

import numpy as np
import torch
arr = np.ones((3, 3))
'''
[[1. 1. 1.]
 [1. 1. 1.]
 [1. 1. 1.]]
'''
print(arr)
# ndarray的数据类型： float64
print("ndarray的数据类型：", arr.dtype)
t= torch.tensor(arr)
'''
tensor([[1., 1., 1.],
        [1., 1., 1.],
        [1., 1., 1.]], dtype=torch.float64)
'''
print(t)

如需创建一个放在GPU的数据，则可做如下修改，运行结果同上。

import numpy as np
import torch
device= torch.device("cuda" if torch.cuda.is_available() else 'cpu')
arr = np.ones((3, 3))
print("ndarray的数据类型：", arr.dtype)
t = torch.tensor(arr, device=device)
print(t)

从numpy创建Tensor

torch.from_numpy(ndarray)

利用该方法创建的tensor与原ndarray共享内存，当修改其中一个数据，另外一个也会被更新。

import numpy as np
import torch
arr = np.array([[1, 2, 3], [4, 5, 6]])
t = torch.from_numpy(arr)
print(t)
# 修改tensor，array也会被修改
print("# -----------修改tensor--------------*")
t[0, 0] = -1
print("numpy array: ", arr)
print("tensor : ", t)

tensor([[1, 2, 3],
        [4, 5, 6]], dtype=torch.int32)
# -----------修改tensor--------------*
numpy array:  [[-1  2  3]
 [ 4  5  6]]
tensor :  tensor([[-1,  2,  3],
        [ 4,  5,  6]], dtype=torch.int32)

根据数值创建张量

  1. torch.zeros()：根据size创建全0张量
'''
size：张量的形状
out：输出的张量，如果指定了out，torch.zeros()返回的张量则会和out共享同一个内存地址
layout：内存中的布局方式，有strided，sparse_coo等。如果是稀疏矩阵，则可以设置为sparse_coo以减少内存占用
device：张量所在的设备(cuda或cpu)
requires_grad：是否需要梯度
'''
torch.zeros(*size, out=None, dtype=None, layout=torch.strided, device=None, requires_grad=False)

import torch
out_t = torch.tensor([1])
print(f"out_t初始值:{out_t}")
#指定out
t = torch.zeros((3, 3), out=out_t)
print(f"t:\n{t}")
print(f"out_t更新值:\n{out_t}")
# id是取内存地址，t和out_t是同一个内存地址
print(id(t), id(out_t), id(t) == id(out_t))

运行结果如下，由此可见，和out_t最终共享同一个内存地址。

out_t初始值:tensor([1])
t:
tensor([[0, 0, 0],
        [0, 0, 0],
        [0, 0, 0]])
out_t更新值:
tensor([[0, 0, 0],
        [0, 0, 0],
        [0, 0, 0]])
2083081770704 2083081770704 True
  1. torch.zeros_like：根据input形状创建全0张量
torch.zeros_like(input, dtype=None, layout=None, device=None, requires_grad=False, memory_format=torch.preserve_format)

同理还有全1张量的创建：torch.ones()，torch.ones_like()

  1. torch.full() & torch.full_like():创建自定义某一数值的张量。
'''
size：张量的形状，例如(3,3)
fill_value：张量中每一个元素的值。
'''

torch.full(size, fill_value, out=None, dtype=None, layout=torch.strided, device=None, requires_grad=False)

例如：

import torch
t = torch.full((4, 4), 10)
print(t)
'''
tensor([[10, 10, 10, 10],
        [10, 10, 10, 10],
        [10, 10, 10, 10],
        [10, 10, 10, 10]])
'''
  1. 创建等差的一维张量。

⭐注意区间为：[start,end)。

'''
start：数列起始值，默认为0
end：数列结束值，开区间，取不到结束值
step：数列公差，默认为1
'''
torch.arange(start=0, end, step=1, out=None, dtype=None, layout=torch.strided, device=None, requires_grad=False)

例如：

import torch
t = torch.arange(2, 10, 2)
print(t) # tensor([2, 4, 6, 8])
  1. torch.linspace()：创建均分的一维张量

⭐注意区间为：[start,end]。

'''
step：数列长度（元素个数）
'''
torch.linspace(start, end, steps=100, out=None, dtype=None, layout=torch.strided, device=None, requires_grad=False)

import torch
t = torch.linspace(2, 10, 3)
print(t) # tensor([ 2.,  6., 10.])
  1. torch.logspace()：创建对数均分的一维张量

⭐注意区间为：[start,end]。

'''
step：数列长度（元素个数）
base：对数函数的底，默认为 10
'''
torch.logspace(start, end, steps, base=10, out=None, dtype=None, layout=torch.strided, device=None, requires_grad=False)

import torch
t = torch.logspace(2, 4, 3)
print(t) # tensor([100.,  1000., 10000.])
  1. torch.eye()：创建单位对角矩阵（2维张量）

⭐默认输出方阵。

'''
n: 矩阵行数。因为是方阵，通常只设置n
m: 矩阵列数
'''
torch.eye(n, m=None, out=None, dtype=None, layout=torch.strided, device=None, requires_grad=False)

import torch
t = torch.eye(3)
h = torch.eye(3,4)
print(f"t:{t}")
print(f"h:{h}")

运行结果如下：

t:tensor([[1., 0., 0.],
        [0., 1., 0.],
        [0., 0., 1.]])
h:tensor([[1., 0., 0., 0.],
        [0., 1., 0., 0.],
        [0., 0., 1., 0.]])

根据概率创建张量

  1. torch.normal()：生成正态分布（高斯分布）

⭐返回一个张量，包含从给定参数means、std的离散正态分布中抽取的随机数。

'''
mean：均值
std：标准差
'''
torch.normal(mean, std, *, generator=None, out=None)

包含4种模式：

  • mean为标量，std为标量，此时需要设置size。

    import torch
t_normal = torch.normal(0., 1., size=(4,))
# t_normal:tensor([ 0.7098,  1.5432, -0.1568, -0.6350])
print(f"t_normal:{t_normal}")

  • mean为张量，std为标量。

    import torch
mean = torch.arange(1, 5, dtype=torch.float)
std = 1
t_normal = torch.normal(mean, std)
'''
mean:tensor([1., 2., 3., 4.])
std:1
'''
print("mean:{}\nstd:{}".format(mean, std))
#tensor([2.2450, 1.0230, 2.0299, 4.5855])
print(t_normal)

    这4个数采样分布的均值不同，但是方差都是 1。

  • mean为标量，std为张量。

    import torch
std = torch.arange(1, 5, dtype=torch.float)
mean = 2
t_normal = torch.normal(mean, std)
'''
mean:2
std:tensor([1., 2., 3., 4.])
'''
print("mean:{}\nstd:{}".format(mean, std))
# tensor([ 1.8482,  4.8143, -3.5074,  4.2010])
print(t_normal)

  • mean为张量，std为张量。

    import torch
mean = torch.arange(1, 5, dtype=torch.float)
std = torch.arange(1, 5, dtype=torch.float)
t_normal = torch.normal(mean, std)
'''
mean:tensor([1., 2., 3., 4.])
std:tensor([1., 2., 3., 4.])
'''
print("mean:{}\nstd:{}".format(mean, std))
# tensor([ 0.8195, -3.9112,  4.8498,  2.3934])
print(t_normal)

    其中0.8195是从正态分布N(1,1)中采样得到的，-3.9112是从正态分布N(2,2)中采样得到的，其他数字以此类推。

Tensor操作

形状重置

Tensor的shape可通过torch.reshape接口来改变。例如：

import torch
Tensor =torch.tensor([[[1, 2, 3, 4, 5],
                        [6, 7, 8, 9, 10]],
                      [[11, 12, 13, 14, 15],
                        [16, 17, 18, 19, 20]],
                      [[21, 22, 23, 24, 25],
                        [26, 27, 28, 29, 30]]])
print("the shape of Tensor:", Tensor.shape)
#利用reshape改变形状
reshape_Tensor = torch.reshape(Tensor, [2, 5, 3])
print("After reshape:\n", reshape_Tensor)

在这里插入图片描述

从输出结果看，将张量从[3, 2, 5]的形状reshape为[2, 5, 3]的形状时，张量内的数据不会发生改变，元素顺序也没有发生改变，只有数据形状发生了改变。

在指定新的shape时存在一些技巧：

  • -1 表示这个维度的值是从Tensor的元素总数和剩余维度自动推断出来的。因此，有且只有一个维度可以被设置为-1。
  • 0 表示该维度的元素数量与原值相同，因此shape中0的索引值必须小于Tensor的维度（索引值从 0 开始计，如第 1 维的索引值是 0，第二维的索引值是 1）。

例如：

# 直接指定目标 shape
origin:[3, 2, 5] reshape:[3, 10] actual: [3, 10]
# 转换为 1 维，维度根据元素总数推断出来是 3*2*5=30
origin:[3, 2, 5] reshape:[-1] actual: [30]
# 转换为 2 维，固定一个维度 5，另一个维度根据元素总数推断出来是 30÷5=6
origin:[3, 2, 5] reshape:[-1, 5]      actual: [6, 5]
# reshape:[0, -1]中 0 的索引值为 0，按照规则
# 转换后第 0 维的元素数量与原始 Tensor 第 0 维的元素数量相同，为3
# 第 1 维的元素数量根据元素总值计算得出为 30÷3=10。
origin:[3, 2, 5] reshape:[0, -1]      actual: [3, 10]
# reshape:[3, 1, 0]中 0 的索引值为 2
# 但原 Tensor 只有 2 维，无法找到与第 3 维对应的元素数量，因此出错。
origin:[3, 2] reshape:[3, 1, 0]       error：

另外还可以通过如下方式改变shape。

  • torch.squeeze：可实现Tensor的降维操作，即把Tensor中尺寸为1的维度删除。
  • torch.unsqueeze：可实现Tensor的升维操作，即向Tensor中某个位置插入尺寸为1的维度。
  • torch.flatten，将Tensor的数据在指定的连续维度上展平。
  • torch.transpose，对Tensor的数据进行重排。

索引和切片

通过索引或切片方式可访问或修改Tensor。

访问Tensor

import torch
ndim_2_Tensor = torch.tensor([[0, 1, 2, 3],
                               [4, 5, 6, 7],
                               [8, 9, 10, 11]])
print("Origin Tensor:\n", ndim_2_Tensor.numpy())
#索引或切片的第一个值对应第 0 维，第二个值对应第 1 维，
#依次类推，如果某个维度上未指定索引，则默认为 :
#所以下面两种操作结果一样
print("First row:", ndim_2_Tensor[0].numpy())
print("First row:", ndim_2_Tensor[0, :].numpy())
print("First column:", ndim_2_Tensor[:, 0].numpy())
print("Last column:", ndim_2_Tensor[:, -1].numpy())
print("All element:\n", ndim_2_Tensor[:].numpy())
print("First row and second column:", ndim_2_Tensor[0, 1].numpy())

在这里插入图片描述

修改Tensor

与访问张量类似，可以在单个或多个轴上通过索引或切片操作来修改张量。

import torch
ndim_2_Tensor = torch.ones([2, 3])
ndim_2_Tensor = ndim_2_Tensor.to(torch.float32)
print('Origin Tensor:\n ', ndim_2_Tensor)
# 修改第1维为0
ndim_2_Tensor[0] = 0
print('change Tensor:\n ', ndim_2_Tensor)
# 修改第1维为2.1
ndim_2_Tensor[0:1] = 2.1
print('change Tensor:\n ', ndim_2_Tensor)
# 修改全部Tensor
ndim_2_Tensor[...] = 3
print('change Tensor:\n ', ndim_2_Tensor)

在这里插入图片描述

Tensor运算

张量支持包括基础数学运算、逻辑运算、矩阵运算等100余种运算操作。

数学运算

x.abs()                       # 逐元素取绝对值
x.ceil()                      # 逐元素向上取整
x.floor()                     # 逐元素向下取整
x.round()                     # 逐元素四舍五入
x.exp()                       # 逐元素计算自然常数为底的指数
x.log()                       # 逐元素计算x的自然对数
x.reciprocal()                # 逐元素求倒数
x.square()                    # 逐元素计算平方
x.sqrt()                      # 逐元素计算平方根
x.sin()                       # 逐元素计算正弦
x.cos()                       # 逐元素计算余弦
x.add(y)                      # 逐元素加
x.subtract(y)                 # 逐元素减
x.multiply(y)                 # 逐元素乘（积）
x.divide(y)                   # 逐元素除
x.mod(y)                      # 逐元素除并取余
x.pow(y)                      # 逐元素幂
x.max()                       # 指定维度上元素最大值，默认为全部维度
x.min()                       # 指定维度上元素最小值，默认为全部维度
x.prod()                      # 指定维度上元素累乘，默认为全部维度
x.sum()                       # 指定维度上元素的和，默认为全部维度

逻辑运算

x.isfinite()                  # 判断Tensor中元素是否是有限的数字，即不包括inf与nan
x.equal_all(y)                # 判断两个Tensor的全部元素是否相等，并返回形状为[1]的布尔类Tensor
x.equal(y)                    # 判断两个Tensor的每个元素是否相等，并返回形状相同的布尔类Tensor
x.not_equal(y)                # 判断两个Tensor的每个元素是否不相等
x.less_than(y)                # 判断Tensor x的元素是否小于Tensor y的对应元素
x.less_equal(y)               # 判断Tensor x的元素是否小于或等于Tensor y的对应元素
x.greater_than(y)             # 判断Tensor x的元素是否大于Tensor y的对应元素
x.greater_equal(y)            # 判断Tensor x的元素是否大于或等于Tensor y的对应元素
x.allclose(y)                 # 判断两个Tensor的全部元素是否接近

矩阵运算

x.t()                         # 矩阵转置
x.transpose([1, 0])           # 交换第 0 维与第 1 维的顺序
x.norm('fro')                 # 矩阵的弗罗贝尼乌斯范数
x.dist(y, p=2)                # 矩阵（x-y）的2范数
x.matmul(y)                   # 矩阵乘法

Tensor广播机制

深度学习任务中，通常不可避免会遇到需要使用较小形状的Tensor与较大形状的Tensor执行计算的情况。此时，则需要将较小形状的Tensor扩展到与较大形状的Tensor一样的形状，以便于匹配计算，但是又不会对较小形状Tensor进行数据拷贝操作，从而提升算法实现的运算效率。这即是广播机制。

Tensor广播机制通常遵循如下规则：

  • 每个 Tensor 至少为一维 Tensor。

  • 从最后一个维度向前开始比较两个Tensor的形状，需要满足如下条件才能进行广播：

    • 两个Tensor的维度大小相等；或者其中一个Tensor的维度为1；或者其中一个Tensor的维度不存在。

例如：

  1. 两个Tensor的形状一致，可以广播。

    import torch

x = torch.ones((2, 3, 4))
y = torch.ones((2, 3, 4))
z = x + y
print(z)
# tensor([[[2., 2., 2., 2.],
         [2., 2., 2., 2.],
         [2., 2., 2., 2.]],

         [[2., 2., 2., 2.],
         [2., 2., 2., 2.],
         [2., 2., 2., 2.]]])
print(z.shape)
# torch.Size([2, 3, 4])

  2. 从最后一个维度向前依次比较：第一次y的维度大小为1，第二次x的维度大小为1，第三次x和y的维度大小相等，第四次y的维度不存在，所以x和y可以广播。

    import torch

x = torch.ones((2, 3, 1, 5))
y = torch.ones((3, 4, 1))

z = x + y
print(z.shape)
# torch.Size([2, 3, 4, 5])

  3. 从最后一个维度向前依次比较：第一次比较：4不等于6，不可广播。

    x = torch.ones((2, 3, 4))
y = torch.ones((2, 3, 6))
# z = x + y
# ValueError: (InvalidArgument) Broadcast dimension mismatch.

两个Tensor进行广播后的结果Tensor的形状计算规则如下：

  • 如果两个 Tensor 的形状的长度不一致，会在较小长度的形状矩阵前部添加 1，直到两个 Tensor 的形状长度相等。
  • 保证两个 Tensor 形状相等之后，每个维度上的结果维度就是当前维度上的较大值。

例如，y的形状长度为2，小于x的形状长度3，因此会在 y 的形状前部添加 1，结果就是 y 的形状变为[1, 3, 1]。广播之后z的形状为[2,3,4]，且z的每一维度上的尺寸，将取x和y对应维度上尺寸的较大值，如第0维x的尺寸为2，y的尺寸为1，则z的第0维尺寸为2。

import torch

x = torch.ones((2, 1, 4))
y = torch.ones((3, 1))

z = x + y
print(z.shape)
# torch.Size([2, 3, 4])

广播机制运行过程如下图。

在这里插入图片描述

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/548452.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

CloudCompare二次开发之如何通过PCL进行点云曲面重建？

CloudCompare二次开发之如何通过PCL进行点云曲面重建？

文章目录 0.引言1.CloudCompare界面设计重建(reconstruct)按钮2.使用贪婪三角化进行曲面重建（Surface_Rec） 0.引言 因笔者课题涉及点云处理，需要通过PCL进行点云数据一系列处理分析，查阅现有网络资料，对常用PCL点云曲面…
阅读更多...
SD webui 手记

SD webui 手记

源代码地址： https://github.com/AUTOMATIC1111/stable-diffusion-webui git拉取代码后，windows下支持根目录直接运行 webui-user.bat，前提本地需要先安装python环境，略过，我们直接跑源码玩 安装依赖 pip install …
阅读更多...
Linux 指令（二）+完整思维导图+实图例子+深入细节+通俗易懂建议收藏

Linux 指令（二）+完整思维导图+实图例子+深入细节+通俗易懂建议收藏

绪论 对于指令的学习，是一个漫长的过程，因为一般在后台服务器上为了减少刷新图形化界面消耗资源都是呈现出命令行的形式，对此我们必选要掌握好Linux的指令。今天我们接着上一章的指令来继续学习更多的指令。 话不多说安全带系好，发…
阅读更多...
字节给我狠狠上了一课：危机来的时候你连准备时间都没有！

字节给我狠狠上了一课：危机来的时候你连准备时间都没有！

各大互联网公司的接连裁员，政策限制的行业接连消失，让今年的求职雪上加霜，想躺平却没有资本，还有人说软件测试岗位饱和了，对此很多求职者深信不疑，因为投出去的简历回复的越来越少了。甚至还有不少大厂直接…
阅读更多...
【Linux】基本指令，拥抱Linux的第一步

【Linux】基本指令，拥抱Linux的第一步

[Linux]常见指令 Linux基本指令指令的本质ls指令pwd指令cd指令touch指令mkdir指令(重要)rmdir&&rm指令(重要)man指令（重要）cp指令（重要）mv指令（重要）重定向cat指令more指令less指令（重要…
阅读更多...
【C++模板】——template

【C++模板】——template

C模板 模板的引入函数模板函数模板的实例化模板参数匹配原则 类模板类模板的定义格式类模板的实例化 🍀小结🍀 🎉博客主页：小智_x0___0x_ 🎉欢迎关注：👍点赞🙌收藏✍️留言 &#x1…
阅读更多...
Unity之OpenXR+XR Interaction Toolkit如何自定义VR按键

Unity之OpenXR+XR Interaction Toolkit如何自定义VR按键

一.前言 上一篇文章我们介绍了Unity的新版本InputSyste如何使用，这一篇文章，我们主要说一下，在新版基于OpenXR的VR项目中，如何自定义VR按钮的功能。 二.Samples介绍 我们使用XR Interaction Toolkit插件时，它的几个Samples是非常有用的。如下所示： 它们分别是: 1.Sta…
阅读更多...
MySQL 教程---菜鸟教程

MySQL 教程---菜鸟教程

文章目录 MySQL 教程登录 MySQL数据库操作数据类型创建数据表删除数据表插入数据查询数据 MySQL 教程 关系型数据库管理系统（RDBMS） RDBMS 术语： 数据库：数据库是一些关联表的集合。数据表：表是数据的矩阵。在一个数…
阅读更多...
python 中常见变量类型

python 中常见变量类型

数值 a 10 b 123 … 字符串 在python中 用单引号’‘和双引号""括起来的都是字符串,不使用引号括起来的不是字符串，字符串是使用最多的数据类型，用来表示一段文本信息。 比如： a ‘123’ b “123” 字符串之间可以用加法运算…
阅读更多...
dubbo处理自定义异常

dubbo处理自定义异常

dubbo处理自定义异常 背景 在实际项目中，我们不可避免地需要使用自定义的异常，一般这个异常会继承RuntimeException，然后我们通过RestControllerAdvice注解，拦截业务异常类，做一些处理，但是在使用dubbo构…
阅读更多...
六级备考28天｜CET-6｜听力第三讲｜篇章的做题方法与练习法｜2022年6月考题9-11题｜16:15-17:15

六级备考28天｜CET-6｜听力第三讲｜篇章的做题方法与练习法｜2022年6月考题9-11题｜16:15-17:15

目录 1. 笔记 2. 听力原文复现 (9)问题9 (10)问题10 (11)问题11 08:00开始播放 两/三个选项大面积同时出现了听力中一句话，一般排除这两/三个选项 1. 笔记 2. 听力原文复现 (9)问题9 -What have researchers done for the first time in history? The re…
阅读更多...
c++ boost库学习-01-lexical_cast

c++ boost库学习-01-lexical_cast

一、C/C数值转换函数 C/C语言提供了几个标准库函数，可以将字符串、整型浮点型等相互转换。 atof()：将字符串转换为双精度浮点型值。 atoi()：将字符串转换为整型值。 atol()：将字符串转换为长整型值。 itoa()：将字符串…
阅读更多...
redis的几种集群方式

redis的几种集群方式

https://www.zhihu.com/people/pan-zhi-74-31 Redis集群介绍Redis集群一般有四种方式，分别为：主从复制、哨兵模式、Cluster以及各大厂的集群方案。在3.0版本之前只支持单实例模式，3.0之后支持了集群方式。在3.0之前各大厂为了解决单实例Redis…
阅读更多...
为Eclipse安装lombok插件

为Eclipse安装lombok插件

因为原生的Eclipse没有lombok插件，所以即使项目引入了lombok依赖也无法使用Data等常用标签。下面介绍一下如何手动为Eclipse添加lombok插件，具体操作步骤如下： （1）打开Download地址，点击页面中间的超链接下…
阅读更多...
k8s集群内带GPU工作节点配置显卡驱动

k8s集群内带GPU工作节点配置显卡驱动

k8s集群内带GPU工作节点配置显卡驱动 系统为Centos7 一、下载、安装显卡驱动 查看显卡型号 [rootVM-3-9-centos user]# lspci | grep -i nvidia 00:08.0 3D controller: NVIDIA Corporation TU104GL [Tesla T4] (rev a1)1.1、官网下载驱动程序 https://www.nvidia.cn/Downlo…
阅读更多...
数据分析13——Pandas数据导出/日期数据处理/样本采样

数据分析13——Pandas数据导出/日期数据处理/样本采样

Pandas数据导出 1、导出Excel： 举例： 代码：df.to_excel(‘./data/text_01.xlsx’, sheet_name‘订单明细’, indexFalse)解释：将df数据导入到相对路径为’./data/text_01.xlsx’的文件中，其中数据表名称为’订单明细…
阅读更多...
【算法】单源最短路径算法——Dijkstra算法

【算法】单源最短路径算法——Dijkstra算法

文章目录 一、简介与使用场景二、算法思想三、朴素版Dijkstra四、堆优化版Dijkstra五、总结 一、简介与使用场景 迪杰斯特拉算法(Dijkstra)是由荷兰计算机科学家狄克斯特拉于1959 年提出的，因此又叫狄克斯特拉算法。这是从一个顶点到其余各顶点的最短路径算法&#…
阅读更多...
STM32 使用SYN6288语音模块

STM32 使用SYN6288语音模块

文章目录 前言一、SYN6288介绍二、SYN6288原理讲解三.数据的异或校验四.代码编写1.串口的初始化2.SYN6288代码编写3.main函数逻辑 总结 前言 本篇文章带大家学习一下SYN6288语音模块，这个模块可以用于车载设备，语音电子书等众多产品当中，而且…
阅读更多...
Android 创建线程源码分析 JavaThreadNativeThread

Android 创建线程源码分析 JavaThreadNativeThread

前言 本文分析在Android中创建线程时候的源码分析，即JavaThread和NativeThread。 java/lang/Thread.java art/runtime/native/java_lang_Thread.cc art/runtime/thread.cc 两种Java Thread 有两种可以运行Java代码的线程。有两种情况： 通过new Thread创建的java线程在Nati…
阅读更多...
若依分离版——IDEA开发SpringBoot的webservice接口

若依分离版——IDEA开发SpringBoot的webservice接口

一.webservice介绍 WebService是帮助多个应用程序与平台和编程语言之间以独立的方式互相通信的标准化技术。它是利用标准 XML messaging(主要 SOAP) 技术，可以访问网络上的其他计算机的记述多种操作的软件接口。此接口主要由 WSDL (WebService Description Language…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023