回归预测 | MATLAB实现贝叶斯优化门控循环单元(BO-GRU)多输入单输出
目录
- 回归预测 | MATLAB实现贝叶斯优化门控循环单元(BO-GRU)多输入单输出
- 基本介绍
- 背景回顾
- 模型介绍
- 程序设计
- 学习总结
- 参考资料
- 致谢
基本介绍
本次运行测试环境MATLAB2020b;
本次预测基本任务是回归,多变量输入,单变量输出;
- 主要研究问题不限于交通预测、负荷预测、气象预测、经济预测等。Bayes-GRU多变量输入单变量输出,贝叶斯优化门控循环单元。
- 针对非线性预测模型出现参数过多及易陷入局部最优等问题,提出了一种深度学习中的门控制循环单元模型,并结合贝叶斯优化算法对门控制循环单元的超参数进行优化,为检验模型的可行性,以实测数据为基础,结果表明: 该模型的泛化能力强、运行效率高,能有效预测。
背景回顾
- 单一模型具有精度、鲁棒性和外延性较差的缺点,不同模型优化组合虽然在拟合和预测精度方面有较大提高,但是由于机器学习存在参数过多、收敛速度慢、极易陷入局部最优等问题,不能有效地处理高度
非线性问题。深度学习是由更多的非线性映射隐含层组成的一种神经网络,能较好地挖掘数据之间的非线性。 - 本文将具有全局优化能力的贝叶斯算法与门控制循环单元引入到预测分析中,可以解决监控模型收敛速度慢和过拟合的问题,并可提高模型的精度和稳定性,最终使预测更加准确。
模型介绍
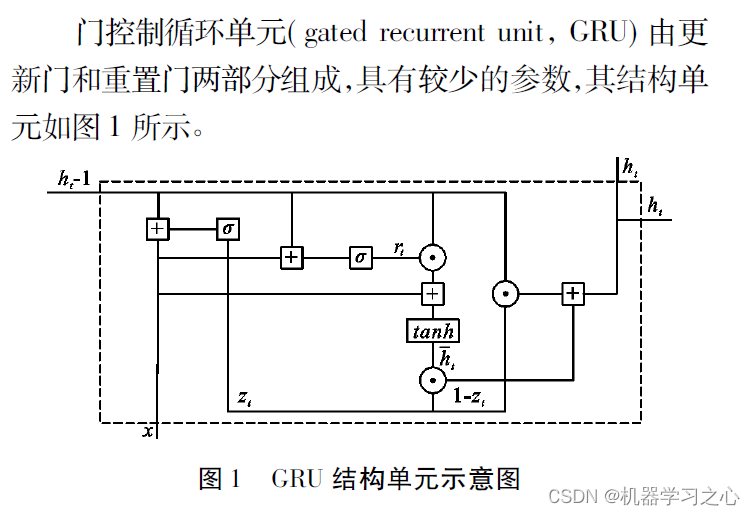
-
为提高模型预测精度,需要确定超参数最优组合。而贝叶斯优化( Bayesian optimization,BO) 是一种全局优化算法,能够有效地对GRU 模型中的参数进行寻优处理,从而实现具有非线性的监测数据预测。
-
本文基于贝叶斯算法对GRU模型的网络层数,单元数,学习率,正则化率共4 个超参数进行优化。概率代理模型选用树状结构Parzen 估计方法,采集函数为基于提升策略。自变量x 为不同超参数组合,优化目标函数为均方误差。
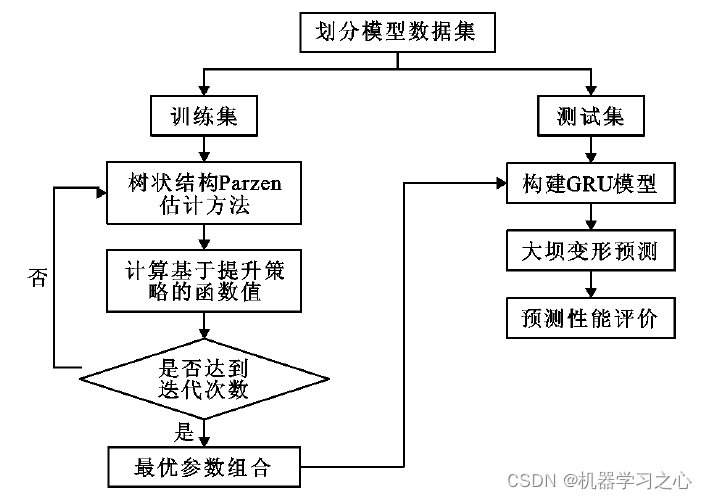
程序设计
%% 变量初始化
opt.learningMethod = 'GRU';
%% 参数定义
%最大迭代次数
opt.maxEpochs = 10;
%批处理大小
opt.miniBatchSize = 16;
%执行环境: 'cpu' 'gpu' 'auto'
opt.executionEnvironment = 'cpu';
%优化算法: 'sgdm' 'rmsprop' 'adam'
opt.LR = 'adam';
%训练进程: 'training-progress' 'none'
opt.trainingProgress = 'none';
%% 参数设定
opt.isUseDropoutLayer = true;
%权重丢失参数设定,防止过拟合
opt.DropoutValue = 0.5;
% 优化参数设定
opt.optimVars = [
optimizableVariable('NumOfLayer',[1 4],'Type','integer')
optimizableVariable('NumOfUnits',[50 200],'Type','integer')
optimizableVariable('InitialLearnRate',[1e-2 1],'Transform','log')
optimizableVariable('L2Regularization',[1e-10 1e-2],'Transform','log')];
opt.isUseOptimizer = true;
opt.MaxOptimizationTime = 14*60*60;
opt.MaxItrationNumber = 10;
opt.isDispOptimizationLog = true;
%参数保存设定
opt.isSaveOptimizedValue = false;
opt.isSaveBestOptimizedValue = true;
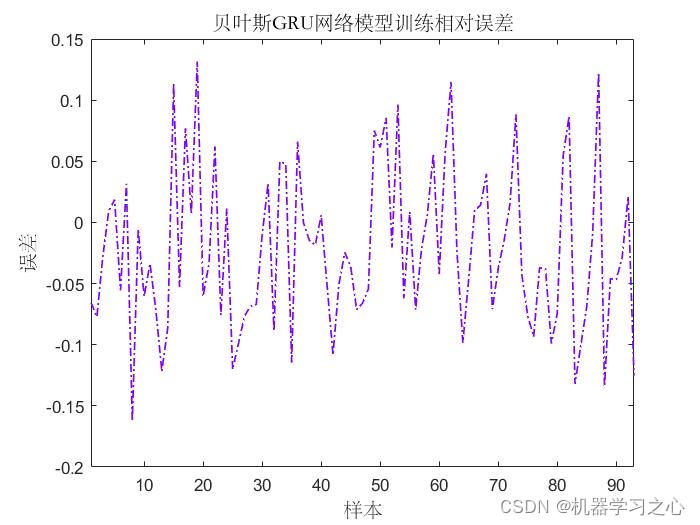
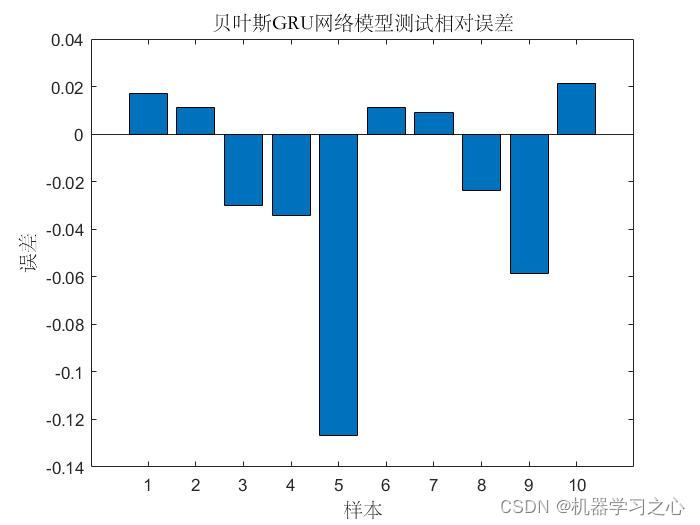
- 预测效果


学习总结
- 本文将贝叶斯优化算法和深度学习结合并引入到预测中,构建了基于Bayes-GRU模型,有效改善了模型易陷入局部最优的问题,从而提高了模型的精度和运行速度。
- 模型能够很好地处理具有非线性的数据,但是仍然存在梯度消失、记忆力不足的缺点,如何解决这些缺点,还需要做更深入地研究。
参考资料
[1] 黄梦婧,杨海浪,叶根苗.基于实时跟踪的大坝安全监控模型.
[2] 吴中如. 水工建筑物安全监控理论及其应用.
致谢
- 感谢大家订阅和支持!