机器学习吴恩达笔记第一篇——基于梯度下降的线性回归（零基础）

news2024/9/20 19:37:54

机器学习吴恩达笔记第一篇——基于梯度下降的线性回归（零基础）

一、线性回归——理论（单变量）

1、假设函数h(x)为：

$h(x)=\theta_0+\theta_1 X$

2、要拟合数据成一条直线，需要该直线上的预测的h(x)的值减去原来数据的y值：

$\mathop{minize}\limits_{\theta_0,\theta_1} (J(\theta))=\sum\limits_{i=1}^m(h_\theta(x^i)-y^i)^2/2m$

3、通过寻找一个合适的学习率与迭代次数来求得对应的 $\theta_0 , \theta_1$ ；

repeat until end{ #迭代到结束
$temp=\theta_j-\alpha \times(\frac{\partial J(\theta)}{\partial \theta_j})$
$\theta_j=temp$

}

注意： $\theta_j$ 需要同时更新；
4、计算出来 $\theta$ 值后，我们来判断 $J(\theta)$ 是否收敛：就是绘制在迭代过程中 $J(\theta)$ 的值；

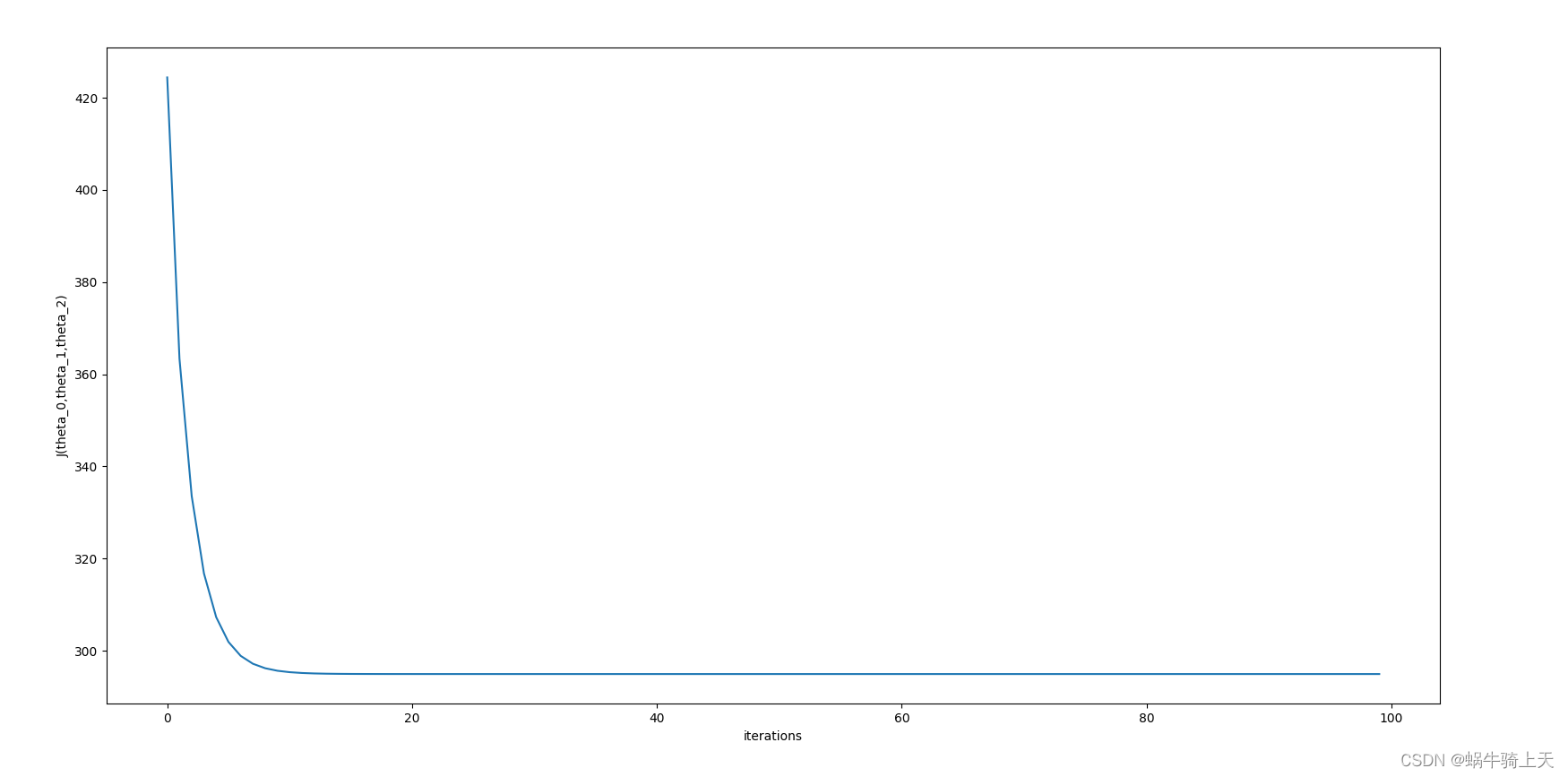
在这里插入图片描述

好了，理论部分就结束了，下一节就是介绍本节的基础知识；

二、基础知识（矩阵的乘法、梯度下降、学习率、迭代次数）

1.矩阵的乘法：

行乘列，列要与行相等；

import numpy as np
a=[1,2,3] #1*3
b=[4,5,6] #1*3
a=np.array(a)
b=np.array(b)
c=a.T*b 
#a.T:3*1
#  b:1*3
print(c)
#[ 4 10 18]

2.梯度下降

**repeat until end{ ** #迭代到结束

$\theta_j=\theta_j-\alpha \times(\frac{\partial J(\theta)}{\partial \theta_j})$

}

因为 $J(\theta)$ 是一个 $\sum\limits_{i=1}^m(h_\theta(x^i)-y^i)^2/2m$ 所以要求和；

使用迭代方法：

while i<iteration: #iteration=迭代次数；
    temp_0=sum((theta_0+theta_1*size+theta_2*num-price))        #theta_0
    temp_1=sum(size.T*(theta_0+theta_1*size+theta_2*num-price)) #theta_1
    i+=1

(theta_0+theta_1*size+theta_2*num-price)与size.T*(theta_0+theta_1*size+theta_2*num-price)都是求得偏导；

3.学习率

是决定收敛的重要条件：

收敛的时间长短：

$\alpha$ : 学习率；

repeat until end{ #迭代到结束

$\theta_j=\theta_j-\alpha \times(\frac{\partial J(\theta)}{\partial \theta_j})$

}
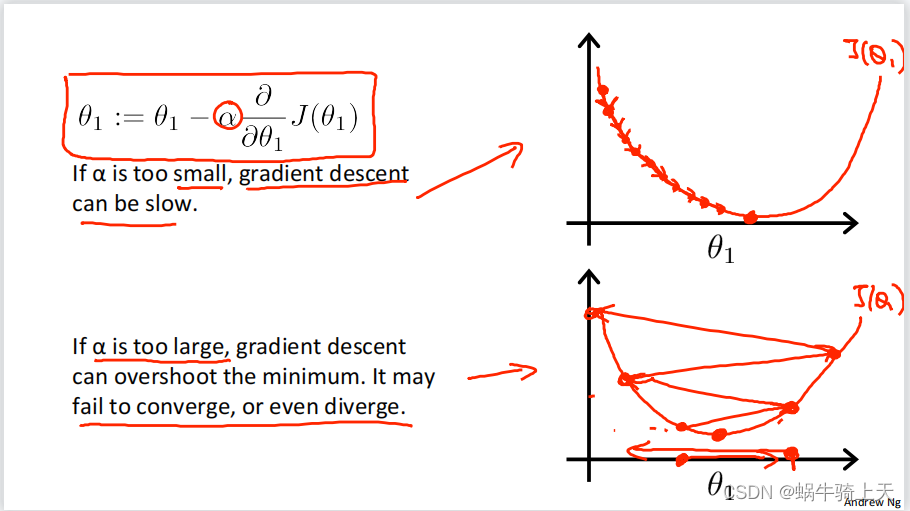
在这里插入图片描述

当 $\alpha$ 合适的时候会快速收敛；

是否收敛：

当 $\alpha$ 太大会不收敛，反复横跳；

4.迭代次数

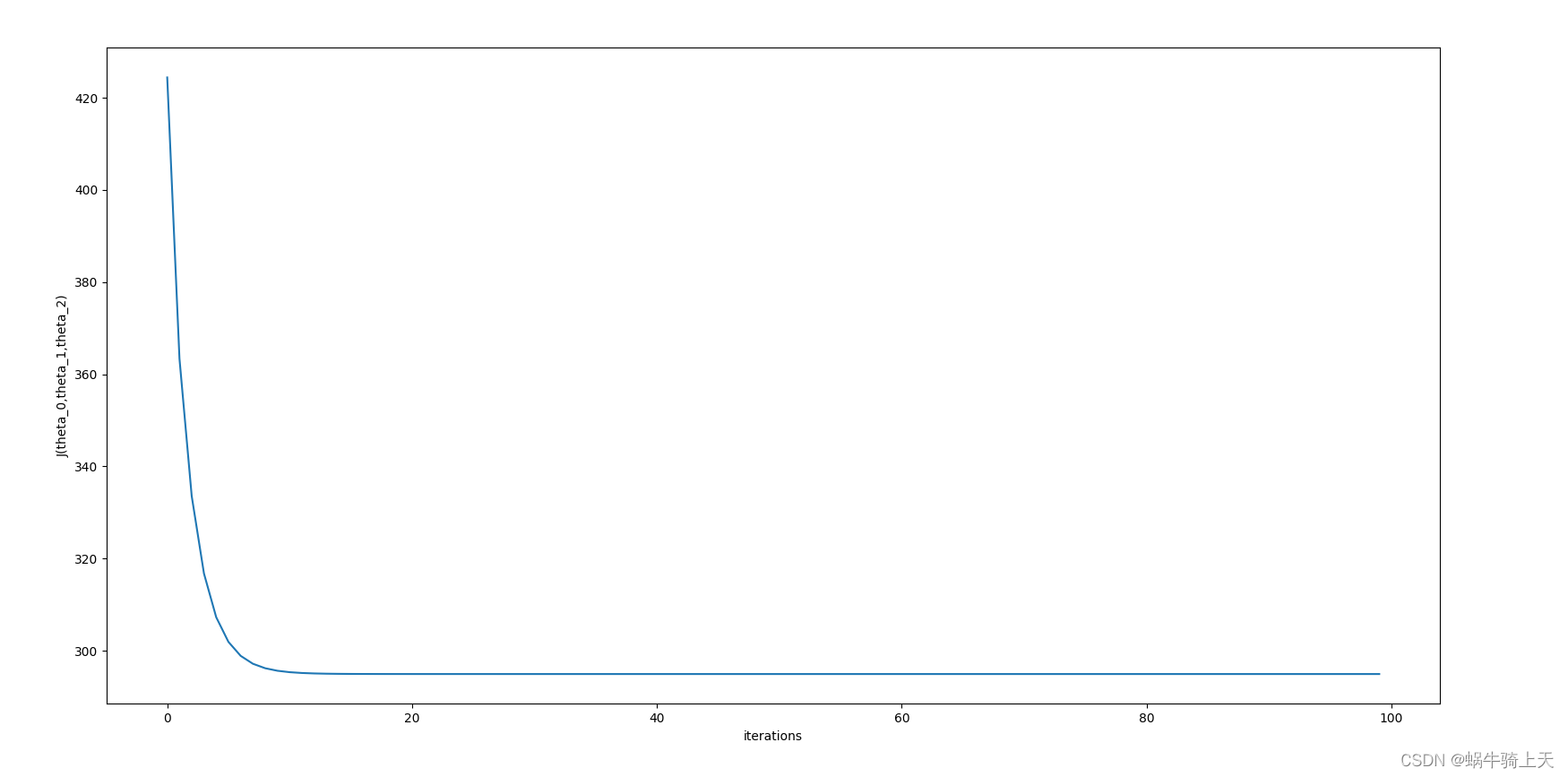
当迭代次数过少，就会不收敛；
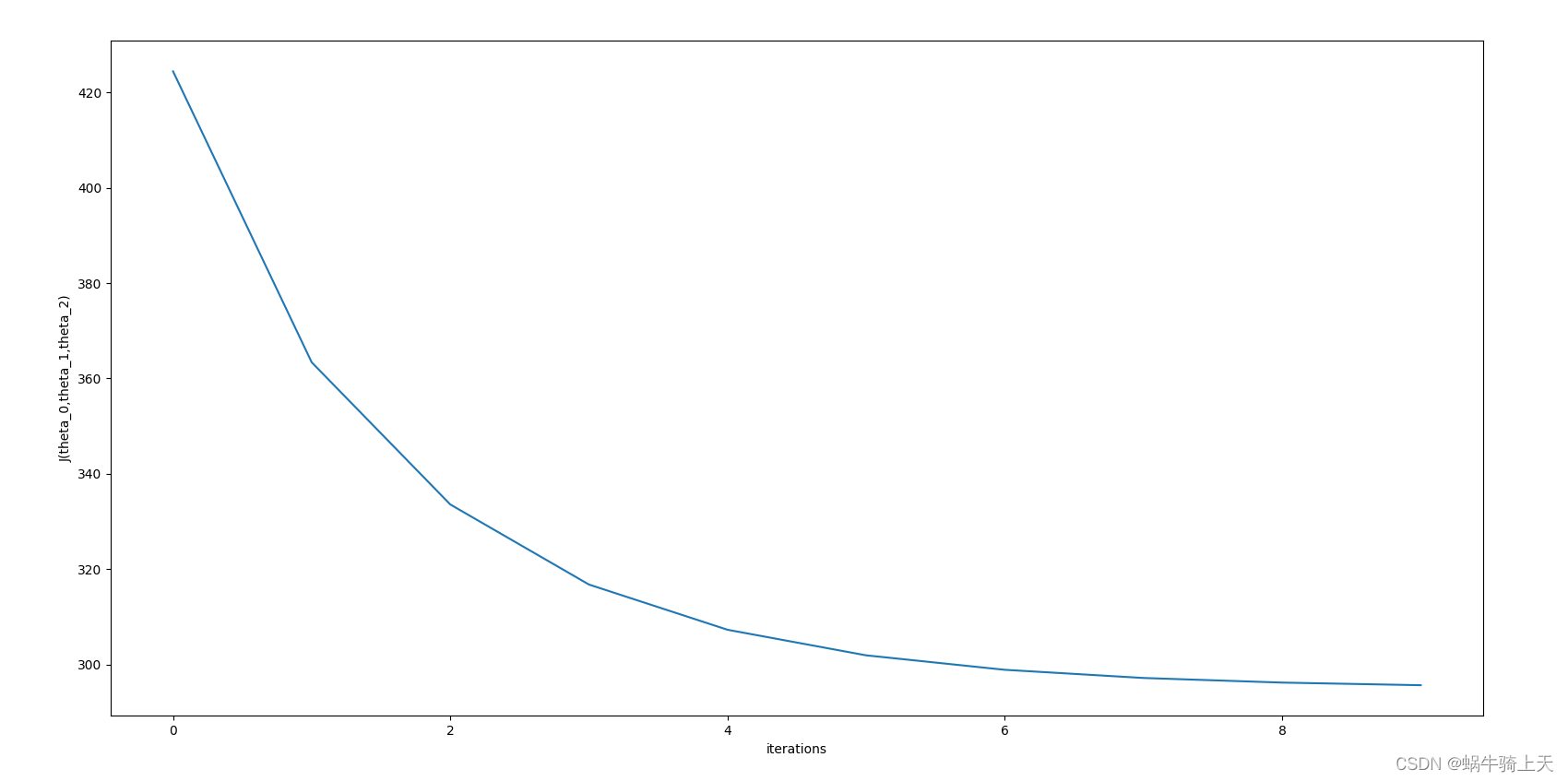
在这里插入图片描述

次数太少，没有收敛；

三、实现的代码

Python库

import matplotlib.pyplot as plt
import numpy as np
import math

读取文件

with open('ex1data1.txt','r') as f: # 文件划分；
    lines=f.readlines()
x=[]
y=[]
data=[]
for line in lines:
    data1=line.strip().split(',')
    x.append(float(data1[0]))
    y.append(float(data1[1]))
    data.append([float(data1[0]),float(data1[1])])
print(data)

画散点图

plt.scatter(x,y,c='red',marker='+',s=50,label='scatter') #散点图；
plt.xlabel('population')
plt.ylabel('predict')
plt.show()

在这里插入图片描述

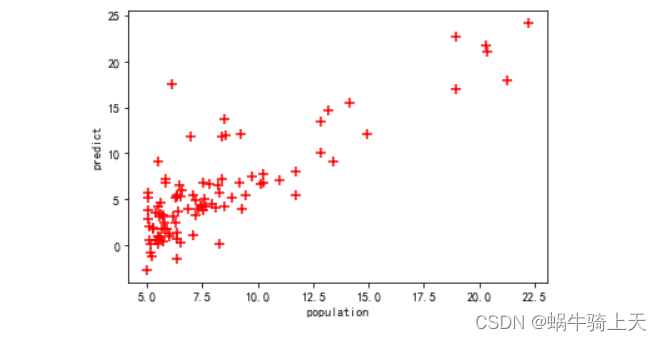
直线方程

def h(a,b,x): #函数方程；
    return a+b*x

拟合直线

m=len(x)#长度
rates=[0.012]#,0.003,0.01,0.03,0.1,0.3,1,3] #学习率；
iterations=[10000]#,30,100,300,1000]  #迭代次数；
s=[]
#"""
for rate in rates: #学习率；
    for iteration in iterations: # 迭代次数；
        i=0
        theta_0=0
        theta_1=0
        # 从0开始；
        J=[]
        flag=0
        while i<iteration:
            total=0
            temp_0=0
            temp_1=0
            for j,k in data:
                temp_0+=(theta_0+theta_1*j-k)  #J(theta_0)的偏导部分;
                temp_1+=(theta_0+theta_1*j-k)*j #J(theta_1)的偏导部分；
            #采集J(theta);
            #更新theta_0与theta_1;
            theta_0=theta_0-(temp_0*rate/m)
            theta_1=theta_1-(temp_1*rate/m)
            i+=1
            for j,k in data:
                total+=math.pow((theta_0+theta_1*j-k),2)
            J.append(total/(2*m))
        theta=range(len(J)) #长度；
        print('最后一的斜率*学习率是:{}'.format(temp_0)) #最后一个的值
        print('最后一的值是:{} {}'.format(theta_0,theta_1))
        x=np.linspace(4,24,200)
        y=h(theta_0,theta_1,x)
        plt.plot(x,y,label='linear regression')
        plt.xlabel('theta')
        plt.ylabel('J(theta)')
        plt.legend()
plt.show()

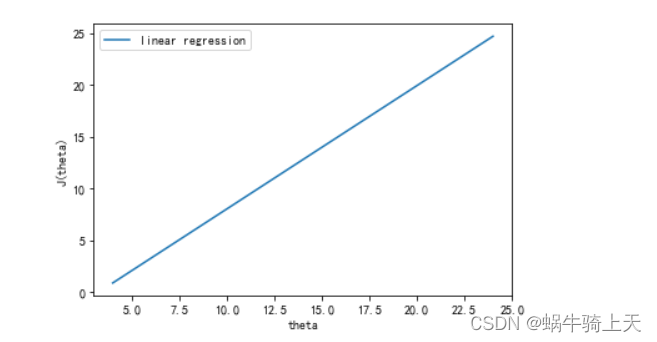
在这里插入图片描述

合并起来的效果是：

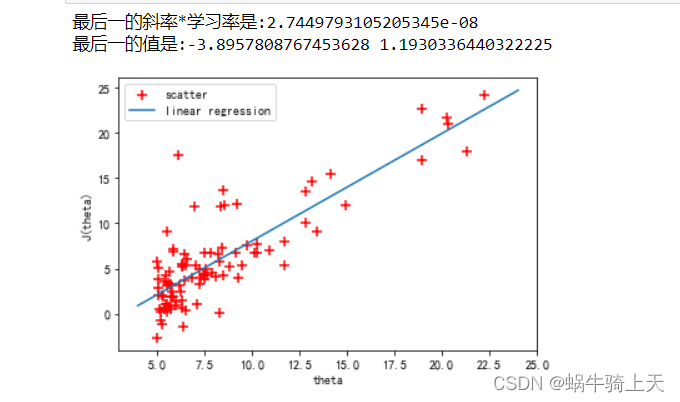
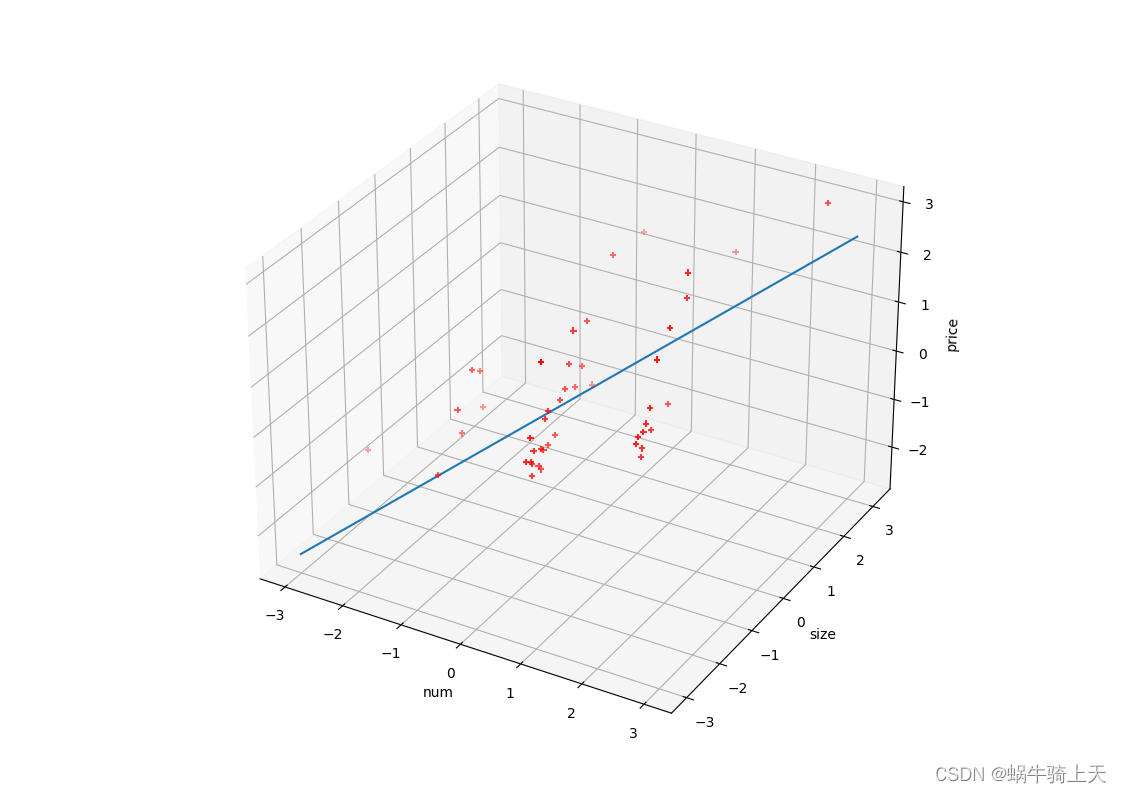
多元线性回归

多元线性回归只需要将方程改为:

$\times \theta_0+c \times \theta_1$

从而按上面的步骤来一步一步的做；

# -*- coding: utf-8 -*-
"""
Created on Fri May 12 14:27:25 2023

@author: windows
"""
import matplotlib.pyplot as plt
import numpy as np
def h(a,b,c,x,y):
    return a+b*x+c*y
def normoalize_feature(data): #归一化；
    data1=[]
    for data2 in data:
     data1.append((data2-data2.mean())/data2.std())
    return data1
def get_data(data):
    with open(data,'r') as f:
        lines=f.readlines()
    size,num,price=[],[],[] #房子的大小，卧室的数量，房子的价格；
    for line in lines:
        data1=(line.strip().split(','))
        size.append(float(data1[0]))     #缩小特征值；km^2
        num.append(float(data1[1]))
        price.append(float(data1[2]))  
    size,num,price=np.array(size),np.array(num),np.array(price)
    h=[size,num,price]
    return h
size,num,price=normoalize_feature(get_data('ex1data2.txt'))
print(size,num,price)
theta_0,theta_1,theta_2=0,0,0
# 3D
fig = plt.figure()
ax = fig.add_subplot(projection='3d')
ax.scatter(num,size,price,marker='+',c='red',cmap='coolwarm')
ax.set_xlabel('num')
ax.set_ylabel('size')
ax.set_zlabel('price')

rate=0.012
iteration=100
i=0
J=[] #J(theta)的值；
total=0
m=len(size)
while i<iteration:
    #求theta;
    temp_0,temp_1,temp_2=0,0,0
    temp_0=sum((theta_0+theta_1*size+theta_2*num-price)) #theta_0
    temp_1=sum(size.T*(theta_0+theta_1*size+theta_2*num-price)) #theta_1;
    temp_2=sum(num.T*(theta_0+theta_1*size+theta_2*num-price))
    theta_0,theta_1,theta_2=theta_0-rate*temp_0,theta_1-rate*temp_1,theta_2-rate*temp_2
    total=(theta_0+theta_1*size+theta_2*num-price).T*(theta_0+theta_1*size+theta_2*num-price)
    J.append(sum(total)/2*m)
    i+=1 
print(theta_0,theta_1,theta_2)
plt.subplot(projection='3d')
x=np.linspace(-3,3,200)
y=np.linspace(-3,3,200)
z=h(theta_0,theta_1,theta_2,x,y)
plt.plot(x,y,z)
plt.show()