目录
- 一、逻辑回归基本模型
- 二、处理多维特征输入
- 三、加载数据集
- 四、多分类问题
一、逻辑回归基本模型
基本模型: y ^ = σ ( x ∗ ω + b ) \hat{y} = \sigma (x * \omega + b) y^=σ(x∗ω+b),其中 σ ( ) \sigma() σ() 表示 sigmod 函数 σ ( x ) = 1 1 + e − x \sigma(x) = \frac{1}{1 + e^{-x}} σ(x)=1+e−x1。
二分类问题损失函数:二分类交叉熵(Binary Cross Entropy,BCE) l o s s = − ( y l o g y ^ + ( 1 − y ) l o g ( 1 − y ^ ) ) loss = -(y\ log\hat{y} + (1-y)\ log(1-\hat{y})) loss=−(y logy^+(1−y) log(1−y^))
Mini-Batch 版本: l o s s = − 1 N ∑ n = 1 N y n l o g y n ^ + ( 1 − y n ) l o g ( 1 − y n ^ ) loss = -\frac{1}{N} \sum_{n=1}^N y_n\ log\hat{y_n} + (1-y_n)\ log(1-\hat{y_n}) loss=−N1n=1∑Nyn logyn^+(1−yn) log(1−yn^)
代码实现:
import torch
import torch.nn.functional as F
import numpy as np
import matplotlib.pyplot as plt
x_data = torch.Tensor([[1.0], [2.0], [3.0]])
y_data = torch.Tensor([[0], [0], [1]])
class LogisticRegressionModel(torch.nn.Module):
def __init__(self):
super(LogisticRegressionModel, self).__init__()
self.linear = torch.nn.Linear(1, 1)
def forward(self, x):
y_pred = F.sigmoid(self.linear(x))
return y_pred
model = LogisticRegressionModel()
criterion = torch.nn.BCELoss(reduction='sum')
optimizer = torch.optim.SGD(model.parameters(), lr=0.01)
for epoch in range(1000):
y_pred = model(x_data)
loss = criterion(y_pred, y_data)
print(epoch, loss.item())
optimizer.zero_grad()
loss.backward()
optimizer.step()
x = np.linspace(0, 10, 200)
x_t = torch.Tensor(x).view((200, 1)) # view作用相当于reshape
y_t = model(x_t)
y = y_t.data.numpy() # 获取矩阵
plt.plot(x, y)
plt.plot([0, 10], [0.5, 0.5], c='r')
plt.xlabel('Hours')
plt.ylabel('Probability of Pass')
plt.grid()
plt.show()
二、处理多维特征输入
数据:
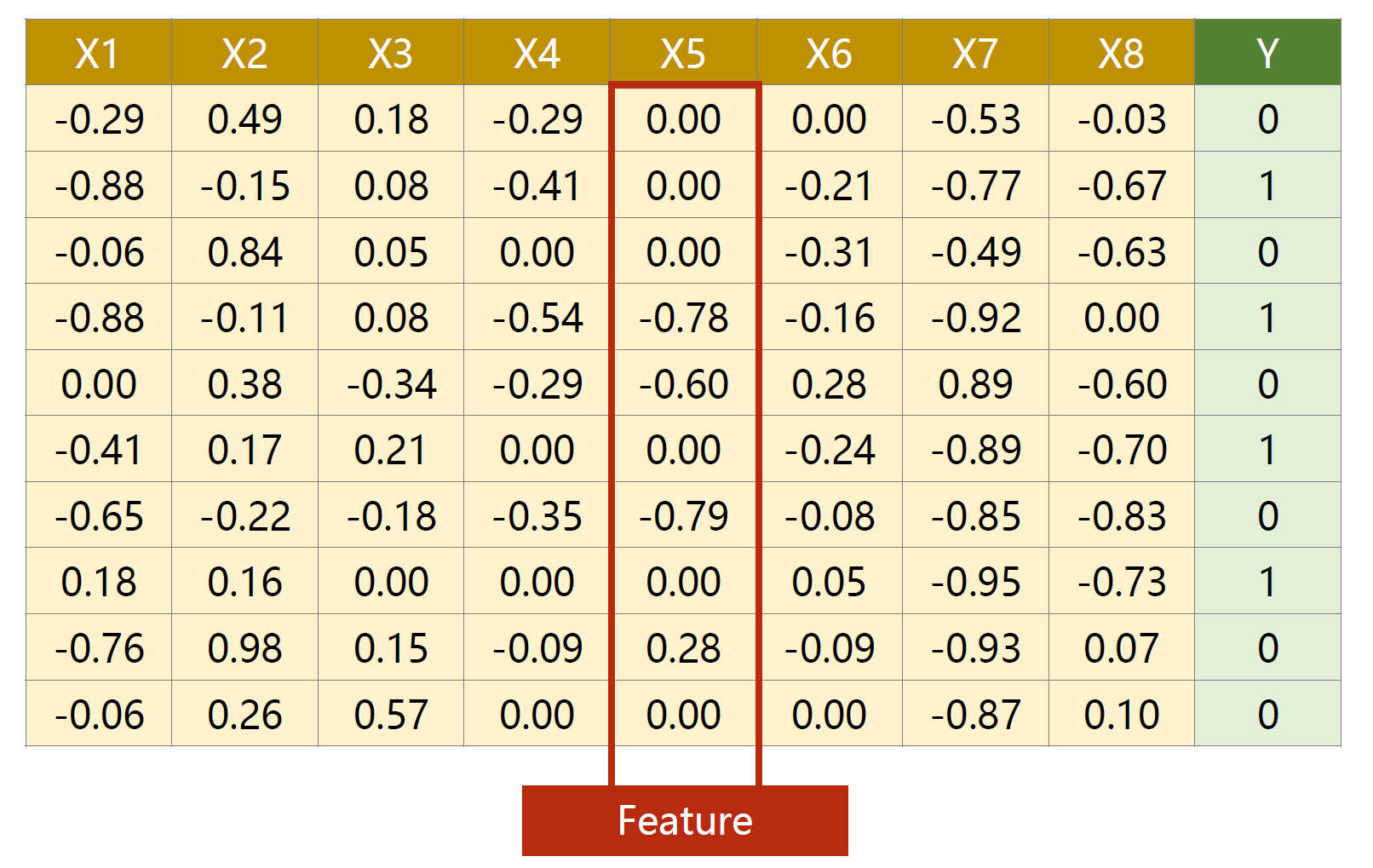
这是一个由 10 个 sample(每行称为一个 sample),每个 sample 有 8 个 feature 构成的数据集。
多维度数据输入的时候,模型会发生变化,即变成多维度逻辑回归模型:
y ^ ( i ) = σ ( x ( i ) ∗ ω + b ) ⇒ y ^ ( i ) = σ ( ∑ n = 1 8 x n ( i ) ∗ ω n + b ) = σ ( [ x 1 ( i ) ⋯ x 8 ( i ) ] [ ω 1 ⋮ ω 8 ] + b ) = σ ( z ( i ) ) \begin{aligned} \hat{y}^{(i)} = \sigma(x^{(i)} * \omega + b) \ \ \Rightarrow \ \ \hat{y}^{(i)} &= \sigma(\sum_{n=1}^8 x^{(i)}_n * \omega_n + b) \\ &= \sigma( \begin{bmatrix} x_1^{(i)} &\cdots &x_8^{(i)} \end{bmatrix} \begin{bmatrix} \omega_1 \\ \vdots \\ \omega_8 \end{bmatrix} +b )\\ &=\sigma(z^{(i)}) \end{aligned} y^(i)=σ(x(i)∗ω+b) ⇒ y^(i)=σ(n=1∑8xn(i)∗ωn+b)=σ([x1(i)⋯x8(i)] ω1⋮ω8 +b)=σ(z(i))
对于有 N 个 samples,即 Mini-Batch(N samples),其矩阵运算如下:
[ y ^ ( 1 ) ⋮ y ^ ( N ) ] = [ σ ( z ( 1 ) ) ⋮ σ ( z ( N ) ) ] = σ ( [ z ( 1 ) ⋮ z ( N ) ] ) \begin{bmatrix} \hat{y}^{(1)} \\ \vdots \\ \hat{y}^{(N)} \end{bmatrix}= \begin{bmatrix} \sigma(z^{(1)}) \\ \vdots \\ \sigma(z^{(N)}) \end{bmatrix} =\sigma( \begin{bmatrix} z^{(1)} \\ \vdots \\ z^{(N)} \end{bmatrix}) y^(1)⋮y^(N) = σ(z(1))⋮σ(z(N)) =σ( z(1)⋮z(N) )
其中:
z
(
1
)
=
[
x
1
(
1
)
⋯
x
8
(
1
)
]
[
ω
1
⋮
ω
8
]
+
b
⋮
z
(
N
)
=
[
x
1
(
N
)
⋯
x
8
(
N
)
]
[
ω
1
⋮
ω
8
]
+
b
\begin{aligned} z^{(1)} &= \begin{bmatrix} x_1^{(1)} &\cdots &x_8^{(1)} \end{bmatrix} \begin{bmatrix} \omega_1 \\ \vdots \\ \omega_8 \end{bmatrix} + b \\ &\vdots \\ z^{(N)} &= \begin{bmatrix} x_1^{(N)} &\cdots &x_8^{(N)} \end{bmatrix} \begin{bmatrix} \omega_1 \\ \vdots \\ \omega_8 \end{bmatrix} + b \\ \end{aligned}
z(1)z(N)=[x1(1)⋯x8(1)]
ω1⋮ω8
+b⋮=[x1(N)⋯x8(N)]
ω1⋮ω8
+b
可转换为矩阵运算(注意矩阵维度的变换):
[ z ( 1 ) ⋮ z ( N ) ] N × 1 = [ x 1 ( 1 ) ⋯ x 8 ( 1 ) ⋮ ⋱ ⋮ x 1 ( N ) ⋯ x 8 ( N ) ] N × 8 [ ω 1 ⋮ ω 8 ] 8 × 1 + [ b ⋮ b ] N × 1 \begin{bmatrix} z^{(1)} \\ \vdots \\ z^{(N)} \end{bmatrix}_{N \times 1} = \begin{bmatrix} x_1^{(1)} &\cdots &x_8^{(1)} \\ \vdots &\ddots &\vdots \\ x_1(N) &\cdots &x_8^{(N)} \end{bmatrix}_{N \times 8} \begin{bmatrix} \omega_1 \\ \vdots \\ \omega_8 \end{bmatrix}_{8 \times 1} + \begin{bmatrix} b\\ \vdots\\ b \end{bmatrix}_{N \times 1} z(1)⋮z(N) N×1= x1(1)⋮x1(N)⋯⋱⋯x8(1)⋮x8(N) N×8 ω1⋮ω8 8×1+ b⋮b N×1
矩阵变换,实质上是一种空间变换的函数,上述变换过程就将输入 feature=8 的空间映射到输出 feature=1 的空间。同样,也可以实现从 feature=8 映射到输出 feature=x 的空间,其中 x 可以自行设置。
上面过程都是线性变换的,需要在每一次映射之后引入一个非线性函数(比如 sigmod 函数),使得该神经网络可以去拟合一个非线性的变换。
这里的目标是将 feature=8 映射到 feature=1,但是由上面矩阵变换的性质,这里可以分步将 feature 从 8 降到 1,这样这个分类的神经网络模型就可以由很多层构成,这样我们模型的拟合能力就越强,如下图:

上图中 feature 降维的过程是 8 → 6 → 4 → 1。
代码实现:
import numpy as np
import torch
xy = np.loadtxt('./Data/diabetes.csv.gz', delimiter=',', dtype=np.float32) # 分隔符为',',读取数据格式一般为浮点数32位即可
x_data = torch.from_numpy(xy[:, :-1]) # 最后一列不取
y_data = torch.from_numpy(xy[:, [-1]]) # [-1]表示只取最后一列,并且形成矩阵
class Model(torch.nn.Module):
def __init__(self):
super(Model, self).__init__()
self.linear1 = torch.nn.Linear(8, 6) # 第一层feature从8到6
self.linear2 = torch.nn.Linear(6, 4) # 第二层feature从6到4
self.linear3 = torch.nn.Linear(4, 1) # 第二层feature从4到1
self.sigmoid = torch.nn.Sigmoid()
def forward(self, x):
x = self.sigmoid(self.linear1(x))
x = self.sigmoid(self.linear2(x))
x = self.sigmoid(self.linear3(x))
return x
model = Model()
criterion = torch.nn.BCELoss(reduction='sum')
optimizer = torch.optim.SGD(model.parameters(), lr=0.01)
for epoch in range(1000):
y_pred = model(x_data)
loss = criterion(y_pred, y_data)
print(epoch, loss.item())
optimizer.zero_grad()
loss.backward()
optimizer.step()
三、加载数据集
Pytorch 中有两个工具:
- Dataset:构建数据集,支持索引,在 Pytorch 中,它是一个抽象类,只能被继承,不能被实例化。
- DataLoader:从 Dataset 中拿出一个 Mini-Batch 这样一组数据用于训练,在 Pytorch 中,它是一个类,可以被实例化。
在上一节的代码中,每一次梯度下降将所有数据都进行了运算,会比较浪费时间。如果每次梯度下降仅使用一个点的梯度,这样带来的好处是可以克服求导时的鞍点,这样训练出的模型性能可能会更好,但是训练时优化的时间会非常长。所以折中便是用部分数据进行梯度下降,即一个 Mini-Batch。
几个概念需要了解:
- Epoch:One forward pass and one backword pass of all the training examples,即所有样本都进行过一次前馈、反馈传播训练就成为一次 Epoch。
- Batch-Size:The number of training examples in one forward backward pass,即一次训练所使用的样本数量,或者说是一次 Epoch 的样本数量。
- Iterations:Number of passes, each pass using batch-size number of examples,举一个例子,假设由 10000 个样本,Batch-Size = 1000, 那么 Iterations = 10000 / Batch-Size =10。
DataLoader 的工作流程:

import numpy as np
import torch
from torch.utils.data import Dataset, DataLoader
class DiabetesDataset(Dataset):
def __init__(self, filePath):
xy = np.loadtxt(filePath, delimiter=',', dtype=np.float32)
self.len = xy.shape[0] # 有多少个sample
self.x_data = torch.from_numpy(xy[:, :-1]) # 最后一列不要
self.y_data = torch.from_numpy(xy[:, [-1]]) # 仅取最后一列且形成矩阵
def __getitem__(self, item): # 根据索引返回数据
return self.x_data[item], self.y_data[item]
def __len__(self): # 返回数据中sample的个数
return self.len
dataset = DiabetesDataset('./Data/diabetes.csv.gz')
# print(len(dataset))
train_loader = DataLoader(dataset=dataset, batch_size=32, shuffle=True) # 读取数据进程数目设置为2,但是这里设置多线程会报错
class Model(torch.nn.Module):
def __init__(self):
super(Model, self).__init__()
self.linear1 = torch.nn.Linear(8, 6)
self.linear2 = torch.nn.Linear(6, 4)
self.linear3 = torch.nn.Linear(4, 1)
self.sigmoid = torch.nn.Sigmoid()
def forward(self, x):
x = self.sigmoid(self.linear1(x))
x = self.sigmoid(self.linear2(x))
x = self.sigmoid(self.linear3(x))
return x
model = Model()
criterion = torch.nn.BCELoss(reduction='sum')
optimizer = torch.optim.SGD(model.parameters(), lr=0.01)
for epoch in range(100): # 对所有数据100次
for i, (x, y) in enumerate(train_loader, 0):
# 这里x、y自动转换为了tensor
# 每一次取出一个batch-size=32,共759个samples,所以iterations=759/32=23
y_pred = model(x)
loss = criterion(y_pred, y)
print(epoch, i, loss.item())
optimizer.zero_grad()
loss.backward()
optimizer.step()
四、多分类问题
针对 MNIST 数据集,其中存在 10 中手写数字标签( 0 ∼ 10 0\sim10 0∼10),如下图所示:
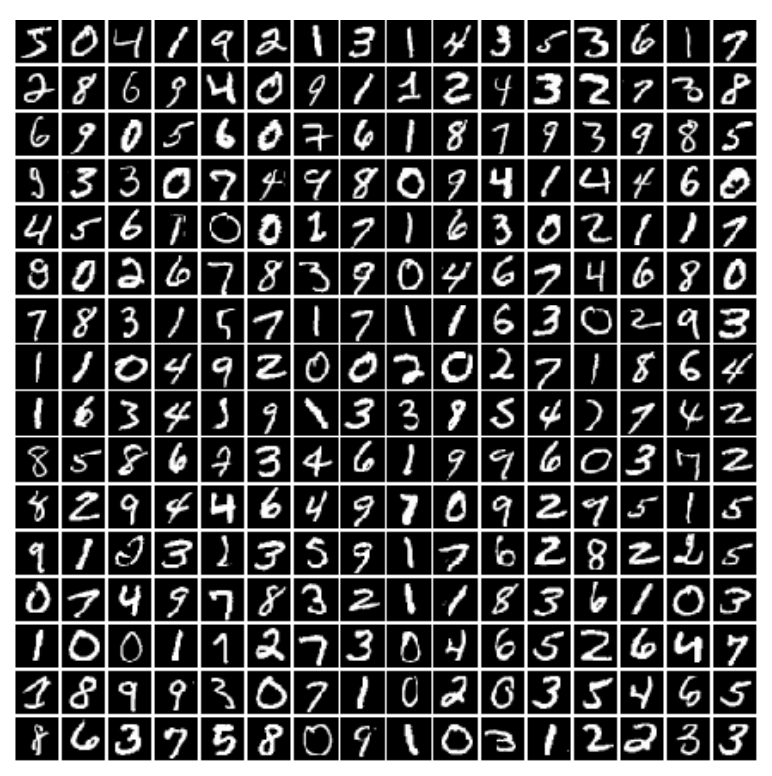
按照二分类问题的思路,在每一层结束的时候使用激活函数 sigmoid,那么最终输出的结果就会十个值,如下图所示:

并且 ∑ n = 1 10 y ^ n ≠ 1 \sum_{n=1}^{10} \hat{y}_n \ne 1 n=1∑10y^n=1这样并不能很好地预测出结果,为了使输出结果能够给相互抑制且呈现出一个分布状态,使用 Softmax 作为最后一层的激活函数,如下图所示:
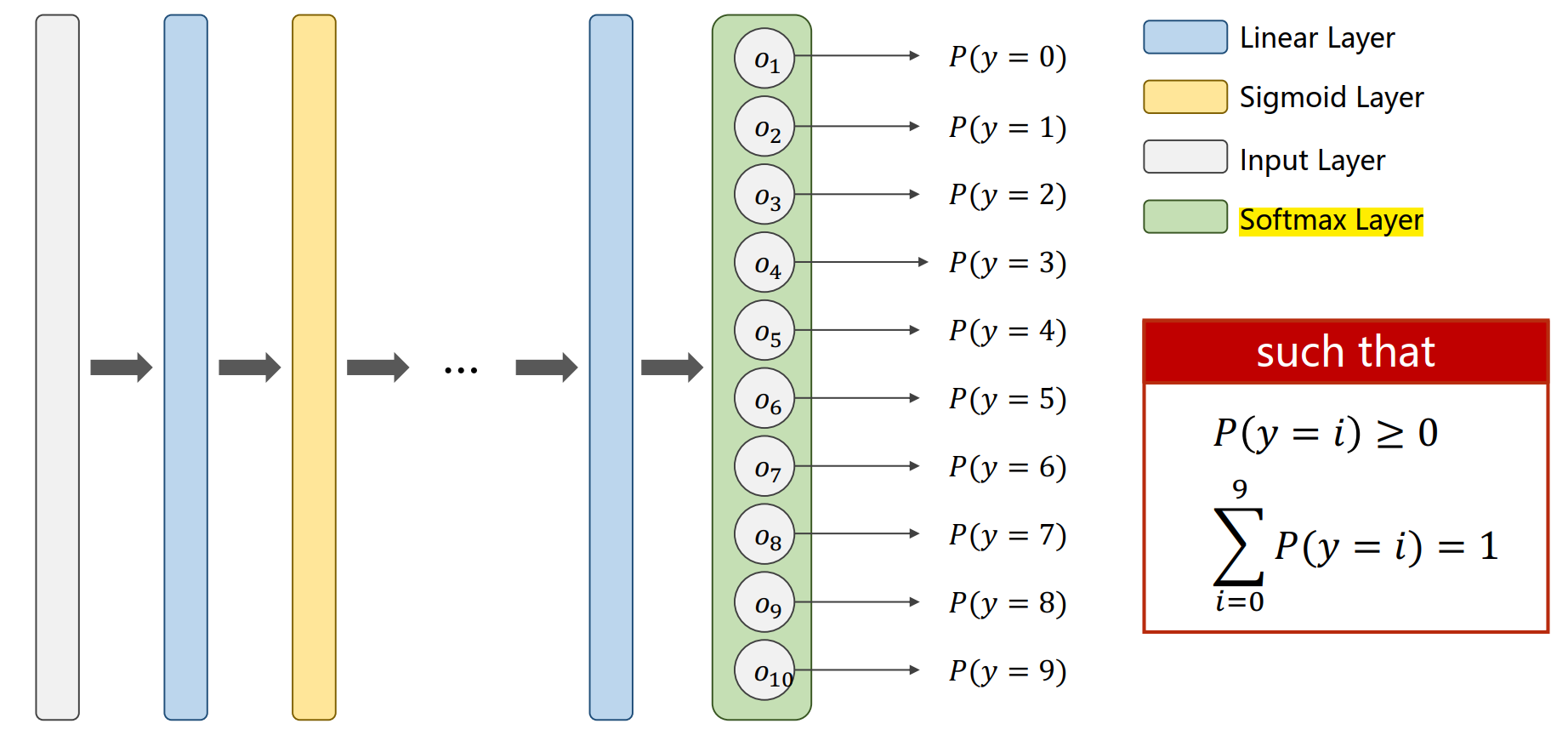
在 Softmax 层中的计算:假设最后一层的输出位 Z l ∈ R K Z^l \in R^K Zl∈RK,则有 P ( y = i ) = e Z i ∑ j = 0 K − 1 e Z j P(y=i) = \frac{e^{Z_i}}{\sum_{j=0}^{K-1} e^{Z_j}} P(y=i)=∑j=0K−1eZjeZi其中 i ∈ { 0 , ⋯ , K − 1 } i \in \{0, \cdots, K-1 \} i∈{0,⋯,K−1}。
将上式应用到 MNIST 数据集中,就会有 P ( y = i ) > 0 P(y=i) > 0 P(y=i)>0,并且 ∑ i = 1 10 P ( y = i ) = 1 \sum_{i=1}^{10} P(y=i)= 1 ∑i=110P(y=i)=1。
对于多分类问题的损失函数:交叉熵损失函数
- 如果使用 Numpy 来实现:
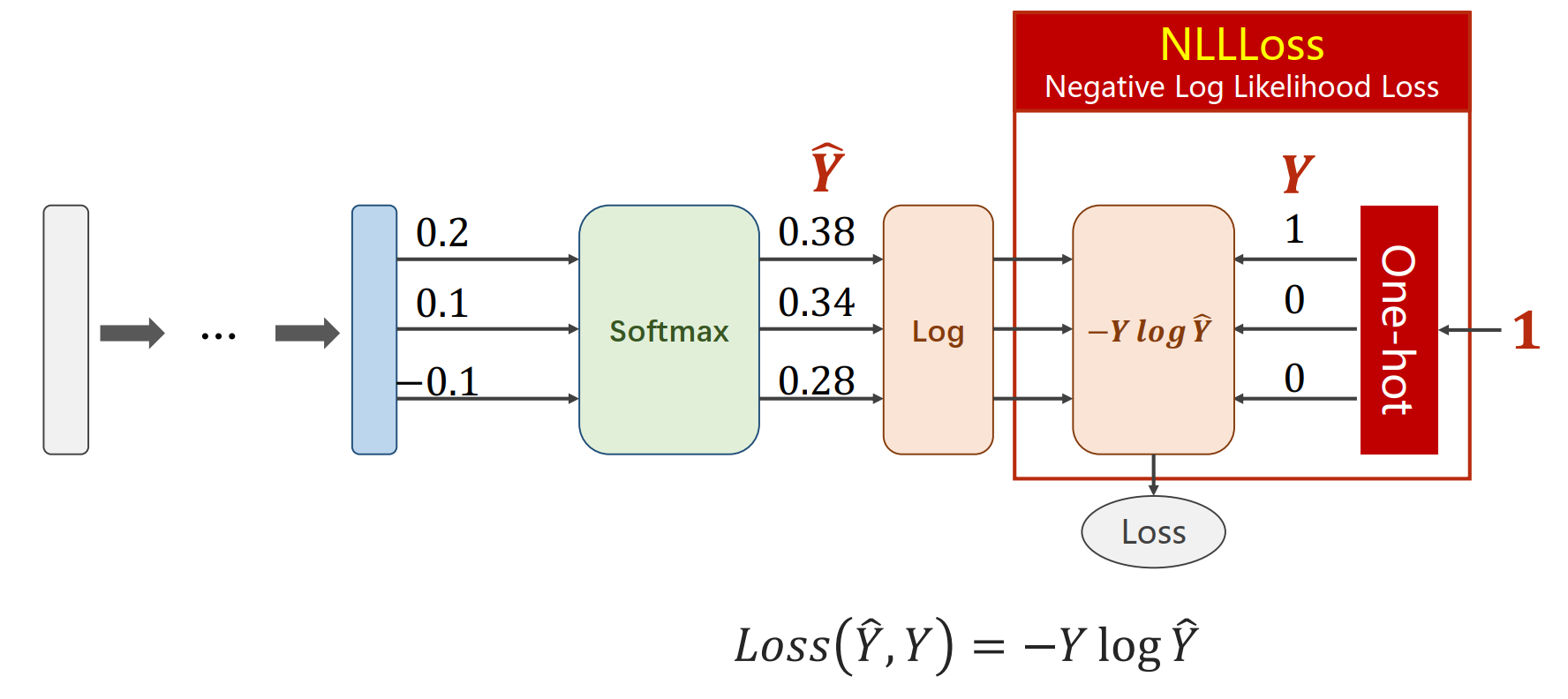
代码如下:
import numpy as np
y = np.array([1, 0, 0])
z = np.array([0.2, 0.1, -0.1])
y_pred = np.exp(z) / np.exp(z).sum()
loss = (-y * np.log(y_pred)).sum()
print(loss)
- 如果使用 Pytorch 来实现:
代码实现如下:
import torch
y = torch.LongTensor([0]) # y必须是一个 LongTensor
z = torch.Tensor([[0.2, 0.1, -0.1]]) # 最后一层不能使用激活函数
criterion = torch.nn.CrossEntropyLoss()
loss = criterion(z, y)
print(loss.item())
针对 MNIST 数据集的多分类识别:
最终精度只能达到 97%
import torch
from torchvision import transforms
from torchvision import datasets
from torch.utils.data import DataLoader
import torch.nn.functional as F
import torch.optim as optim
batch_size = 64
transform = transforms.Compose(
[transforms.ToTensor(), transforms.Normalize((0.1307,), (0.3081,))]) # 归一化并将图像从单通道转换为多通道,即28x28转换为1x28x28
train_dataset = datasets.MNIST(root='./Data/mnist/', train=True, download=True, transform=transform)
train_loader = DataLoader(train_dataset, shuffle=True, batch_size=batch_size)
test_dataset = datasets.MNIST(root='./Data/mnist', train=False, download=True, transform=transform)
test_loader = DataLoader(test_dataset, shuffle=False, batch_size=batch_size)
class Net(torch.nn.Module):
def __init__(self):
super(Net, self).__init__()
self.l1 = torch.nn.Linear(784, 512)
self.l2 = torch.nn.Linear(512, 256)
self.l3 = torch.nn.Linear(256, 128)
self.l4 = torch.nn.Linear(128, 64)
self.l5 = torch.nn.Linear(64, 10)
def forward(self, x):
x = x.view(-1, 784)
x = F.relu(self.l1(x))
x = F.relu(self.l2(x))
x = F.relu(self.l3(x))
x = F.relu(self.l4(x))
x = self.l5(x) # 最后一层不激活
return x
model = Net()
criterion = torch.nn.CrossEntropyLoss()
optimizer = optim.SGD(model.parameters(), lr=0.01, momentum=0.5) # 添加了动量
def train(epoch): # 将每一轮训练封装成一个函数
running_loss = 0.0
for batch_idx, data in enumerate(train_loader, 0):
inputs, target = data
optimizer.zero_grad()
outputs = model(inputs)
loss = criterion(outputs, target)
loss.backward()
optimizer.step()
running_loss += loss.item()
if batch_idx % 300 == 299:
print('[%d, %5d] loss: %.3f' % (epoch + 1, batch_idx + 1, running_loss / 300))
running_loss = 0.0
def test():
correct = 0 # 预测正确的数目
total = 0 # 总共的数目
with torch.no_grad(): # with范围内的代码不计算梯度
for data in test_loader:
images, labels = data
outputs = model(images)
_, predicted = torch.max(outputs.data, dim=1) # 返回(最大值, 最大值下标)
total += labels.size(0) # label是一个矩阵
correct += (predicted == labels).sum().item()
print('Accuracy on test set: %d %%' % (100 * correct / total))
if __name__ == '__main__':
for epoch in range(10):
train(epoch)
test()