3.程序调试与实践:数据存储与运算
3.1真值与机器数
真值: 数据在现实世界中的表示
机器数: 数据在计算机内部的二进制编码表示
温度:零下3.5度
习惯写法:-3.5 (数据的真值/数据的实际值)
3.1.1整数的编码
带符号整数:
char、short、int、long无符号整数:
unsigned char、unsigned short、unsigned int
-
示例代码1
#include<stdio.h> int main() { int ai = 100,bi = 2147483648,ci = -100; // 2^31== 2147483648 unsigned au = 100,bu = 2147483648,cu = -100; printf("ai=%d, bi=%d, ci=%d\n",ai,bi,ci); printf("au=%u, bu=%u, cu=%u\n",au,bu,cu); return 0; } -
示例代码1编译运行
./manu ai=100, bi=-2147483648, ci=-100 au=100, bu=2147483648, cu=4294967196问题:带符号整数
bi的输出结果值为何是负数?无符号整数
cu,赋值-个负的数据后,cu输出的结果为什么会是这个值?cu在计算机中实际存储的内容是什么?
-
反汇编查看示例1代码
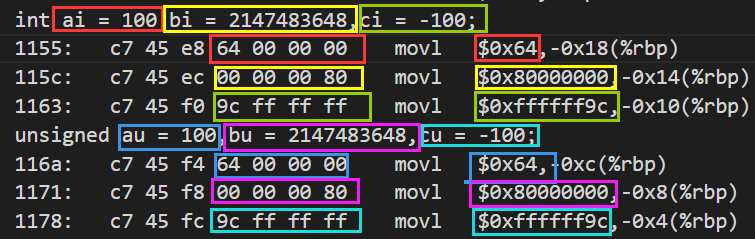
相同颜色为对应值
-
问题回答
bi编码成为0xffffff9c,符号位为1,为负数,所以输出为负数。cu编码成为0xffffff9c,对于无符号整数来说,换算成十进制就是4294967196带符号整数: 补码

无符号整数: 二进制编码

3.2数据的存储
-
示例代码
#include "stdio.h" void main() { char a = 100; short b = 100; int c = 100; int d = 0x12345678; printf("a=%0xH,b=%0xH,c=%0xH,d=%0xH\n", a, b, c, d); } -
调试
(gdb) i r rsp rbp rsp 0x7ffffffedde0 0x7ffffffedde0 rbp 0x7ffffffeddf0 0x7ffffffeddf0 ...//执行完 int d = 0x12345678; (gdb) x/16xb $rsp 0x7ffffffedde0: 0xe0 0xde 0xfe 0xff 0xff 0x64 0x64 0x00 0x7ffffffedde8: 0x64 0x00 0x00 0x00 0x78 0x56 0x34 0x12变量在栈帧中的存储,因为系统是小端模式。
大端方式:最高有效字节存放在低地址单元中,
最低有效字节存放在高地址单元中。小端方式:最高有效字节存放在高地址单元中,
最低有效字节存放在低地址单元中。
3.3数组的对齐
-
示例代码
#include "stdio.h" void main() { struct record { char a; int b; short c; char d; } R[2]; R[0].a = 1; R[0].b = 2; R[0].c = 3; R[0].d = 4; R[1].a = 5; R[1].b = 6; R[1].c = 7; R[1].d = 8; printf("数据存储时的边界对齐"); } -
调试
...//运行完R[1].d = 8; (gdb) x/32xb $rsp 0x7ffffffeddd0: 0x01 0x00 0x00 0x00 0x02 0x00 0x00 0x00 0x7ffffffeddd8: 0x03 0x00 0x04 0x08 0x05 0x00 0x00 0x00 0x7ffffffedde0: 0x06 0x00 0x00 0x00 0x07 0x00 0x08 0x00 0x7ffffffedde8: 0x00 0x8c 0x05 0x6b 0xb3 0xa8 0xe2 0x8c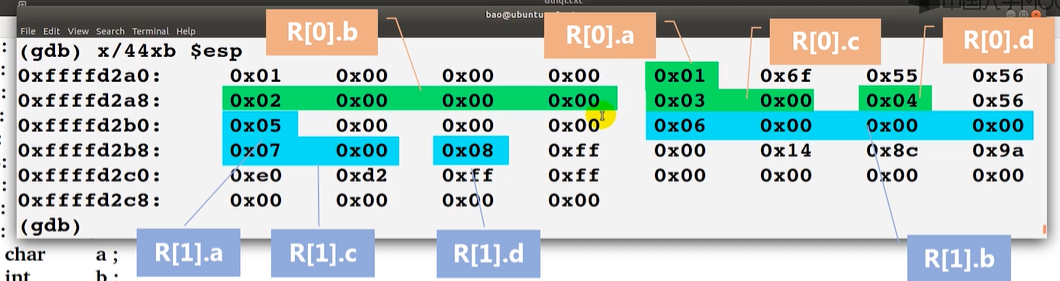


不考虑对齐方式下:数组R占用
(1+4+2+1)x2=16字节对齐方式下:数组R占用
(1+3+4+2+1+1)x2=24字节相比于不对齐,每个数组多占用 4 个字节
-
示例代码修改后
#include "stdio.h" void main() { struct record { char a; char d; short c; int b; } R[2]; R[0].a = 1; R[0].b = 2; R[0].c = 3; R[0].d = 4; R[1].a = 5; R[1].b = 6; R[1].c = 7; R[1].d = 8; printf("数据存储时的边界对齐"); } -
调试
(gdb) x/20xb $rsp 0x7ffffffeddd0: 0x01 0x04 0x03 0x00 0x02 0x00 0x00 0x00 0x7ffffffeddd8: 0x05 0x08 0x07 0x00 0x06 0x00 0x00 0x00 0x7ffffffedde0: 0xe0 0xde 0xfe 0xff
3.4数据类型的转换
3.4.1整数之间的数据类型转换
机器数之间的转换
赋值语句:b = a;
-
情况一:相同宽度的两个整型数据之间的赋值

a和b的机器数相同,真值不一定相同,取决于a和b的数据类型
-
情况二:将一个短的数据类型赋值给一个长的数据类型
-

-
把
a的n位01序列复制在b的低n位,b的高m-n位由a的数据类型决定-
n位无符号整数
-

将b的高
m-n位置为0 -
n位带符号整数
-

将b的高
m-n位置为 a 的符号位
-
-
-
情况三:将一个长的数据类型赋值给一个短的数据类型

- 将
a的低m位的01序列赋值给b,丢弃a的高位部分
-
示例代码
#include "stdio.h" void main() { short si = -100; unsigned short usi = si; int i = usi; unsigned ui = usi; int i1 = si; unsigned ui1 = si; int i2 = 0x12348765; short si2 = i2; unsigned short usi2 = i2; int i3 = si2; int i4 = 4294967296; printf("si=%d,usi=%u,i=%d,ui=%u,i1=%d,ui1=%u\n", si, usi, i, ui, i1, ui1); printf("i2=%d,si2=%d,usi2=%u,i3=%d,i4=%d\n", i2, si2, usi2, i3, i4); } -
调试
-
相同宽度的两个整型数据之间的赋值示例

-
零扩展代码示例
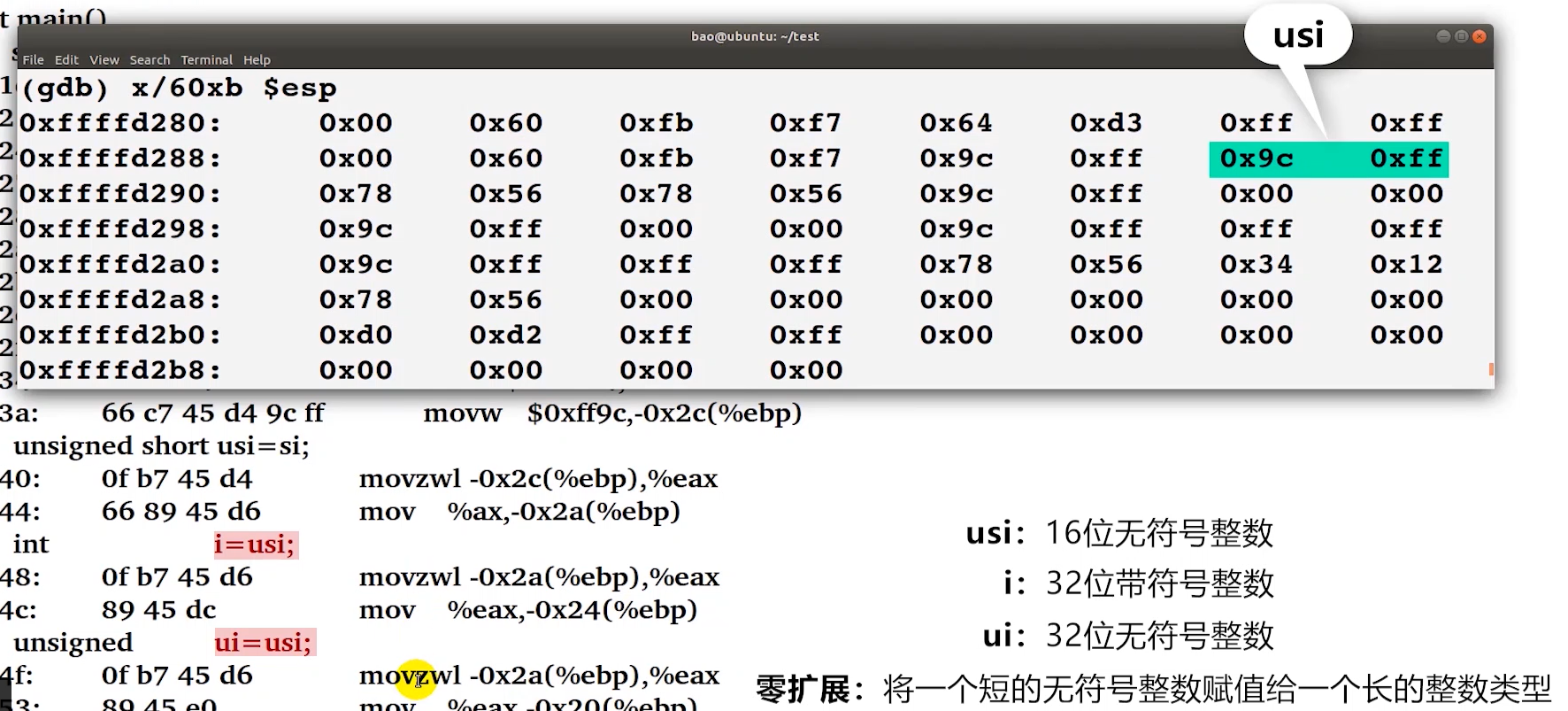
-
符号扩展示例
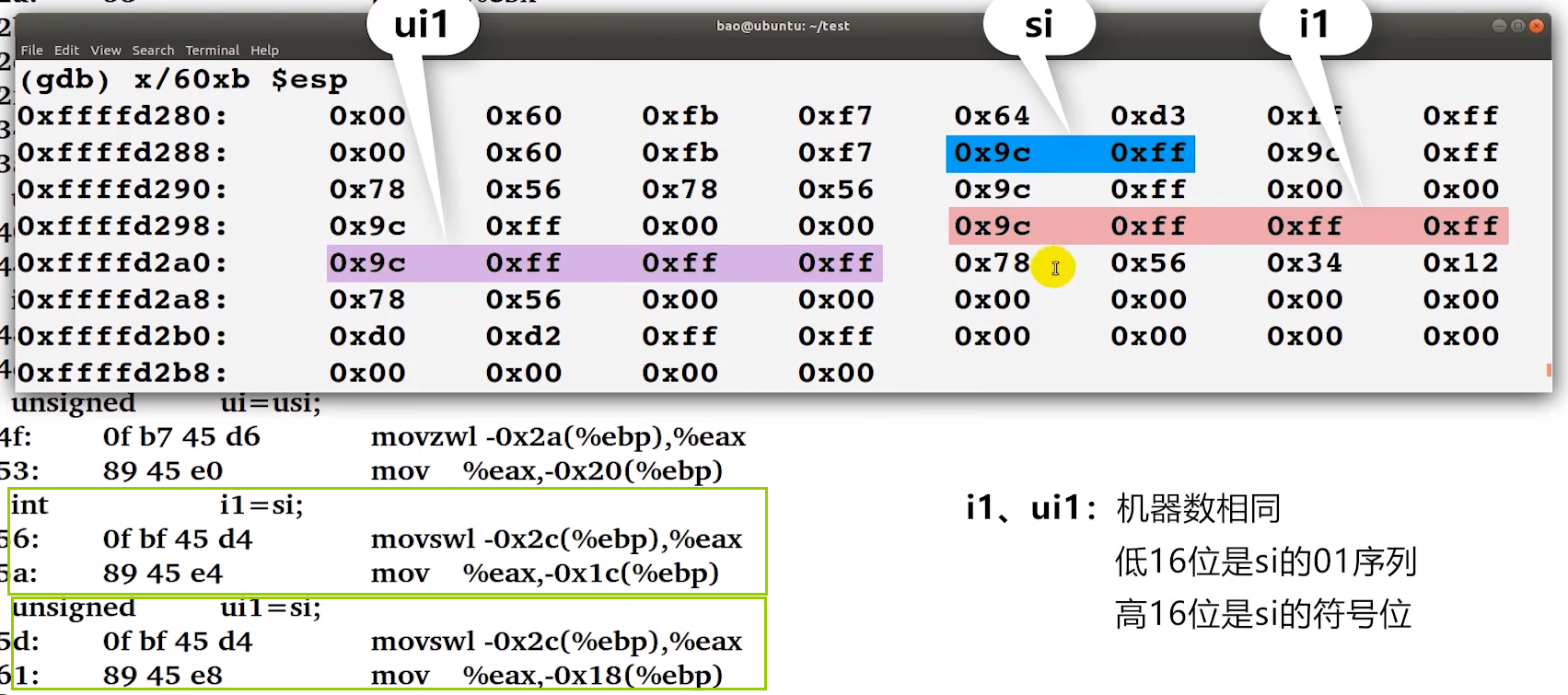
-
截断
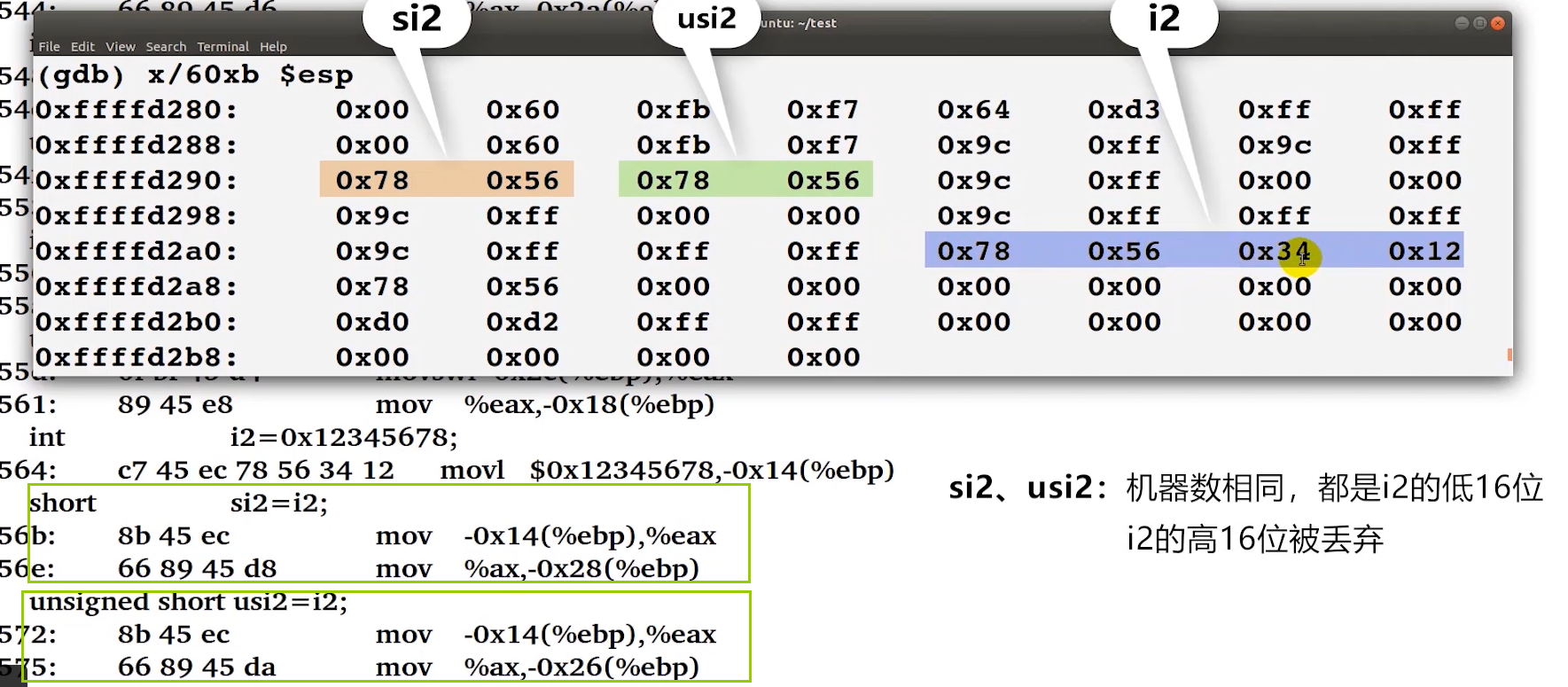
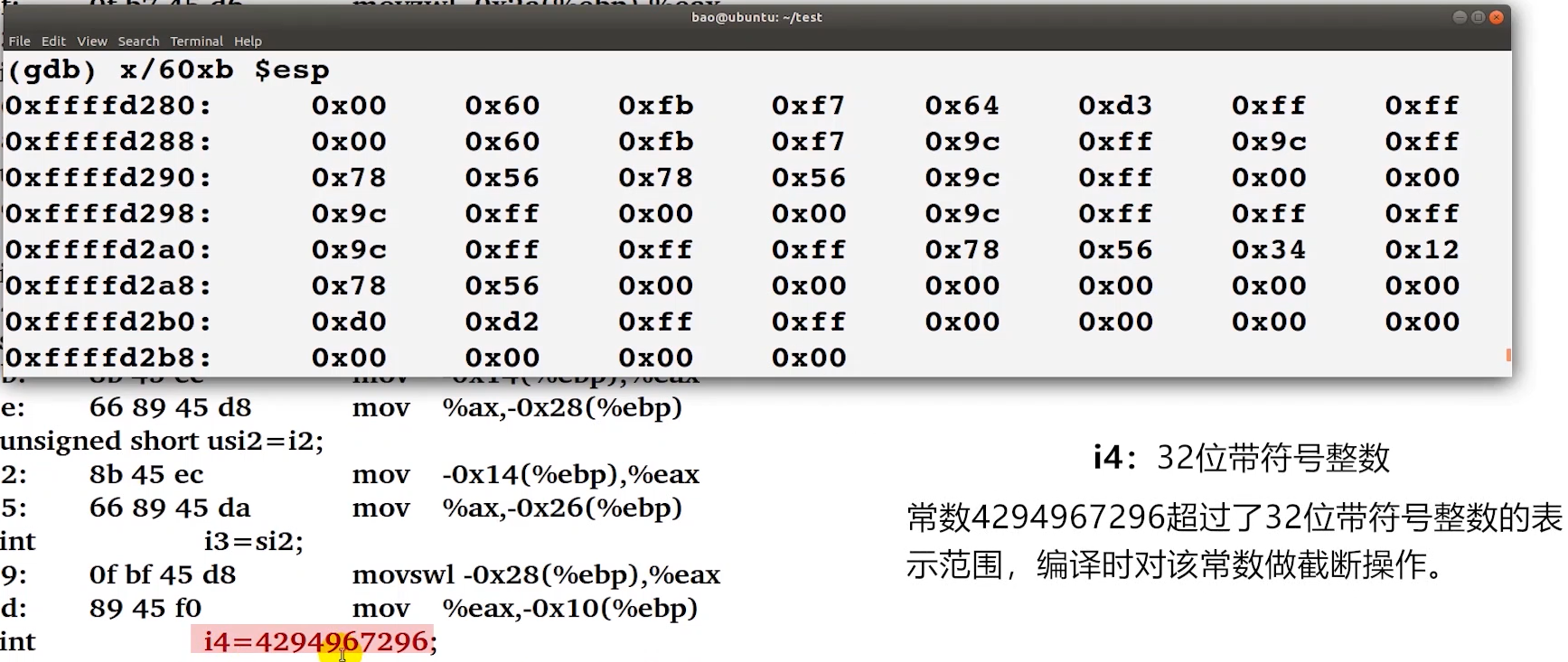
-
3.4.2整数与浮点数之间的转换
-
示例代码
#include<stdio.h> int main() { int i1=0x7fffffff,i2,itemp; float f1=0x987654321,f2,ftemp; ftemp = i1; i2 = ftemp; itemp = f1; f2 = itemp; printf("i1=%d,i2=%d,f1=%f,f2=%f\n",i1,i2,f1,f2); return 0; } -
整数到浮点数
要进行数据编码格式上的转换,而不是机器数上的直接复制。


没看太明白😕
-
浮点数到整数

3.4.3自动类型转换
-
示例代码
#include<stdio.h> int f1(unsigned int n) { int sum = 1,power = 1; int i; for(i = 0;i <= n - 1;i++) { power *= 2; sum += power; } return sum; } int main() { int sum; sum = f1(0); printf("sum=%d\n",sum); return 0; } -
执行后结果:死循环

关键在于这儿的比较,
i于n - 1的比较会自动转换为无符号整型的比较,执行完n - 1后,n的数值(edx)如下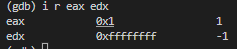
这个数在无符号整型的比较下恒成立,所以为死循环
-
修改内容
#include<stdio.h> int f1(int n)//改为整型 { int sum = 1,power = 1; int i; for(i = 0;i <= n - 1;i++) { power *= 2; sum += power; } return sum; } int main() { int sum; sum = f1(0); printf("sum=%d\n",sum); return 0; }
3.5浮点数的表示和运算–IEEE 754
3.5.1 IEEE 754 浮点数基本格式
-
float类型,32 位的单精度浮点格式
-
double类型,64 位的双精度浮点格式
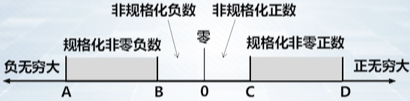
3.5.2 IEEE 754 数据按置的分类(float 为例)
- 分类五类,下图没有体现的是无定义数
-
各类值的编码
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Utc5JczA-1684569046231)(…/软件杯-高性能分析型连接查询/image-20220627151052118.png)]
-
真值与机器数对应关系举例
-
规格化数

-
非规格化数

-
-
示例程序
#include "stdio.h" void main() { float finf1 = 4e38,finf2 = 5e38,finf3 = 6e38; //正无穷大 float fninf1 = -4e38, fninf2 = -5e38, fninf3 = -6e38; //负无穷大 float fzero = 0, fnzero = -fzero;// 0,-0 float fnormal1 = 5.0, fnormal2 = 0.1, fnnormal1 = -5, fnnormal2 = -0.1; //规格化数 float ffrac = 1e-40, fnfrac = -1e-40;//非规格化数 float fnan1 = finf1 + fninf1, fnan2 = -fnan1;//无定义数 float finf4 = fnormal1 / fzero; //除以0,无穷大 printf("%f %f %f\n", finf1, finf2, finf3); printf("%f %f %f\n", fninf1, fninf2, fninf3); printf("%f %f\n", fzero, fnzero); printf("%f %.20f \n%f %.20f\n", fnormal1, fnormal2, fnnormal1, fnnormal2); printf("%.50f\n%.50f\n", ffrac, fnfrac); printf("%f %f\n", fnan1, fnan2); printf("%f \n", finf4); } -
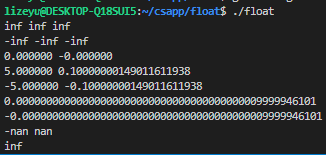
输出
-
打印结果分析
-
第一行

-
第二行

-
第三行

-
第四行

-
第五行

-
第六行

-
第七行
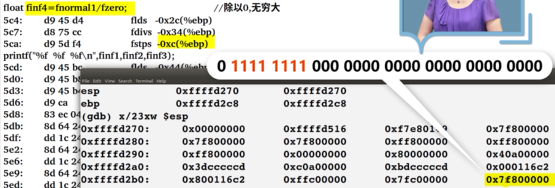
-
3.6浮点数的表示和运算–尾数的舍入处理
-
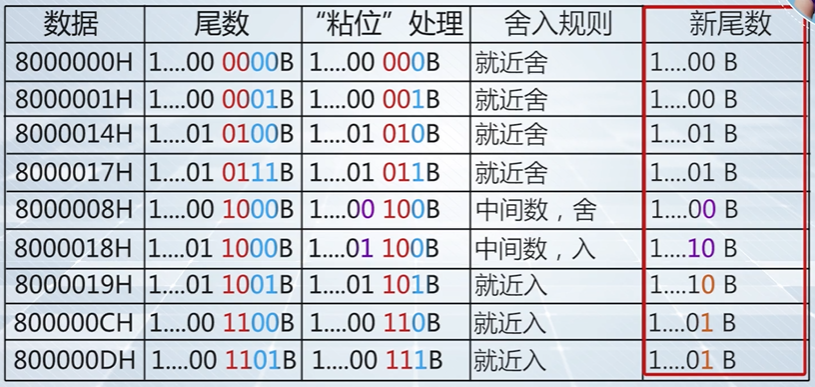
以32位单精度浮点数格式为例(就近舍入法)

-
示例代码
#include <stdio.h> void main() { float a1 = 0x8000000, a2 = 0x8000001, a3 = 0x8000014, a4 = 0x8000017; float b1 = 0x8000019, b2 = 0x800000c, b3 = 0x800000d; float c1 = 0x8000008, c2 = 0x8000018; float g = 0.1; printf("a1=%xH,a2=%xH,a3=%xH,a4=%xH\n",(int)a1,(int)a2,(int)a3,(int)a4); printf("b1=%xH,b2=%xH,b3=%xH\n",(int)b1,(int)b2,(int)b3); printf("c1=%xH,c2=%xH\n",(int)c1,(int)c2); printf("g=%.20f",g); }; -
编译运行
./floatround a1=8000000H,a2=8000000H,a3=8000010H,a4=8000010H b1=8000020H,b2=8000010H,b3=8000010H c1=8000000H,c2=8000020H g=0.10000000149011611938a1. a2、a3、a4:输出值 ≤ 初始值, 舍操作
b1、b2、b3:输出值 > 初始值, 入操作
c1:输出值 < 初始值, 舍操作
c2:输出值 > 初始值, 入操作
g:输出值> 0.1, 0.1用机器数不可以精确表示,入操作 -
分析
-