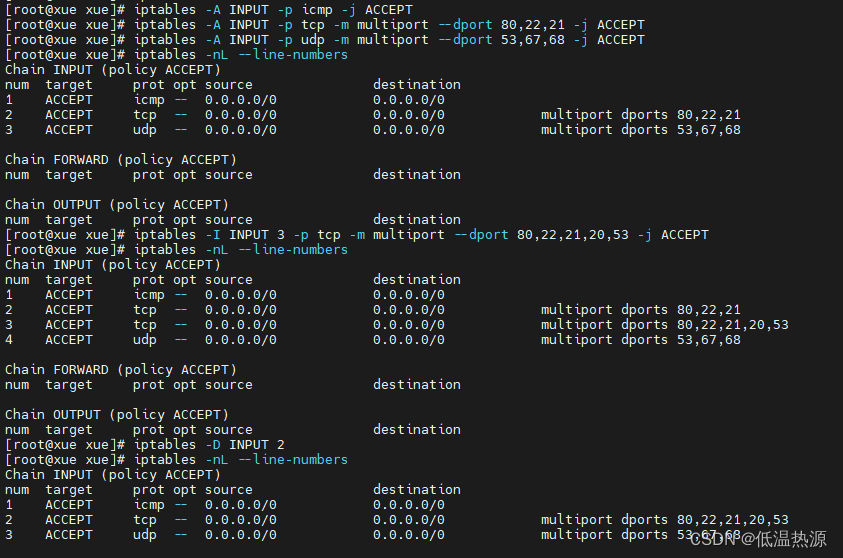
大家好呀，我是一个SLAM方向的在读博士，深知SLAM学习过程一路走来的坎坷，也十分感谢各位大佬的优质文章和源码。随着知识的越来越多，越来越细，我准备整理一个自己的激光SLAM学习笔记专栏，从0带大家快速上手激光SLAM，也方便想入门SLAM的同学和小白学习参考，相信看完会有一定的收获。如有不对的地方欢迎指出，欢迎各位大佬交流讨论，一起进步。
目录
1.做个游戏深刻理解SLAM问题
2.基于滤波的SLAM问题
2.1 贝叶斯概率
2.2 贝叶斯滤波
2.3 粒子滤波
2.3 求解SLAM问题
3. 基于图优化的SLAM
3.1 图
3.2 最小二乘算法
3.3 最小二乘求解
3.4 基于图优化的SLAM框架
1.做个游戏深刻理解SLAM问题
首先我们先来玩一个游戏，猜猜我在哪？
下图选取我们学校的地图，只给你说我在学校里，那么请你猜一猜我在哪？
你应该会说，我在学校的任何一个地方，且是等概率的。
下面我给自己规定我开始行走了，每一步是70cm，每次转身是90° ，我给你说我开始移动了，并且给你发了一张我附近环境的照片。这时你会觉得我在操场附近周围的概率很大，但学校有三个操场，你还是不知道我具体位置。
我走了100步给你说我看到了宿舍楼在我前方，你会认为我在下图深色区域的概率比较大，但学校有三个宿舍区，你还是不知道我具体位置。
我向左走了500m，看到了体育馆我在右边，这时你可以更精确的定位到我大概的位置，因为满足这样有体育馆和宿舍区方位的路径只能是这一条。但还是一个大概的区域，不能精确定位。
这时我又给你说，我向右转走50步到体育馆门口了，你可以更加精确的定位我在体育馆门口的某处，并且你估计出我行走的路径如下图的右下角所示。
但是我自己本身走路是不可能走直线的，并且转向时也不能保证自己一定是90°，所以目前你估计的路径和真实我走的路径是存在差异的。但是如果我每走一步都给你精确的周围环境信息和距离，我相信你是可以很精确的估计出我的位姿变化和路径的。
好了游戏到此结束，上述的游戏证明了两点
- 位姿估计问题靠自己的估计是不够的，就像我设定自己每一步是70cm，但不可能每一步都走70cm一点不差。
- 位姿估计的过程似乎和概率有点关系，上述游戏从开始的整个九龙湖为可能空间到最后的几个点。
2.基于滤波的SLAM问题
2.1 贝叶斯概率
上述游戏让我们觉得位姿估计过程好像和概率有关，那么既然说到了概率问题，我们就从最常用的抛硬币问题说起，让你预测下一次正面反面的概率是多少？你会说正反，反面各0.5呗，大家都知道，没错是这样。
下面增加难度了，我让你估计一下明天股票是涨还是跌，给你整不会了，这谁知道，这要是我知道了，我就不上学炒股了。那为什么抛硬币容易估计，估计股票就难呢？这是因为股市是一个随机过程，随机过程：研究的随机变量之间不独立，由于不独立，无法做随机实验，难度较高。
随机实验需要满足3个条件：
①相同条件下，可重复进行；
②一次试验，结果不确定，但所有结果已知（比如抛硬币，要么正要么反，所有结果已知）；
③试验之前，结果未知。
换句话说，你想如果你想在相同条件下做股市实验，除非时间倒流。很多跟时间有关系的都是随机过程，比较难以估计（做重复实验），例如股市、温度、位姿估计——预测问题。
那好，你不知道怎么估计了，我们看一下股市大佬是怎么估计股票涨跌的。他们会每天看各种新闻，搜寻各种各样的外界信息来判断明天股市的涨跌情况。
比如你初始估计股票涨跌的概率是各0.5，但你看到今天特斯拉刹车失灵了，那么你肯定会觉得明天特斯拉股票大概率是跌。
到这里你会觉得，这个估计股市的涨跌和估计位姿咋似乎有点像呢？没错，这就是贝叶斯概率，贝叶斯概率的核心思想就是先验概率根据外部观测得到后验概率。
2.2 贝叶斯滤波
贝叶斯公式的的推导如下所示：
为了加深理解，再举一个测温度的小例子
这样你知道这类概率估计问题如何求解了，主体就是自己不会，就找外界信息。下面让你估计这一天的温度，你会说这有啥难的，我每一时刻都进行一次贝叶斯公式的计算，先估计一个概率，再根据外界观测修正。但你会觉得每次估计有点麻烦吧，如果我就第一次温度的先验是估计，得到后验估计，将这个后验估计当做下一时刻的先验估计以此类推，这样我整个过程不就只需要开始自己估计一次，后续都是自动的多米诺骨牌一样。太棒了同学，你自己推出了贝叶斯滤波。
上图就是贝叶斯滤波的过程和公式，贝叶斯滤波虽然能够解决这类问题，但大多数情况下没有解析解，因为需要做无穷积分，那怎么求解呢?
2.3 粒子滤波
粒子滤波的核心思想就是用一堆粒子来近似概率密度，从而避免无穷积分，看下图你会觉得咋和咱们的游戏越来越有种说不出来的关系。
粒子滤波相比于贝叶斯滤波的区别是，它需要选择粒子，并且用粒子去传播的，那么如何高效的采样粒子是一个重要的问题。
下图就用咱们之前的游戏很简单的说明了一下如何选择高效的例子，初始采样，权重评估和重采样。假设游戏只让你选择81个点去猜我所在的位置，一开始你只能平均选择位置点，在我发来一张操场照片后，让你再选择81个点，你肯定会在操场周围选择。
总结一下选粒子的过程：
2.3 求解SLAM问题
好了，现在我们知道位姿变换问题要用到贝叶斯滤波迭代，并且引入了粒子滤波来方便求解，这下子我们终于可以求解SLAM问题了。
以惯性测量作为初始的先验估计，用激光雷达的观测信息来修正得到后验位姿，这就是最初的SLAM系统——Fast-SLAM。后续大名鼎鼎的Gmapping算法在Fast-SLAM的基础上，进行了内存爆炸优化和粒子耗散优化，具体什么操作大家搜一下，我写累了hhh。
Gmapping是一个基于2D激光雷达使用RBPF（Rao-Blackwellized Particle Filters）算法完成二维栅格地图构建的SLAM算法，适用于室内小范围SLAM。
优点：gmapping可以实时构建室内环境地图，在小场景计算量少，且地图精度较高，对激光雷达扫描频率要求较低。
缺点：随着环境的增大，构建地图所需的内存和计算量就会变得巨大，所以gmapping不适合大场景构图。一个直观的感受是，对于200x200米的范围，如果栅格分辨率是5cm，每个栅格占用一个字节内存，那么每个粒子携带的地图都要16M的内存，如果是100粒子就是1.6G内存。
但由于用滤波去求解永远都无法消除上述的三个红色问题，SLAM就进入了图优化时代。
3. 基于图优化的SLAM
3.1 图
首先介绍什么是图，用一个图(Graph)来表示SLAM问题，图中的节点来表示机器人的位姿，两个节点之间的边表示两个位姿的空间约束。
Graph-based SLAM：构建图，并且找到一个最优的配置(各节点的位姿)，让预测与观测的误差最小。
图优化的过程就像是织一个好看的蜘蛛网。图优化核心思想：误差不是突然来的，而是和整个过程都有关系，需要整体调整一下找到全局最优，保证总误差最小。
全局最优这个词是不是有点熟悉，这不就是我们的最小二乘算法所解决的问题吗？没错图优化SLAM的求解思想还真是用的最小二乘算法，只不过是非线性的。
3.2 最小二乘算法
我们最早应该在高中接触过最小二乘算法，用于直线拟合。如果将每个点看成位置，曲线看成路径，这不就SLAM位姿估计了嘛。
说起来简单做起来难啊，线性的我会求解，那非线性的最小二乘问题咋求解嘞。
3.3 最小二乘求解
3.4 基于图优化的SLAM框架
总结一下基于图优化：考虑了移动载体历程中全部的位姿状态和环境观测信息，用节点和边形成的图来表示一系列的移动机器人位姿和约束，建立和维护关联数据，可独立出前端实现并行计算，是一种更为高效和普适的优化方法。一般分为扫描匹配、闭环检测、后端优化、点云地图存储。
我自己根据理解，画了一下现在广泛使用的激光SLAM系统，如有不对请指正。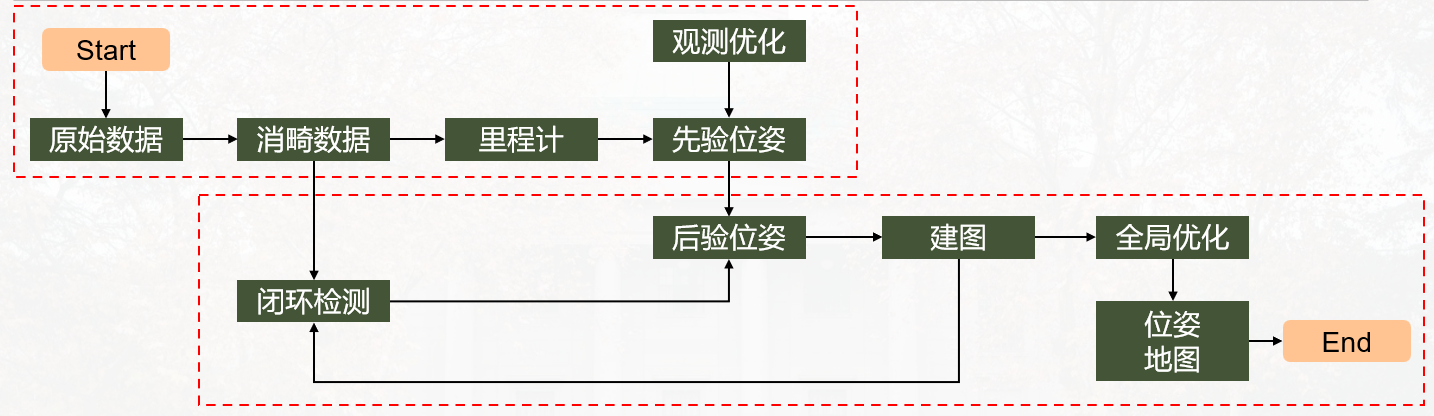
到此，你了解了SLAM的前世今生了，下一节我将针对SLAM系统的每一块进行讲解，之后再结合Lego-loam源码进行讲解。如果内容对你有用的话，请订阅本专栏吧，免费哦~
