💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

💥1 概述

📚2 运行结果

​

🎉3 参考文献

🌈4 Matlab代码实现

---

💥1 概述

高效实施基于集群化电压控制的重要前提就是合理的分布式能源集群划分，现有的分布式能源集群常常根据地域界限、网络拓扑等形成，不同的集群内电压调节常常对其他集群的节点电压影响较大，或是集群内部电压调节效率较低，大大减小了电压调节的效率。

因此，合理的分布式能源集群划分，使集群内部耦合紧密，集群间耦合较松，实现集群间近似解耦，具有较大的实际意义。

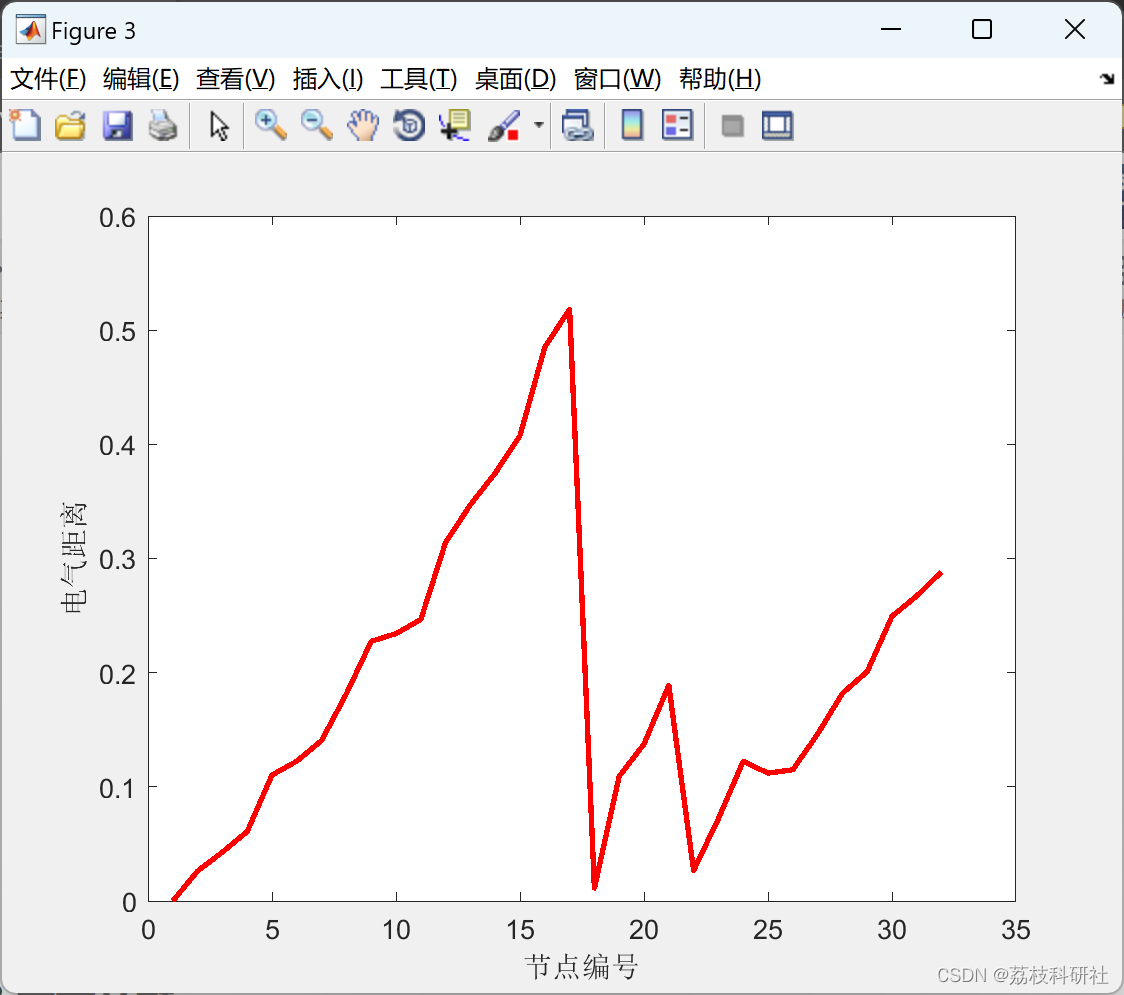
集群划分的最初目的是基于某一特征，将相似的个体划分至同一集群，将不同的个体的划分至不同集群。本文中集群划分的目标是电压控制，基于电压对功率变化的灵敏程度，使对互相灵敏度较高的划分至同一集群，将互相灵敏度较弱的分至不同集群，从而使得电压调节策略能够在集群内部有效实施，而对集群外部的影响较小。由第 3 章分析，分布式能源网络中的有功、无功对节点电压都有影响，且显然不同节点间的电压影响各不相同，初步考虑利用某节点注入功率变化对其它节点影响程度大小来定义电气距离。基于上述分析，采用节点电压对其余各节点注入功率变化的灵敏度[17]来定义节点之间电气距离。由 3.4.1 中的式（3-18）~（3-20）可以求出各节点间的电压-有功灵敏度矩阵和节点间的电压-无功灵敏度矩阵SQ。

灵敏度系数越大，节点注入功率变化对电压变化影响越大，即节点间电气距离越近，因此，记：

但是，由于在实际配电网络中，并不只是节点间两两互联，使得两节点距离不止和自身节点有关，还与周围其它节点的相关。而且一般情况下，两个节点之间有且仅有一个电气距离值，即满足：

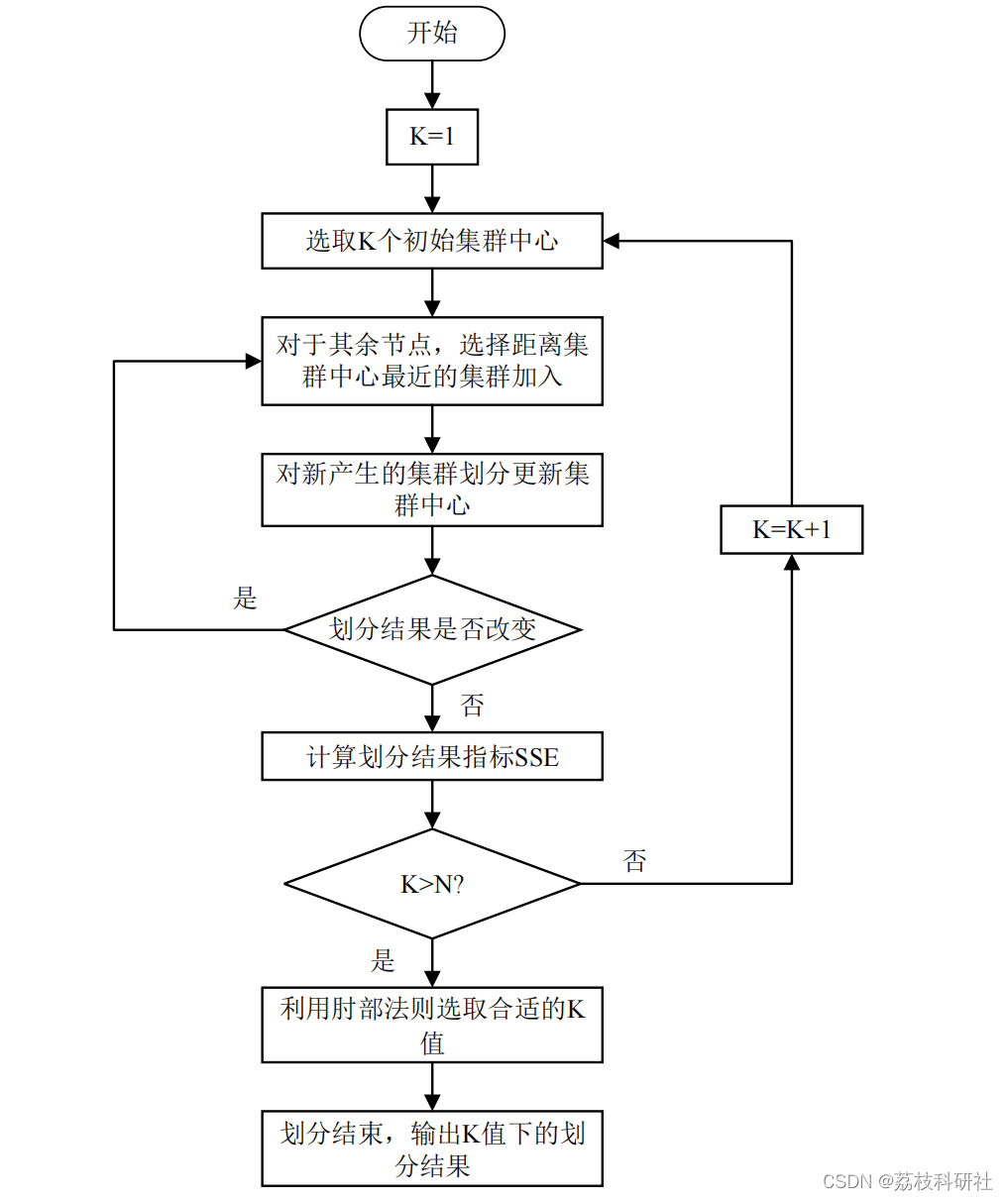
结合上述分析，基于电压调节的集群划分方式流程如图所示。 

📚2 运行结果

 

 

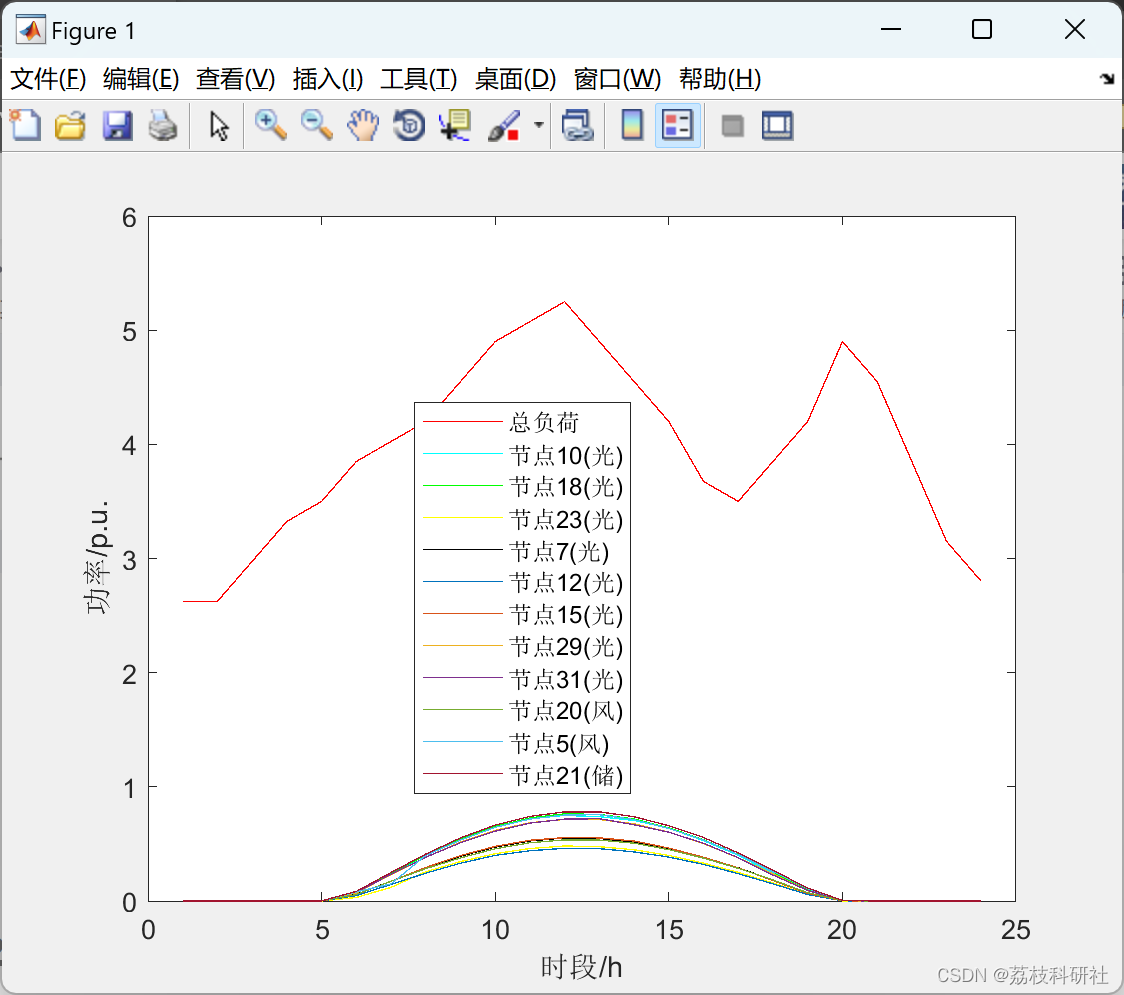
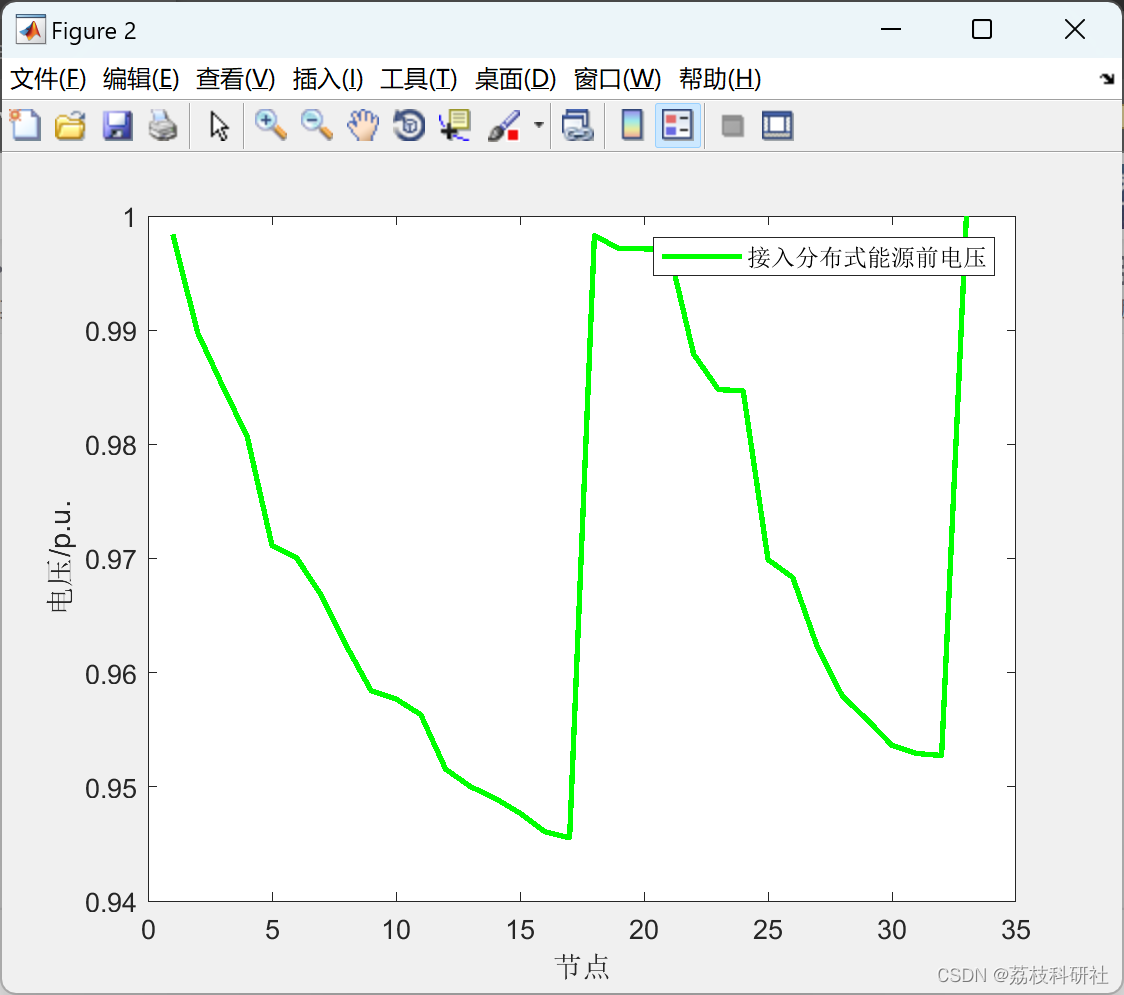
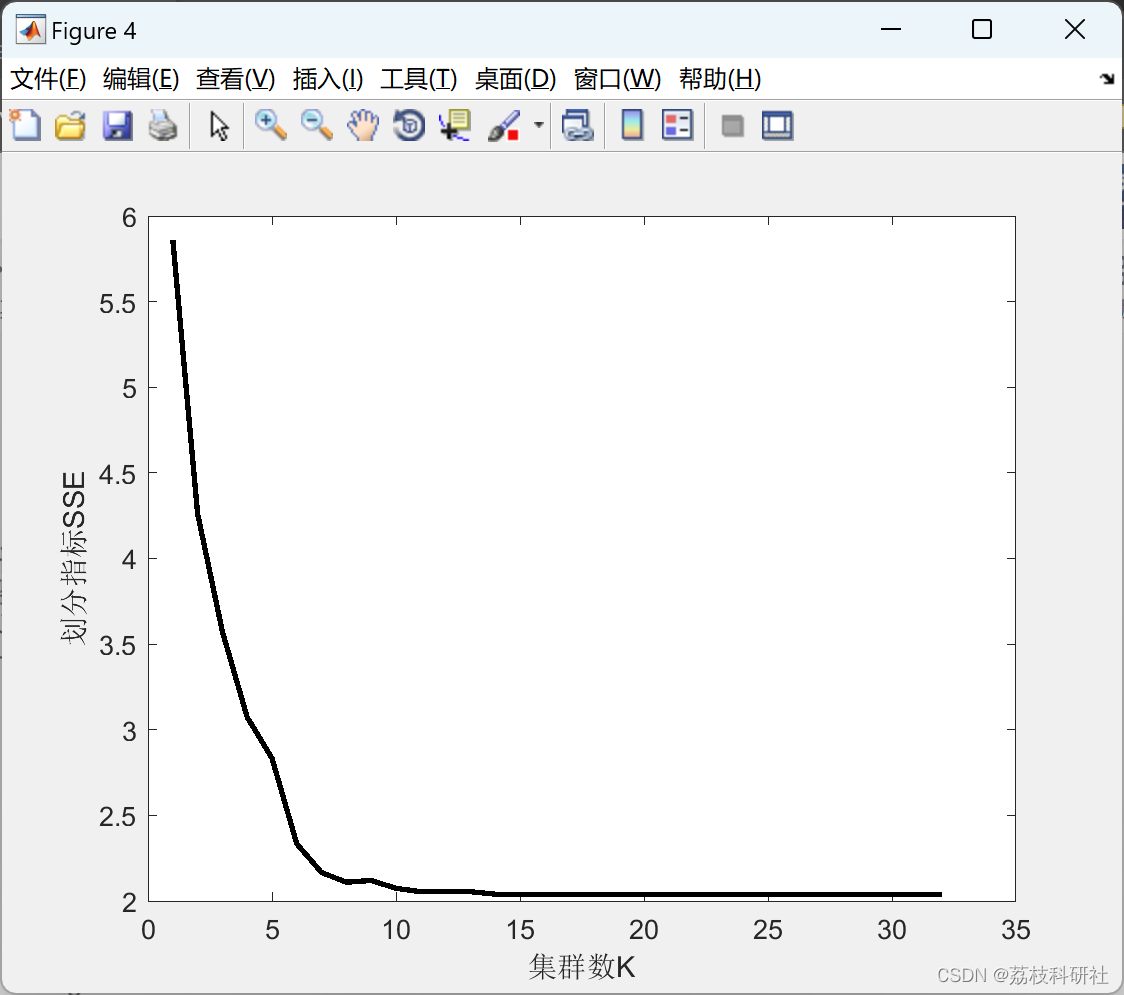
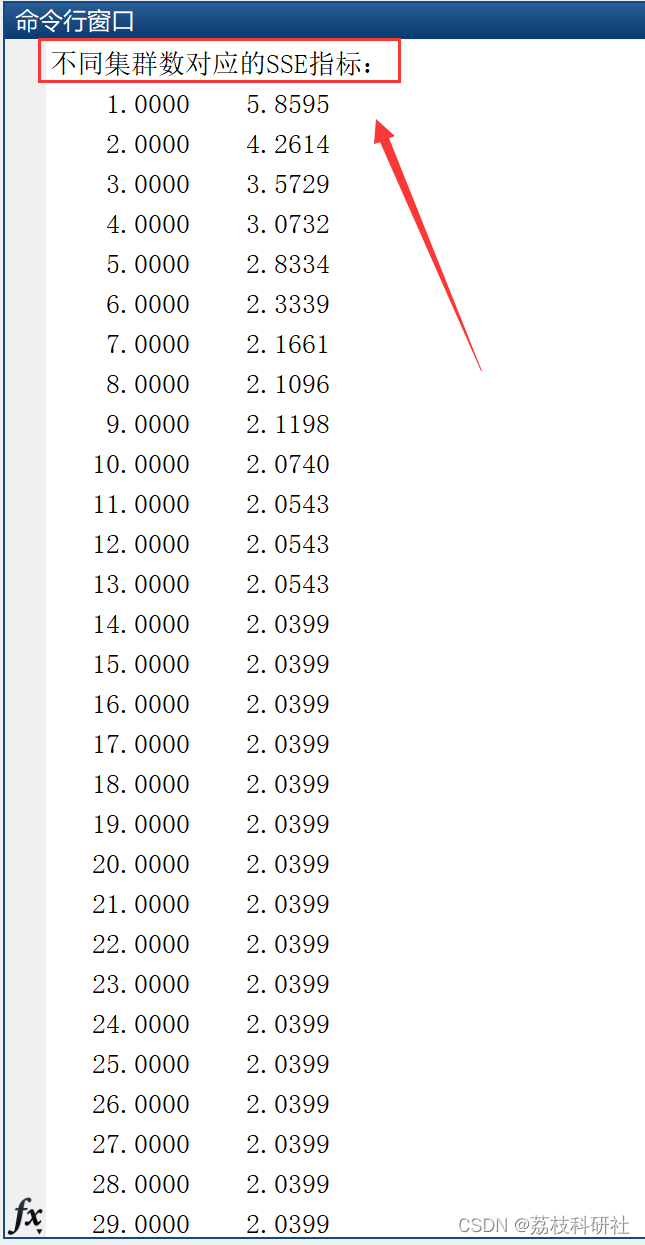
不同集群数对应的SSE指标：
    1.0000    5.8595
    2.0000    4.2614
    3.0000    3.5729
    4.0000    3.0732
    5.0000    2.8334
    6.0000    2.3339
    7.0000    2.1661
    8.0000    2.1096
    9.0000    2.1198
   10.0000    2.0740
   11.0000    2.0543
   12.0000    2.0543
   13.0000    2.0543
   14.0000    2.0399
   15.0000    2.0399
   16.0000    2.0399
   17.0000    2.0399
   18.0000    2.0399
   19.0000    2.0399
   20.0000    2.0399
   21.0000    2.0399
   22.0000    2.0399
   23.0000    2.0399
   24.0000    2.0399
   25.0000    2.0399
   26.0000    2.0399
   27.0000    2.0399
   28.0000    2.0399
   29.0000    2.0399
   30.0000    2.0399
   31.0000    2.0399
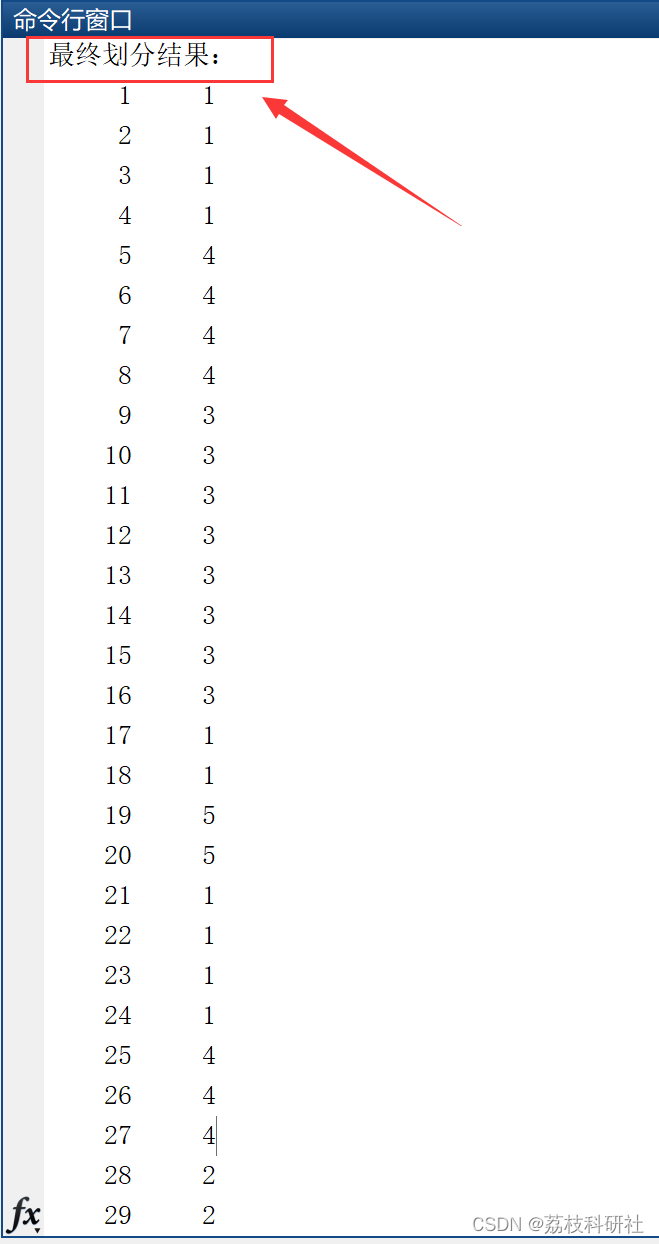
   32.0000    2.0399

最终划分结果：
     1     1
     2     1
     3     1
     4     1
     5     4
     6     4
     7     4
     8     4
     9     3
    10     3
    11     3
    12     3
    13     3
    14     3
    15     3
    16     3
    17     1
    18     1
    19     5
    20     5
    21     1
    22     1
    23     1
    24     1
    25     4
    26     4
    27     4
    28     2
    29     2
    30     2
    31     2
    32     3

🎉3 参考文献

部分理论来源于网络，如有侵权请联系删除。

[1]尉同正,杜红卫,夏栋,韩韬,吴雪琼,徐政.基于改进K-means算法的分布式发电集群划分方法[J/OL].华北电力大学学报(自然科学版):1-9[2023-05-19].http://kns.cnki.net/kcms/detail/13.1212.TM.20230217.1641.004.html

[1]黄秋红,王霄,杨靖,范圆成.基于集群划分的区域短期风电功率预测模型[J].电力科学与工程,2022,38(12):8-17.

🌈4 Matlab代码实现