第三弹来啦,第一章的顺序表和链表落下帷幕了,可以开开心心吃雪糕了:)
beautiful分割线
文章目录
- 第三弹来啦,第一章的顺序表和链表落下帷幕了,可以开开心心吃雪糕了:)
- 循环链表
- 定义
- 带尾指针循环链表的合并
- 双向链表
- 定义
- 双向循环链表
- 双向链表的插入
- 双向链表的删除
- 链表的时间效率比较
- 顺序表和链表的比较
- 线性表的应用
- 线性表的合并
- 有序表的合并
- 案例分析
- 连续性多项式求和运算
- 稀疏多项式运算
循环链表
定义
-
头尾相连的链表,最后一个节点的指针域指向头结点,形成一个环。
-
优点是从任一节点出发均可找到其他节点。
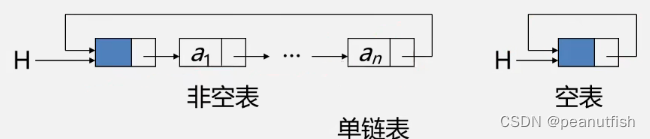
- 注意:循环链表没有NULL指针,判断遍历终止操作时,终止条件是判断他们是否等于头指针

- 通常用尾指针表示单循环链表,方便对尾结点和头节点操作

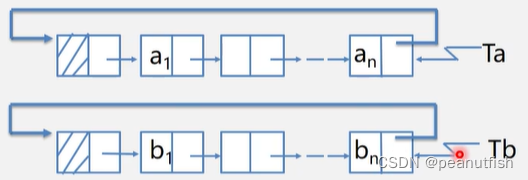
带尾指针循环链表的合并
将Tb合并在Ta之前
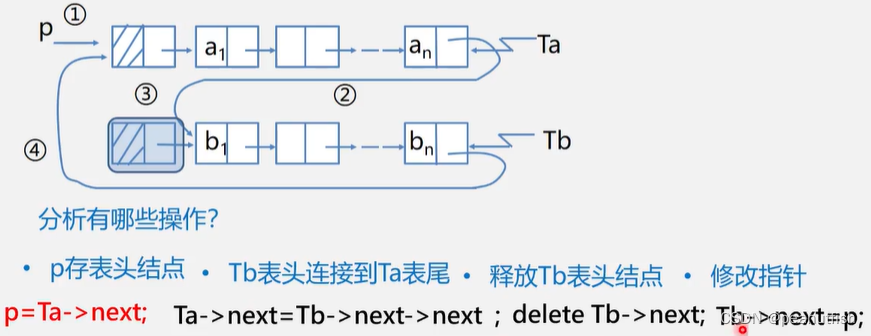
LinkList Connect(LinkList Ta, LinkList Tb){
//假设Ta,Tb都是非空的单循环链表
p=Ta->next; //p存表头节点
Ta->next=Tb->next->next; //Tb表头连接Ta表尾
delete(p); //释放Tb头结点(free(Tb->next))
Tb->next=p; //修改Tb->指针到新头结点
return Tb;
}
双向链表
定义
在单链表的每个节点中再增加一个指向其前趋的指针域prior, 这样就有了两个方向的链接,称为双向链表,(也解决单链表中寻找前驱结点难的情形)。
| prior | data | next |
|---|
- 结构定义:
typedef struct DuLnode{
Elemtype data;
struct DuLnode *prior, *next;
}DuLnode, *DuLinkList;

-
双向链表的对称性(假设p指向某一节点)
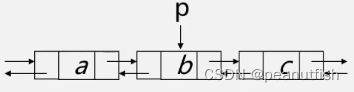
p->prior->next = p = p->next->prior -
双向链表中的某些操作,如果只涉及到一根指针(ListLength, GetElem…),则他们的算法和单链表相同,但是插入,删除操作需要同时修改两个方向上的指针,操作时间复杂度O(n).
双向循环链表
- 头结点的前趋指向尾结点
- 尾结点的后继指向头结点

双向链表的插入
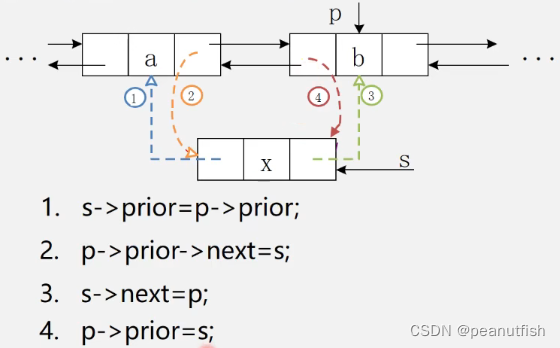
void LinkInsert_DuL(DuLinkList &L,int i, ElemType e){
//在带头结点的双向链表L中第i个位置插入元素e
if(!(p=GetElemP_DuL(L,i))) return ERROR;
s=new DuLnode; s->data=e; //创建新节点s并赋值
s->prior=p->prior; //s节点的前趋指向
p->prior->next=s; //a节点的后继指向
s->next=p; //s节点的后继指向
p->prior=s; //b节点的前趋指向
return OK;
}//ListInsert_DuL
双向链表的删除
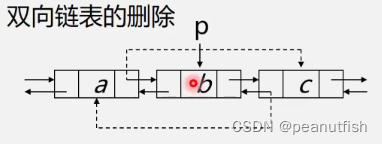
Void ListDelete_DuL(DuLinkList &L, int i, ElemType &e){
//在双向链表中删除i位置元素
if(!(p=GetElemP_DuL(L,i))) return ERROR;
e = p->data; // 保存被删数据
p->prior->next = p->next; // 修改前一个节点后继
p->next->prior = p->prior; // 修改后一个节点的前趋
delete(p);
return OK;
}//ListDelete_DuL
链表的时间效率比较
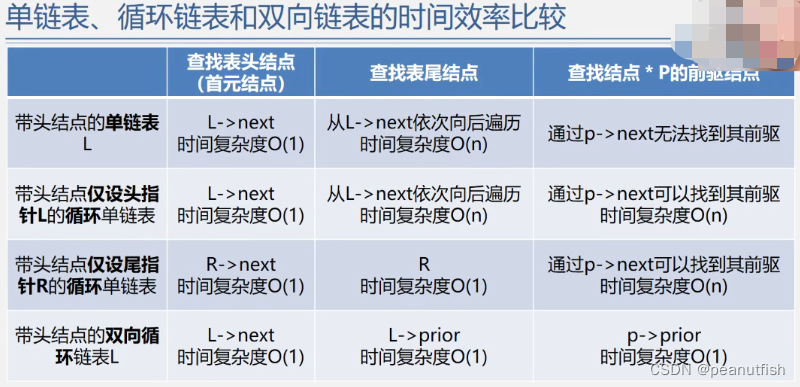
顺序表和链表的比较

线性表的应用
线性表的合并
两个线性表La, Lb 分别表示两个集合A,B,现在要求一个新的集合A=AUB
La=(7,5,3,11) Lb=(2,6,3) ==> La=(7,5,3,11,2,6)
算法步骤:
依次取出Lb中的每个元素,执行以下操作:
- 在La中查找该元素
- 如果找不到,则将其插入La的最后
- 算法的时间复杂度:
O(ListLength(La)*ListLength(Lb))
void union(List &La, List Lb){
La_len=ListLength(La);
Lb_len=ListLength(Lb);
for (i=1;i<=Lb_len;i++){
GetElem(Lb,i,e);
if (!LocateElem(La,e)) ListInsert(&La,++La_len,e)
}
}
有序表的合并
一致线性表La, Lb中的数据元素按值非递减有序排列,现将两表合并成一个新表Lc, 且要求Lc中的元素仍按值非递减有序排列。(非递减:有值相等的,非完全的递增)
La=(1,7,8) Lb=(2,4,6,8,10,11) ==> Lc=(1,2,4,6,7,8,8,10,11)
用顺序表算法步骤:
(1)创建一个空表Lc
(2)依次从La或Lb中"摘取“元素值较小的结点插入到Lc表的最后,直至其中一个表变空为止
(3)继续将La或Lb其中一个表的剩余结点插入在Lc表的最后
(4)算法的时间复杂度和空间复杂度均为 O(ListLength(La)+(ListLength(Lb))
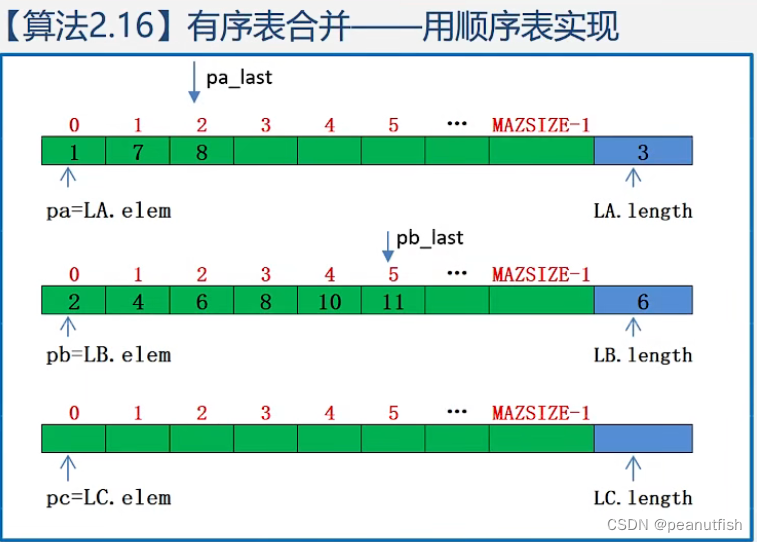
// 顺序表实现有序表的合并(非递减排序)
void MergeList_Sq(SqList La, SqList Lb, SqList &Lc){
pa=La.elem; //La基地址
pb=Lb.elem; //Lb基地址
Lc.length=La.length+Lb.length; //Lc的长度
Lc.elem=new ElemType[Lc.length]; //创建新表Lc并分配数组空间
pc=Lc.elem;
pa_last=La.elem+La.length-1; //last指针是指向表中最后一个元素,用于循环摘取时确认表中数据是否读完
pb_last=Lb.elem+Lb.length-1;
while (pa<=pa_last && pb<=pb_last) { //两表非空
if (*pa<=*pb) *pc++ = *pa++; //依次摘取两表中较小元素放入Lc
else *pc++ = *pb++;
}
while (pa<=pa_last) *pc++ = *pa++; //Lb为空时,将La中剩余元素加到Lc
while (pb<=pb_last) *pc++ = *pb++; //La为空时,将Lb中剩余元素加到Lc
}//MergeList_Sq
用链表算法步骤
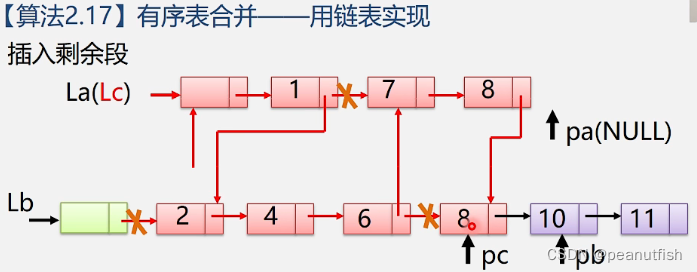
// 链表实现有序表的合并(非递减排序)
void MergeList_L(LinkList &La, LinkList &Lb, ListList, &Lc) {
pa=La->next; pb=Lb->next;
pc=Lc=La; // Lc在La的基础上变身(使用La的头节点),当然也可以用Lb头结点
while (pa&&pb){
if (pa->data <= pb->data) {pc->next=pa; pc=pa; pa=pa->next;}
else {pc->next=pb; pc=pb; pb=pb->next;} //比较La和Lb中的元素大小,将小的元素接到Lc上,并移动相应指针到下一个位置
}
if pc->next=pa?pa:pb; //三目运算符用于将La/Lb中剩余的元素加到Lc上,pa存在取pa,pa不存在取pb
delete Lb; //删除Lb头结点
}
// 时间复杂度为O(ListLength(La)+(ListLength(Lb))
案例分析
连续性多项式求和运算
数组形式解决 - 保存系数,指数和下标相同
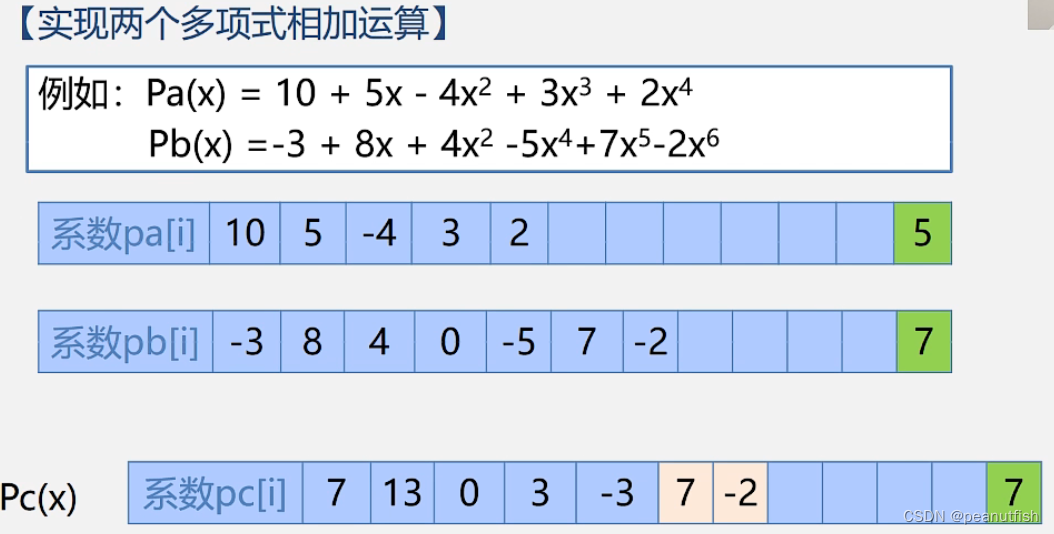
稀疏多项式运算

- 顺序表思想

- 链表思想
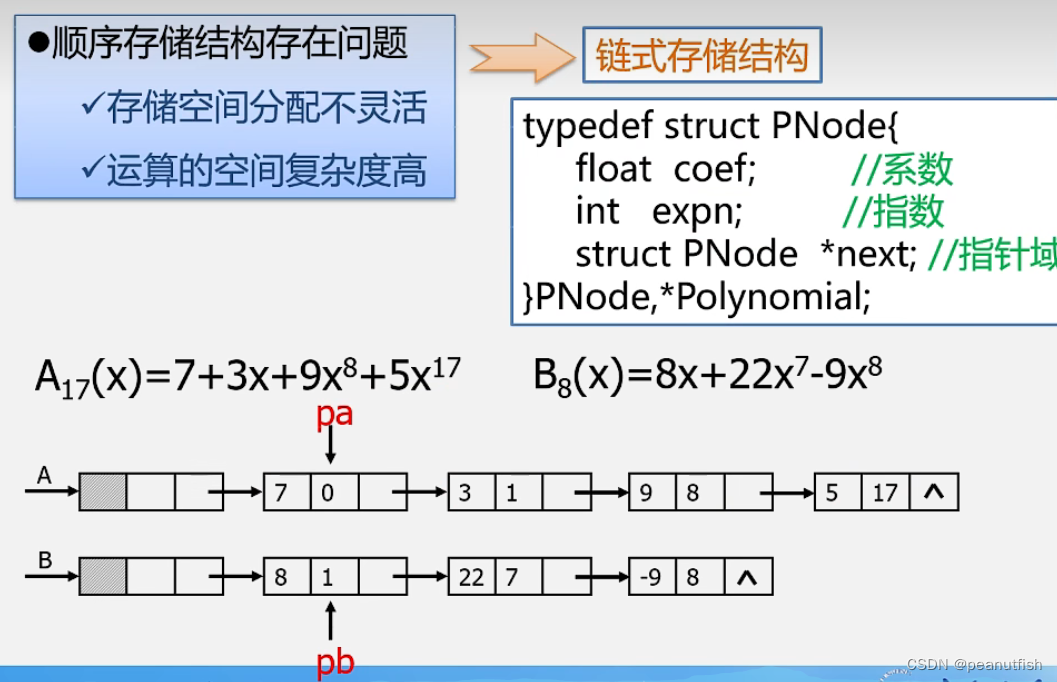

//多项式的创建 - 链式存储
void CreatePolyn(Polynomial &P, int n) { //输入元素想输n,创建多项式有序列表P
P=new PNode;
P->next=NULL; // 建立一个带头结点的空的单链表
for (i=1;i<=n;i++){ //依次输入n个非零项
s=new PNode; // 生成新节点
sin>>s->coef>>s->expn; // 输入新节点的系数和指数
pre=P; //pre用于保存q的前驱,初值为头结点
q=P->next; //q初始化,指向首元结点
while (q && q->expn<s->expn) { // 循环找到第一个大于s节点指数的项
pre=q; q=q->next
}
s->next=q; // 将输入项s节点插入到q和前驱结点pre之间
pre->next=s;
}
}
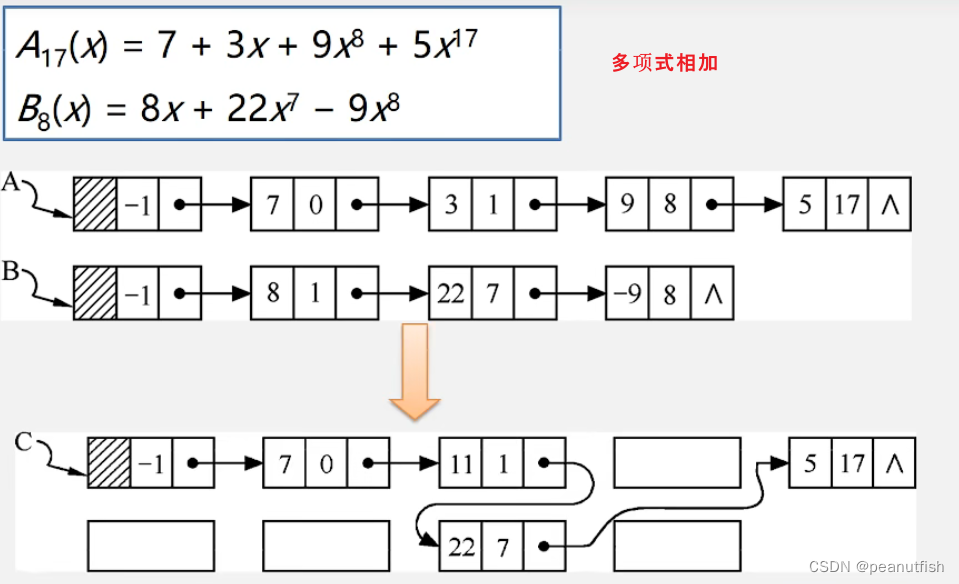
采用链表合并的思想

//链表思想 - 多项式求和运算
void Add_Polyn(Polynomial &Pa, Polynomial &Pb, Polynomial &Pc){
p1=Pa->next; p2=Pb->next; //p1,p2指向两个链表的首元结点
p3=Pc=Pa; // 基于Pa的头结点创建和初始化链表Pc
PNode *s; // 创建一个临时指针s用于后面删除节点
while(p1 && p2){ // 在p1,p2不为空的前提下,循环比较两个节点的指数大小
if (p1->expn < p2->expn){ // p1指数小于p2指数情况
p3->next=p1; p3=p1; p1=p1->next; // 把p1加入到p3中,p1移向下一个节点
} else if (p1->expn > p2->expn) { // p1指数大于p2指数情况
p3->next=p2; p3=p2; p2=p2->next; // 把p2加入到p3中,p2移向下一个节点
} else { // p1指数等于p2指数情况
p1->coef += p2->coef; // p1和p2两者系数相加并放到p1节点中
if (!p1->coef) { // 系数相加为0时,删除这两个节点
s=p1;p1=p1->next; delete(s); //此处不能直接free(p),不然链表会断开的
s=p2;p2=p2->next; delete(s);
}
else {
p3->next=p1;p3=p1; p1=p1->next; // 系数相加不为0时,将新系数的节点p1加入P3中,删除p2节点
s=p2;p2=p2->next; delete(s);
}
}
}
if p3->next=p1?p1:p2; delete p2; // 将p1或者p2中剩下的不用比较系数的节点直接加到p3中
}
TO BE CONTINUED…