1. 背景

在大数据点云的存储中，常常要进行空间分区，一般的策略是构建四叉树或者八叉树。在构建树的过程中，一个不可避免的点就是点云的快速抽稀。

不同层级之间，下一层的数据永远比上一层的数据更加精细，即：上一层数据是从下一层通过某种抽稀算法筛选出来的。常规意义上的抽稀算法，是在内存中进行筛选，但由于大数据点云的特殊性（无法全部读进内存），这些抽稀算法均不满足要求，存在一下问题：

无法全部读进内存，因此抽稀之后不同分块（分块策略是前提）的效果不一；
抽稀效率比较低，需要预先将数据读进内存，再进行分层筛选；

某项目中，需要将*.las转换成自定义格式，其转换速率要求很高。而由于las文件在使用LASTools读写时，只能逐点读取，因此需要一种既能解决上述问题，又能保证效率的抽稀算法。

本文介绍的抽稀算法，原理上是利用伪随机数的均匀分布来实现，但同时能兼顾效率和效果。其局限性如下：

随机数表是存储在内存中，因此数据量过大的情况下，内存占用可能会很高；
抽稀效率随C++标准库的随机数生成算法影响；
数据量很小的时候，存在某层数据为空的可能；

2. 原理

基于以下出发点：

每读一个点，能立即得到该点所属层级——las的逐点读限制；
las文件只需读一次，就能得到抽稀结果——O(n),n为点数；
保证抽稀结果均匀——加入随机数；

对于第一点，将las文件中的顶点数据，类比成一个存储了顶点的数组：

v	v	v	v	v	v	v	v	v	v	v	v	v	v	v	v	…

LASTools的读操作器每一次读取的时候，都会将游标移到下一个点。对每一个点来说，本身并没有层级信息，因此需要人为地赋予其层级。

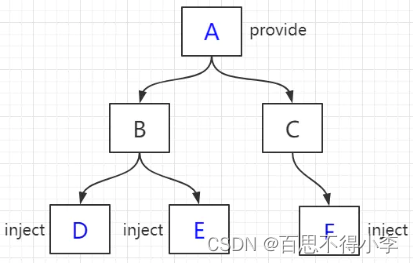
计算层级可以类比分类游戏：一堆小球从入口进入，中间穿插阻碍棒，最终落到容器内：

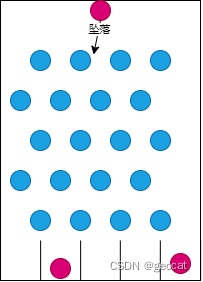
而将红色小球理解为点云的顶点，将下面的容器理解为结果，则中间的蓝色小球是我们的抽稀算法。

核心原理就是，每次获取一个随机数，这个随机数的值就是当前点所在的层级。而随机数的范围，就是按照n叉树的层级点数比例，计算出来的一个值。具体实现见后文。

3. 实现

3.1 定义Utils类

class Utils
{
private:
    Utils(int lvl);
    ~Utils();

public:
    static Utils &instance();
    int getLayer();

protected:
    char *m_lvl;
    int m_l;
};

3.2 加入预定义宏，确定层级

#ifndef DEFAULT_LEVEL_COUNT
#define DEFAULT_LEVEL_COUNT 7
#endif

3.3 函数实现

const std::size_t g_num[10] = {
    1, 4, 16, 64, 256, 1024, 4096, 16384, 65536, 262144};
const std::size_t g_sum[10] = {
    1,
    1 + 4,
    1 + 4 + 16,
    1 + 4 + 16 + 64,
    1 + 4 + 16 + 64 + 256,
    1 + 4 + 16 + 64 + 256 + 1024,
    1 + 4 + 16 + 64 + 256 + 1024 + 4096,
    1 + 4 + 16 + 64 + 256 + 1024 + 4096 + 16384,
    1 + 4 + 16 + 64 + 256 + 1024 + 4096 + 16384 + 65536,
    1 + 4 + 16 + 64 + 256 + 1024 + 4096 + 16384 + 65536 + 262144,
};

Utils::Utils(int lvl)
{
    m_lvl = new char[g_sum[lvl - 1]];

    std::size_t idx = 0;
    for (int i = 0; i < lvl; ++i)
    {
        std::size_t tms = g_num[i];
        // for (int j = 0; j < tms; ++j)
        // {
        //     m_lvl[idx + j] = (char)i;
        // }
        std::fill_n(m_lvl + idx, tms, (char)i);
        idx += tms;
    }
    m_l = lvl;
}

Utils::~Utils()
{
    delete[] m_lvl;
}

Utils &Utils::instance()
{
    static Utils s_ret(DEFAULT_LEVEL_COUNT);
    return s_ret;
}

int Utils::getLayer()
{
    static std::default_random_engine s_dre;
    static std::uniform_int_distribution<unsigned long> s_uid(g_sum[0], g_sum[m_l - 1]);

    return (int)(m_lvl[s_uid(s_dre)]);
}