题目描述

题目链接：[LeetCode 1769]移动所有球到每个盒子所需的最小操作数

有 n 个盒子。给你一个长度为 n 的二进制字符串 boxes ，其中 boxes[i] 的值为 ‘0’ 表示第 i 个盒子是空的，而 boxes[i] 的值为 ‘1’ 表示盒子里有一个小球。

在一步操作中，你可以将一个小球从某个盒子移动到一个与之相邻的盒子中。第 i 个盒子和第 j 个盒子相邻需满足 abs(i - j) == 1 。注意，操作执行后，某些盒子中可能会存在不止一个小球。

返回一个长度为 n 的数组 answer ，其中 answer[i] 是将所有小球移动到第 i 个盒子所需的最小操作数。

每个 answer[i] 都需要根据盒子的初始状态进行计算。

示例1

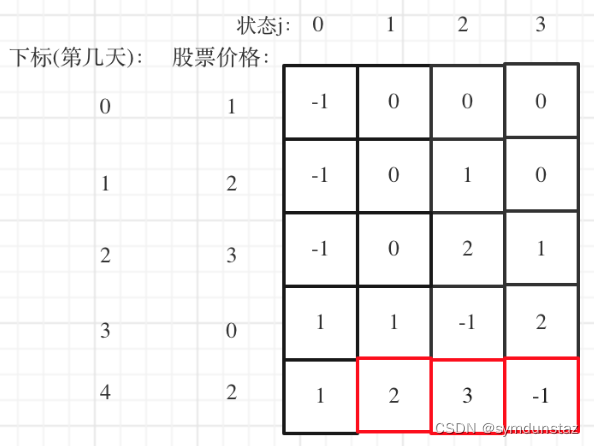
输入：boxes = “110”
输出：[1,1,3]
解释：每个盒子对应的最小操作数如下：

第 1 个盒子：将一个小球从第 2 个盒子移动到第 1 个盒子，需要 1 步操作。
第 2 个盒子：将一个小球从第 1 个盒子移动到第 2 个盒子，需要 1 步操作。
第 3 个盒子：将一个小球从第 1 个盒子移动到第 3 个盒子，需要 2 步操作。将一个小球从第 2 个盒子移动到第 3 个盒子，需要 1 步操作。共计 3 步操作。

示例2

输入：boxes = “001011”
输出：[11,8,5,4,3,4]

提示

n == boxes.length
1 <= n <= 2000
boxes[i] 为 ‘0’ 或 ‘1’

思路分析

1.boxes.length <= 2000，那么如果算法复杂度为O（ $n^2$ ）,大约为 $10^6$ ，是可以暴力通过的，这是方法1

2.那么要在 $n^2$ 的基础上进行突破，就需要将复杂度降低到O(n log n)或者O(n)的级别

我们可以从左右两个方向来讨论，首先是左侧，如图所示，假如当前遍历到了红色结点，这个结点的坐标为i，他的左边有两个结点：

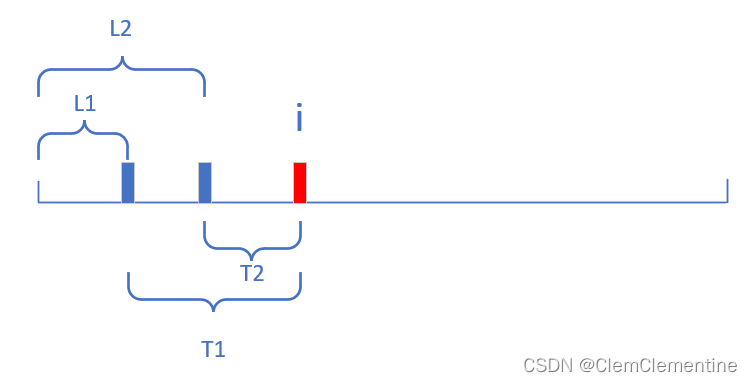
在这里插入图片描述
那么把左边两个结点都移动到i位置所需要的代价就是T1 + T2

T1 与 T2不好计算，所以我们计算两个结点到左端点的距离，L1 和 L2

而L1 + T1 = i， L2 + T2 = i,

因此T1 + T2 = 2 * i - (L1 + L2)

依次类推要计算T1 + T2 + … + Tn = n * i - (L1 + L2 + L3 + … + Ln)

所以我们记录每个时刻的(L1 + L2 + … + Ln) 以及 n为多少，就可以计算左边所有结点到当前结点的代价了。

同理，右侧结点也是一样。

代码1（暴力）

class Solution {
public:
    vector<int> minOperations(string boxes) {
        int n = boxes.size();
        vector<int> res(n);
        unordered_set<int> st;
        for(int i = 0; i < n; i++) {
            if(boxes[i] == '1') st.insert(i);
        }

        for(int i = 0; i < n; i++) {
            int cnt = 0;
            for(auto t : st) {
                cnt += abs(t - i);
            }
            res[i] = cnt;
        }

        return res;
    }
};

代码2

class Solution {
public:
    vector<int> minOperations(string boxes) {
        int n = boxes.size();
        //l[i]存储i结点左边所有结点到i的代价，r[i]同理
        vector<int> l(n), r(n), res(n);
        int cnt = 0, len = 0;
        for(int i = 0; i < n; i++) {
            l[i] = i * cnt - len;
            //如果当前结点为1,那么len要加上i，同时结点数++
            if(boxes[i] == '1') len += i, cnt++;
        }

        cnt = 0, len = 0;
        for(int i = n - 1; ~i; i--) {
            r[i] = (n - i - 1) * cnt - len;
            if(boxes[i] == '1') len += (n - i - 1), cnt++;
        }

        for(int i = 0; i < n; i++) 
            res[i] = l[i] + r[i];
        return res;
    }
};