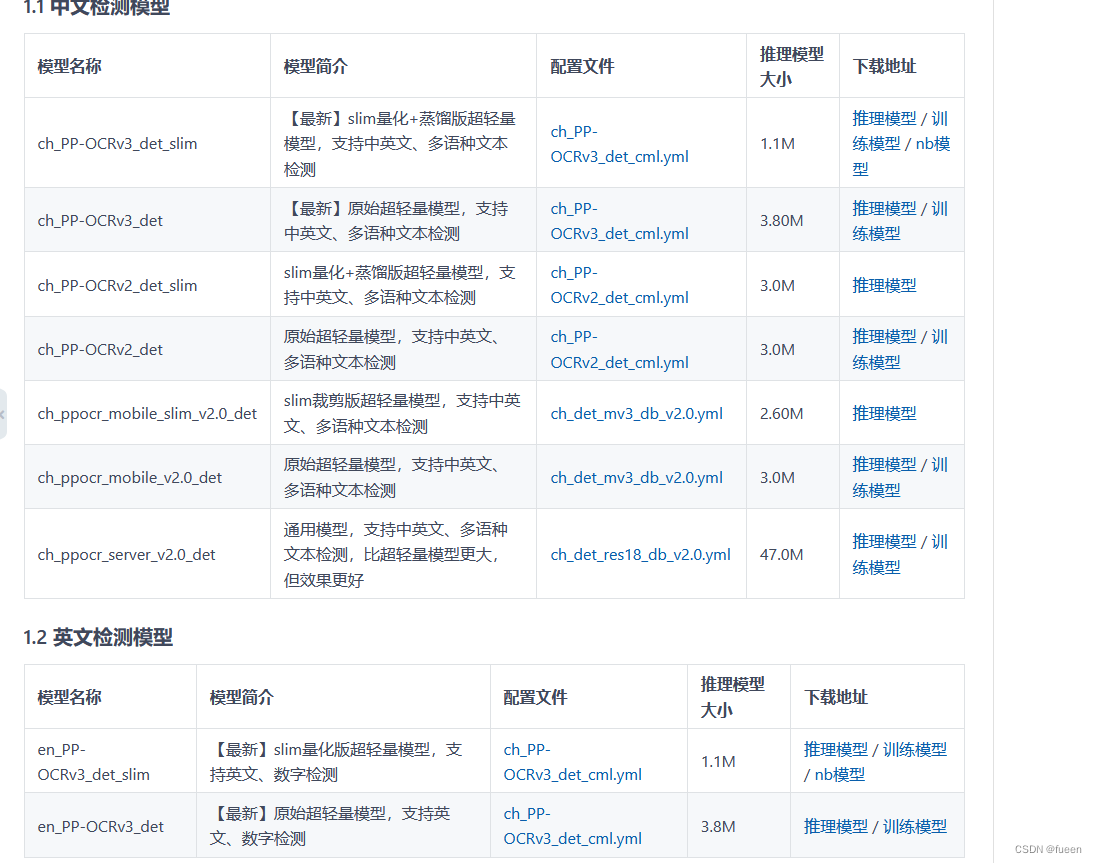
Problem - 1582D - Codeforces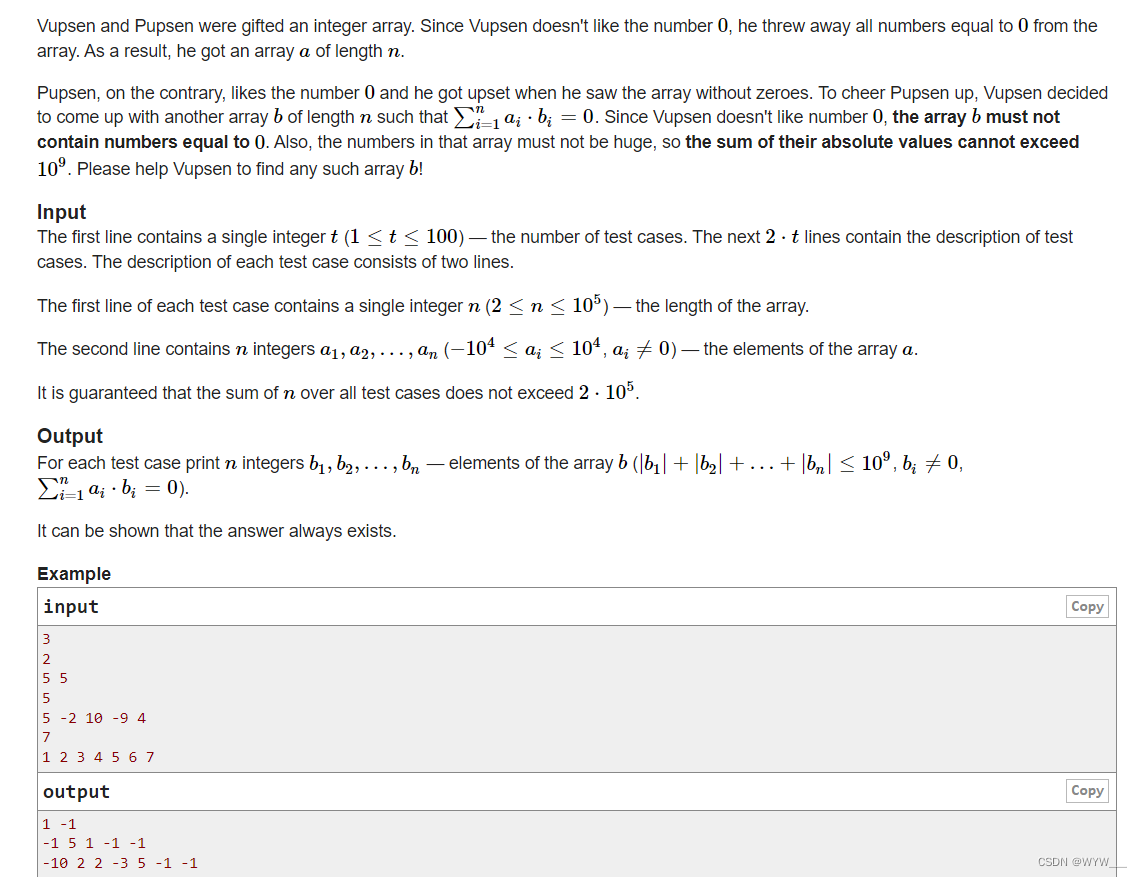

Vupsen和Pupsen被赠予一个整数数组。由于Vupsen不喜欢数字0，他把数组中所有等于0的数字都扔掉了。结果，他得到一个长度为n的数组a。

相反，Pupsen喜欢数字0，当他看到没有0的数组时，他很不高兴。为了让Pupsen高兴，Vupsen决定想出另一个长度为n的数组b，使∑ni=1ai⋅bi=0。由于Vupsen不喜欢数字0，数组b中不能包含等于0的数字。请帮助Vupsen找到任何这样的数组b!

输入
第一行包含一个整数t（1≤t≤100）--测试案例的数量。接下来的2-t行包含测试用例的描述。每个测试用例的描述由两行组成。

每个测试用例的第一行包含一个整数n（2≤n≤105）--数组的长度。

第二行包含n个整数a1,a2,...,an（-104≤ai≤104, ai≠0）--数组a的元素。

保证所有测试案例的n之和不超过2⋅105。

输出
对于每个测试案例打印n个整数b1,b2,...,bn--数组b的元素（|b1|+|b2|+...+|bn|≤109，bi≠0，∑ni=1ai⋅bi=0）。

可以证明，答案总是存在的。

例子
输入复制
3
2
5 5
5
5 -2 10 -9 4
7
1 2 3 4 5 6 7
输出拷贝
1 -1
-1 5 1 -1 -1
-10 2 2 -3 5 -1 -1
注意
在第一个测试案例中，5⋅1+5⋅(-1)=5-5=0。例如，您也可以打印3-3，因为5⋅3+5⋅(-3)=15-15=0。
在第二个测试案例中，5⋅(-1)+(-2)⋅5+10⋅1+(-9)⋅(-1)+4⋅(-1)=5-10+10+9-4=0。

题解:
从整体考虑似乎有点麻烦

那我们就从部分开始考虑

两个数之间如何构造?

a,b

-b,a

那么n为偶数的情况我们就得到了

由此再想一想

如果n为偶数呢?

我们可以发现只要构造一个为3的小块,剩下的部分就为偶数了

如何构造3个数的组呢?

a,b,c

(b+c) -a -a

但是还有一点坑,可能b+c = 0

但是不用担心三个数之间肯定有两个数相加大于0的情况,找到构造即可

#include<iostream>
#include<vector>
#include<queue>
#include<cstring>
#include<algorithm>
#include<string>
#include<map>
using namespace std;
#define int long long
int a[100040];
void solve() 
{
//	ios::sync_with_stdio(false);
//	cin.tie(0);
//	cout.tie(0);
	int n;
	cin >> n;
	for(int i = 1;i <= n;i++)
	cin >> a[i];
	if(n%2 == 0)
	{
		for(int i = 1;i <= n;i+=2)
		{
			cout<<a[i+1]<<" "<<-a[i]<<" ";
		}
		cout<<"\n";
	}
	else
	{
		if(a[2] + a[3]!=0)
		cout<<(a[2] + a[3])<<" "<<-a[1]<<" "<<-a[1]<<" ";
		else if(a[1] + a[3]!=0)
		cout<<-a[2]<<" "<<(a[1] + a[3])<<" "<<-a[2]<<" ";
		else
		cout<<-a[3]<<" "<<-a[3]<<" "<<(a[1] + a[2])<<" ";
		for(int i = 4;i <= n;i+=2)
		{
			cout<<a[i+1]<<" "<<-a[i]<<" ";
		}
		cout<<"\n";
	}

}
signed main()
{
	int t = 1;
	cin >> t;
	while(t--)
	{
		solve();
	}
}