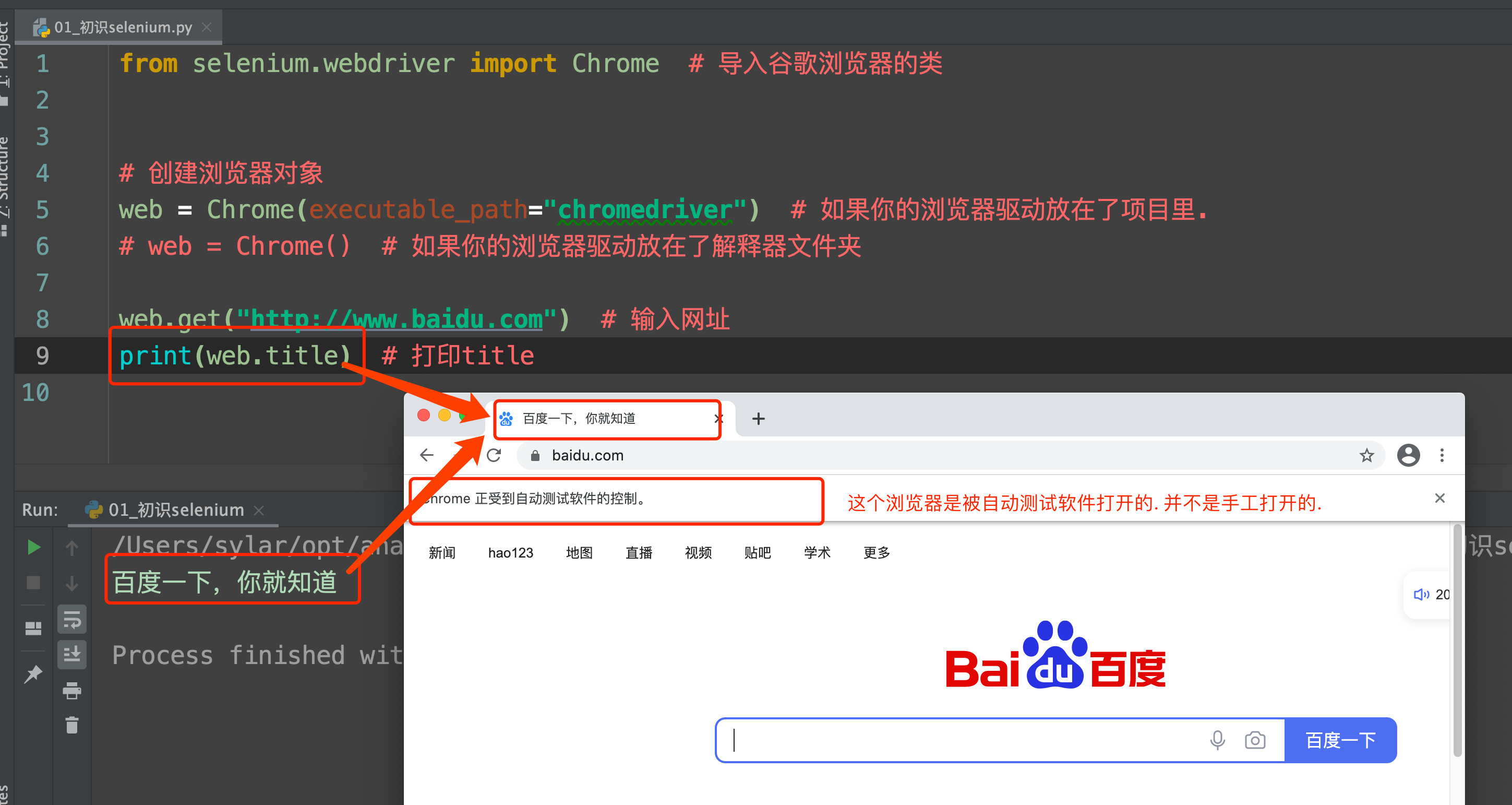
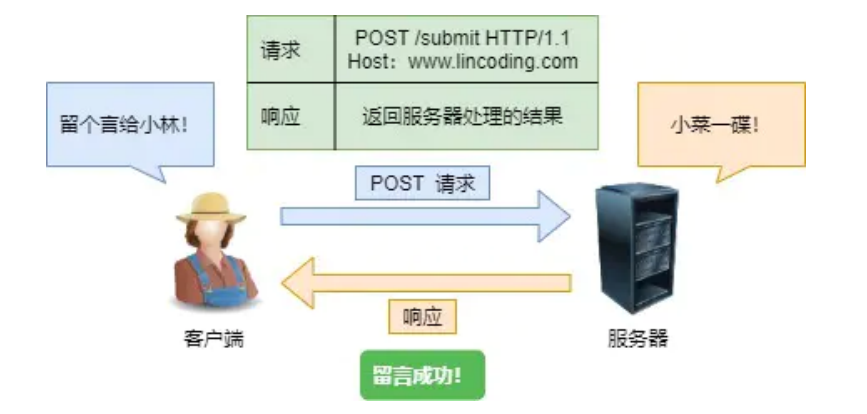
参考链接：https://www.163.com/dy/article/GK6BBSEB0531PW97.html
https://zhuanlan.zhihu.com/p/477141677

DFE全称为Decision Feedback Equalizer，即决策反馈均衡器。它是一种电信通信系统中常用的均衡器，在接收信号端实现等化器、滤波器和解调器的功能。DFE均衡器主要通过对接收信号进行反响（feedback）处理来避免多径干扰的影响。具体来说，DFE均衡器可以根据先前的决策信息，尝试预测下一个输入样本的信号状态，并使用其来提高接收信号的质量和稳定性。其运作的步骤如下：

1. 输入信号的采集：接收信号是通过天线采集到，并通过ADC转换为数字信号。
2. 前向均衡器：输入信号通过前向均衡器进行均衡，以消除来自多径干扰的影响。
3. 决策器：输入信号进入决策器中，依据已决策的信息来计算下一个输入样本的状态，并做出相应的判决。
4. 反向均衡器：由于来自决策器的判定仅准确到一定程度，因此需要通过反向均衡器进行反馈处理，来消除决策误差及抑制干扰信号。
5. 信号输出：通过输出端口输出均衡后的信号。
   DFE均衡器常用于高速数据传输系统中，以消除多径干扰，并提高信号的可靠性和稳定性。

判决反馈均衡器（Decision Feedback Equalier, DFE)，是目前SerDes中常见于于RX部分的一种均衡方式，能够有效提升RX的接收性能。

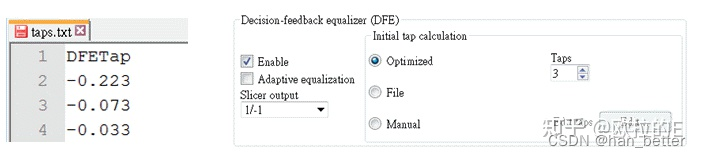
DFE 通常用于 SERDES 接收器 (RX)，以消除由有损信道引起的信号间干扰 (ISI)。 DFE 包括一个有限脉冲响应 (FIR) 滤波器、一个加法器和一个用于信号决策的切片器。 图 1 显示了一个三抽头 DFE 示例。 DFE 的优点是它可以在不放大噪声的情况下消除 ISI。 缺点是它无法纠正前向 ISI。

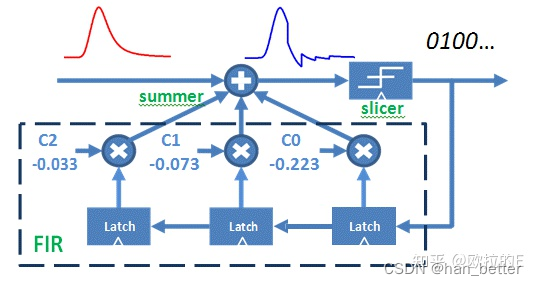
首先，使用 FIR 计算来自先前面信号的 ISI。 然后从输入信号中减去干扰。 最后，切片器做出符号判决并将信号输出回 FIR。 选择抽头值以最小化 ISI。 在此示例中，抽头值为 -0.223、-0.073 和 -0.033。 图 2 显示后信号采样点的干扰被去除。

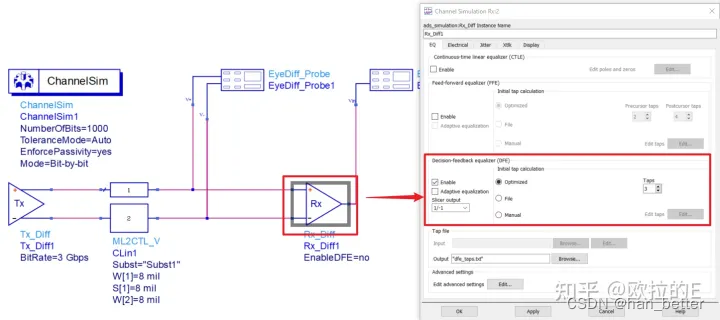
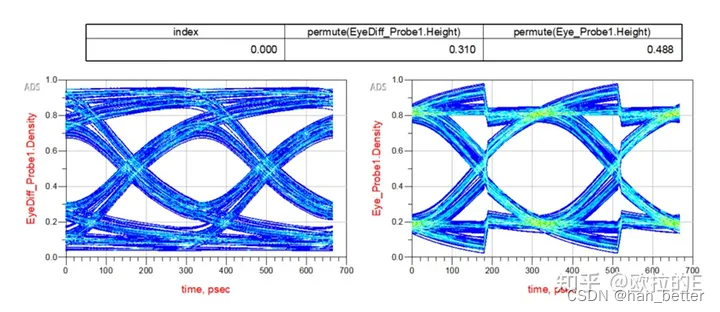
在如图 3 所示的通道仿真中， Rx_Diff 组件中对DFE 启用“优化的初始抽头计算”，如图 4 所示。当仿真结束时，最佳抽头值将被写入文本文件。 图 5 的左图显示了禁用 DFE 的眼图，图 5 的右图显示了启用 DFE 的眼图。 我们可以看到 DFE 改善了眼图。



DFE的功能本质上是降低了码间干扰，减少了每个信号的拖尾，使每1bit的信号响应都比较集中，进而增强了接收端信号的质量。

先前我们在讲 中提到了信道的时域响应存在拖尾现象，拖尾会影响到下一个码元，也就是常说的码间干扰(ISI)，当然信道的非理想还包含串扰，反射等现象。对于比较高的信道插损，线性均衡CTLE的效果存在上限，需要进一步的均衡机制。

图1

如图1，时域上，一种最直接原始的想法是，如果能够根据当前码元的判决结果，将该码元的后续影响依次全部消减，就可以把当前码元ISI的影响降到最低，甚至消除。这也是DFE作用最直观的描述。

基于上述思路，那么重点就是该如何实施和实现，如何做到对信道的自适应，系统的鲁棒性如何提高，算法如何设计的高效等一些列问题？本系列将试着研究回答这些问题。

图2

图2单脉冲冲激响应包含了3个后标（postcursor）量，1011的数据经过信道后的波形是对应脉冲移位叠加的结果。其中第二个数据0很容易出现误判。如果能够准确的判断第一个码元的话，将结果延迟反馈到输入信号处，并适当减掉部分量，则第二个码元0就更容易判断准确。这也是判决反馈均衡器(Decision-Feedback Equalier)的字面含义。

实现时，对于连续输入数据Din，通过时钟Clk控制的采样器Sampler，得到采样数据Dout，经过Td的延迟，通过权重h1和h2与输入数据相加。合适的延迟时间td和权重h1，h2就能保证将输入数据的码间干扰降低或完全消除，如图3。

图3

图3结构，需要考虑如下两个问题：

第一，Dout如果仅仅是采样输入数据Din，会存在量化精度的问题，比如用多少位表示。量化后的信号，需要决定反馈的权重h1和h2的大小及符号，对于NRZ编码的信号，采样后可用1bit的量化器量化为逻辑信号0和1。对于PAM4编码的信号，采用后通常会采用多bit的量化器(比如用ADC实现)。方便后续的数据处理。

图4

第二，延迟时间Td。如图4所示，全速率的RX结构，假如用上升沿采样数据，需要在一个采样时钟周期，也就是需要1个UI的时间内，将前一个UI的影响体现到后续的采样数据上。这里可以简单的理解Td<1UI。如果不满足，则无法体现消除效果。

注意NRZ编码的采样器量化后，转化为1bit逻辑，是非线性的转化过程。

实际电路实现时，采样器也叫Slicer，Slicer和延迟单元合并起来可以用DFF来表示。如图4所示，其中时序关键路径是图中黄色反馈路径，需要满足DFF的建立时间Tsetup，响应时间Tck-q，加法器响应时间Tsum三者之和小于1UI时间。

Tsetup+Tck-q+Tsum<1UI

图5

图5是最基本的DFE结构。其中Clk时钟频率和数据率相等(NRZ编码)。称之为全速率(Full-Rate)直接反馈(Direct Feedback)架构DFE。

图6给出了全速DFE对信号的均衡效果，Din经过1个Tap补偿后，输出波形Dout。可以看到对于高频数据，其判决幅度明显增大，更大概率判断处正确数据。

图6

Part2 DFE架构介绍

采样DFF的延迟时间Tck-q并没有明显减小，DFE反馈关键路径时序变得越来越难以满足。因此需要从结构上改进和优化这些问题。

随着数据速率的提高，图5的DFE有很多改进和优化结构。主要从这两方面分类。

首先是采样工作速率，分为全速率(Full-Rate)，半速率(Half-Rate)，1/4速率(Quarter-Rate)等等。

其次从时序关键路径，分为直接反馈(Direct Feedback)和开环(Loop Unrolled)结构。开环结构也称之为预判(Speculation)结构。预判式(Speculative)结构的Slicer个数会增加一倍。常见的是将h1这条关键路径进行开环，保证时序。在一些文献中，也见到过将前2个Tap全部使用预判结构，缺点是会使用比较多数量的Slicer。

图7是相对于图5结构对应的半速率实现形式，图中包含了h1和h2的时序路径中包含的各时间参数，以及需要满足的时序约束。注意半速率结构的采样时钟是数据率的一半，也就是使用的奈奎斯特频率时钟频率，奇(Odd)偶(Even)分别使用反相时钟clk和clkb进行交替采样。

图7

这里就要思考下采用半速率的得与失了。采用半速率，DFE部分的面积和功耗都会增加，那么优势是什么？其实从系统上看，功耗还是会减低的，主要是时钟产生电路PLL和时钟路径的功耗会有明显的减低。同时更低速时钟频率也能适当降低电路设计难度。

图8为全速率预判式DFE结构图，Tap1采用了预判结构，Tap2直接反馈。可以看到通过提前将h1和输入进行加减，并通过前一码元的结果对当前码元的结果进行选择。可以看到，这里边有3个加法器(Summer)，在实际电路实现时，通常将h1的summer和DFF合并，即为包含阈值的Slicer。

图8

图9和图10为半速率预判式DFE结构，通过将h1提前进行加减，可以节约Tap1路径的时间，增大时序裕量。

图9

图10

图11给了个典型的例子说明了不同结构的tap1和tap2的时间裕量。以及改进的半速率结构的优势。可以将缩减h2的时间，将h1的时间适当延长，拓展到2UI的时间。

图11

此外，还可以将Tap1和Tap2都提前与信号做加减，也就是2tap-Speculative结构的DFE，如图12。当该结构采用半速率，Data采样共需要8个Slicer。Tap1和Tap2系数C1和C2会提前按照符号和输入信号叠加，采样后利用前边2个码元进行Mux4to1的选择。

图12

实际实现的时候还有一些结构，会把其中的时间进行压缩，进一步提高速度，比如讲Summer和Slicer合并等，降低Summer的延时Tsum。

对于半速率预判式DFE，如果只有一个Tap，可以对奇偶数据进行多拍延迟，然后再做Mux选择。

在SerDes中，DFE通常还包含了其他采样器，用于实现DFE的自适应均衡，CDR锁定，LEQ的自适应，通路增益调节，数字眼图测量，Figure of Metric评估等功能，如图13所示。

图13

Part3 关键功能模块

在前两部分内容中，提到DFE结构中最常用的子模块包括采样器Slicer，加法器Summer，选择器Mux，延迟单元DFF&Latch等等，下边我们简单做下介绍。

• Slicer

采样器Slicer主要是用于对输入信号的量化，相当于1bit的ADC。量化后的逻辑可以看做恢复后的数据。其结构就是常规的灵敏放大器(Sense Amplifer,SA),或者称之为动态比较器(Dynamic Comparator)。

图14是一些常见的Slicer实现形式。其中(a)是基本类型，(b)是双尾电流(Double-Tail)动态比较器，©是改进型的双尾电流动态比较器。设计的重点是提升响应速度，提高输入灵敏度，降低功耗，减小回踢噪声，减小输入失调等。

图14

随着数据率的提高，如何降低动态比较器的输出响应时间，可能是优先级最高的考虑因素，只有保证数据正确，一切才有意义。输出响应时间和工艺制程，输入差分信号幅度，共模电平，电源电压都密切相关。其中先进工艺制程提供的更小的器件尺寸，为高速接口设计提供了最直接帮助。

需要注意到，图14中结构电路，在一个CLK周期的高低电平内，动态比较器需要完成预充电(Precharge)和放大(Amplification)的功能。因为时钟周期的一半是复位状态，因此需要剩余的半个时钟周期内完成采样量化，这里就解释了为什么半速率会比全速率结构能够留给动态比较器有更多的输出响应时间。也就更大概率分辨较小的输入信号，并得到正确数据。

动态比较器的输出只能保持少半个采样周期的输出数据，通常我们还需要另外的保持电路，"接棒"动态比较器输出，从而将采样结果保持一整个采样周期。

这也就是我们在图5到中提到的，用DFF的概念表示对数据采样和保持的功能。实际上我们用经常使用的概念Slicer，也可以泛指动态比较器和"接棒"的延迟单元。

• DFF & Latch

前边提到的Slicer中需要的延迟单元，可以是Latch，也可以是DFF。当然DFF可以看做是两个Latch结构的级联。

提到Latch，我们最先想到SR锁存器。可以由NAND2组成，也可以是NOR2组成的。基本的SR Latch不需要时钟，仅根据输入信号的变化，有不同的输出状态。如图15所示，两种结构的保持(Hold)状态的输入时不同的，可结合动态比较器的结构选择使用。

图15

基于选择器的锁存器(Multiplexer-Based Latch)由传输门选择器和反相器构成的，通过时钟进行控制。如图16所示，(a)和(b)分别是高电平锁存器和低电平锁存器。图中©是选择器和反相器的实现细节。

图16

将图16中的高低电平锁存器进行先后级联，可得到主从边沿触发触发器(Master-Slave Edge-Triggered Flip-Flop)。触发方式可以是上升沿，也可以是下降沿。其时序和结构如图17中(a)和(b)所示。

图17

除了上述的CMOS电平锁存器外，文献中常见的还有半电平的CML锁存器。

• Summer

加法器目的是完成输入Din和Tap量hn的加减操作。

图18所示CML结构电阻负载(Resistor Load)加法器，各Tap量通过电流相加，并通过电阻转化为电压信号供Slicer采样比较。电阻负载的结构存在输出摆幅，功耗，建立时间的考虑，其建立时间由输出节点的时间常数tau决定。例如3tau可以建立约95%的精度。主要影响了时序参数Tsum。

图18

图19是电流积分(Current Integrating)型加法器，通过时钟对负载电容CL进行复位和积分的分阶段重复操作。输出为归零(Return to Zero,RZ)信号。该结构比电阻负载加法器有着更高的能效，但文献中提到，该结构会存在3.9dB的直接积分损耗。

图19

图20是电荷舵(Charge Steering)型加法器。Razavi提到过该结构具有零静态功耗，同时动态功耗显著下降的新型加法器实现。复位阶段X和Y点被复位到电源，因此查分输出Vx-Vy实际上也可以看做RZ信号。

图20

需要注意，DFE补偿为了实现一定的精度，Tap量hn通常使用IDAC来实现，速度会比较快。不同tap的精度和范围会有差异。

• Mux

Mux本身的功能比较简单，目的就是将多路数(更多的是将2个路径数据)选择输出。可以直接用传输门结构，或者用具有3态控制的反相器实现即可，这里就不举例说明了。

• Merged Structure

除了以上基本的结构，在一些文献中还提到了混合型结构，从而可以进一步缩减tap反馈路径的时间。

图8中提到的带阈值的Slicer，就算作是混合结构。tap1权重h1的加法Summer和Sampler融合。结构如图21。通过DAC属猪的tap电压或者直接用逻辑控制输入对管M11和M21，实现对输入信号的Tap补偿。其中用逻辑直接控制的结构尤其适合低功耗场景下的1个Tap的预判式DFE设计，毕竟是牺牲了一定的速度和精度，才实现了低功耗的目的。

图21

前文提到的Slicer概念，其实也可以看做是Sampler和延迟单元Latch的合并的混合结构。

判决反馈均衡器DFE(中）

4. 瞬态波形和眼图

5. DFE对边沿的影响

6. 自适应算法简介

Part4 瞬态波形和眼图

判决反馈均衡器DFE(上）章节中提到的不同结构，其瞬态波形会存在差异。其采样前的眼图直观反映了采样器的幅度Margin和CDR采样时刻的裕度。

为了对比，这里使用VerilogA理想模型，激励条件尽可能保持了一致。模型数据率为10GT/s，输入信号为800mVppd。信道插入损耗约为10dB@5Ghz，无CTLE，仅DFE补偿，2个Tap。通过信道后，采样前数据眼图如图1所示。

图1

全速率直接反馈结构的瞬态相关波形和稳态眼图分别如图2和3。

图2

图3

收敛过程如动图4所示。可以比较明显观察到dfe补偿作用会导致采样时钟发生前移。

图4

半速率直接反馈结构的瞬态相关波形和稳态眼图分别如图5和6。图5可以看到加法器输入和加法器奇偶输出波形，通过interleave方式交替采样。

图5

图6

图7是奇偶路收敛过程的眼图。

图7

图8和图7一样，也是改进型半速率直接反馈结构的眼图，不知道大家能否看出差异?

图8

对于预判式全（半）速率结构其瞬态波形和眼图和上述两种直接反馈结构类似，只是tap1分量没有在summer节点上体现，需要根据判断出的数据选择对数据进行tap1量的加或者减。

Part5 DFE对边沿的影响

传统2x过采样CDR，通过edge定位锚定data采样位置，edge位置的抖动和分布实际上会影响到data采样的裕量，特别是在比较大插入损耗的情况下，眼睛裕量本身就比较小。

前边一系列动图可以明显看到dfe对采样时钟的相位影响，随着各tap补偿量的逐渐增加，采样时钟相位在cdr的调节下，相位逐步前移。cdr相位锁定位置的变化，反应了dfe对边沿的影响。

图9简单说明了DFE Tap1量的加减对边沿的影响，实际边沿数据变化和数据pattern，Tap阶数，响应时间密切相关。对于1-0的数据转换，pattern类型为110，可以看到Tap1量导致边沿提前；而pattern类型为010，因为存在tap1量符号反向，对边沿的影响和Tap量响应时间相关。

图9

实际上，对于多Tap的DFE补偿，边沿包含了历史多位数据的影响。综合影响评估需要结合具体电路实现。

其实，最明显的边沿影响，是预判式结构。因为Tap1量加减处理是在summer之后。如果不对edge采样进行处理，锁定后的数据采样位置就会偏后。如图10所示。

图10

那么该如何解决这个问题呢？这里就留给大家做个思考吧。

图11是对edge补偿处理后的结果，可以看到等效的眼图收敛结果更优。

图11

另外对2x过采样CDR时钟相位的影响。也需要考虑data和edge的先后顺序，和具体电路实现结构密切相关，具体哪种顺序更优，需要仔细评估。

这里总结下几种结构理想情况DFE收敛值情况，仅供参考。

图12

最后送上，用Matlab工具SerDes Toolbox计算的结果合成的封面图的近似收敛过程。

图13

Part6 自适应算法简介

目前，自适应滤波器理论已经非常成熟，在通信和消费领域也有着广泛的应用。例如信道均衡，波束成形，噪声消除等。如图14所示。

图14

自适应滤波器如图15，简单来讲，就是通过调整滤波器，使滤波器输出信号和目标信号接近或者相等。主要是(非)线性离散时间系统对离散信号的处理。通常使用性能函数(Performance Function)，评估不同滤波器系数的性能。比如用误差信号的均方误差(Mean-Squared Error,MSE)。最小均方误差的滤波器，又称之为维纳滤波器(Wiener Filter)。各种自适应算法就是要得到滤波器的维纳解(Wiener Solution)。

图15

在通信领域，自适应滤波器主要用作信道均衡(Channel Equalization)，如图16所示。图中信道H(z)是信道传递函数。噪声v(n)可以看做是串扰及噪声等非理想因素的组合。图中均衡器W(z)就是要消除码间干扰，降低串扰和噪声影响的自适应滤波器，均衡器输出y(n)需要满足量化输出的数据在规定的误码率范围内。

图16

图17是维纳滤波器的数学推导1，滤波器系数满足维纳-霍普方程，维纳解形式包含输入数据自相关矩阵R，输入数据和目标数据的互相关向量p的关系。可以看到维纳解是可以一步到位，但会涉及比较复杂的矩阵运算量。

图17

另一种方法通过迭代搜索算法，从任意一个Tap权重向量wi，逐步迭代收敛到最优权重向量wo。这里就要提到基于梯度的最速下降法(method of steepest descent)。图18[2]给出个动画，还是比较形象的说明了梯度下降法，整个性能误差面一定会存在最低点(可能包含多个局部最低点)，这个点也就是维纳解的位置。

图18

基于梯度的最速下降示意图及推导过程如图19所示。可以看到基于梯度的最速下降法能够以最快的方式按照负梯度方向，朝着维纳解位置运动。同时，迭代步长增益μ和自相关矩阵R的特征根λi需要满足一定的关系从而保证收敛过程的稳定性。

图19

图19中基于梯度的最速下降法还是需要知道自相关矩阵R和互相关矩阵p。计算过程还是比较复杂。我们知道前述梯度是误差平方期望的梯度，如果我们用瞬时误差梯度代替期望误差梯度，则可以简化迭代过程为LMS算法实现，如图20所示。

图20

图20的LMS迭代过程使用了瞬时误差e(n)和历史数据矩阵x(n)。还是会涉及到浮点运算（乘法和加法）。运算硬件消耗也是比较大。于是就有了图21所示的简化版本。主要是误差或者历史数据的符号化。可以不同程度简化计算复杂度。不过图中也可以简化计算的代价是收敛时间，还有可能残余更大的均方误差MSE。

图21

判决反馈均衡器(Decision Feedback Equalizer,DFE)，正如其名字所示，需要通过历史判决值，构成反馈FIR滤波器，对输入信号进行补偿。如图22所示。需要注意的是，图中Tap反馈到加法器为负，也就是实现减法。同时误差信号的定义和前述基本滤波器定义也是相反的。负负为正。因此权重迭代表达式符号也和前述结果相同。

图22

图22中当采样器量化精度为1bits时，就实现图21中sign-sign LMS，实际电路实现时，通过分时复用和模版数据选择，可以进一步降低硬件实现成本。

当滤波器收敛后，tap系数趋于稳定。滤波器输出值和输入数据及量化误差的传递函数如图23所示。

图23

图24是简单的一阶DFE传递函数及零极点分布，可以看到信号传递函数是高通(高阶DFE频响特性不一定具有全频段的高通特性)，衰减低频，提升高频。从而补偿输入数据的拖尾。误差传递函数整体增益是衰减的。

图24

DFE总结下来有如下的特点：

1.具有衰减低频，补偿高频的特性，但不会放大噪声和串扰。

2.符号化的量化具有非线性特性。

3.DFE无法消除前标，只能消除后标。

4.DFE存在错误传递的可能性。

5.DFE在消除ISI的同时增加了CDR相位检测的复杂性。

判决反馈均衡器DFE(下）

7. VerilogA模型

8. 模型结果说明

9. PAM4下的DFE

7.VerilogA模型

Verilog-A Hardware Description Language(HDL)是IEEE定义的用于描述模拟系统(Analog Systems)行为的硬件描述语言。通过对子模块建模，可实现项目初期系统级模型搭建和仿真验证。提供研究阶段的可行性分析。自顶向下(TOP-DOWN)设计流程，方便从系统角度，明确定义关键子模块参数和指标要求。

如图1，Verilog-A是Verilog-AMS的一个纯模拟子集(Analog-Only Subset)，结合verilog或者VHDL可实现数模混合信号的系统验证。目前主流仿真器工具spectre，spice，ADS等都支持Verilog-A语言。

图1

相对于Verilog/VHDL语言，模拟设计人员更熟悉Verilog-A，也表现的更友好。常见模块如运放，比较器，AD/DA，PLL等。可以很方便的实现理想替代，方便及加速模拟设计验证。

在前文中我们对SerDes Rx部分进行纯Verilog-A的建模，并重点分析了DFE这个小系统。

实际上，像CTLE，DFE，CDR，DESER等可以建模实现，同样可以构成TX和PLL，并最终形成具有层级（hierarchy）关系的大系统。

通常EDA工具都会提供 Verilog-A帮助文档，详细语法解释和实用例子都能帮助新手比较快的入门。图2简单列举了下Verilog-A中常见的功能函数。

图2

针对具体的建模需求，Reference文档外加互联网资源都可作为参考，多练多用，相信很快就能构建模块基本功能的建模需求。更复杂的功能就需要深度理解电路非理想特性，定制高阶功能性能了。图3的教材提供了AMS系统设计及仿真的说明，有兴趣的可以参考下。

图3

8.模型结果说明

这里着重介绍下DFE相关的模型，涉及到模拟部分的Verilog-A建模和算法的Verilog或者Verilog-A实现。

图4列出了DFE模拟模块，包含加法器，动态比较器，乘法器，延迟单元，多路选择器，数据对齐（Align）及DFE算法VA模型。

图4

算法的实现可以数字HDL语言的方式通过Verilog或者VHDL实现，最后使用混合仿真的方式来验证。当然在初期模型阶段，使用VerilogA实现的算法模型可以通过浮点型数据实现更接近基本原理的算法Demo。规模也更小，验证速度也会更快。

通过图4的基本模型单元，就可以搭建前边DFE系列文章中提到的不同架构，对比评估架构差异和性能表现。图5所示是其中的一个DFE评估的子系统。

图5

图4-5中DFE的子模块功能只包含了基本功能，当然也可能实现更复杂的功能。比如加法器建立时间、tap分辨率，动态比较器的输入失调、噪声及延迟时间。收敛算法的更新速率、精度等。

模型的复杂度和仿真速度是正相关的。这个就需要根据建模验证的目的选择合适的模型精度。

最后，要注意的是，接收机部分包含了LEQ均衡及算法、CDR的环路，DFE补偿及算法，多环路多种算法之间耦合，造成相互影响，所有的小系统功能点评估最后都需要在整体系统整体上做性能回归，保证小系统评估的准确性。

9.PAM4下的DFE

随着SerDes线速率按照几乎翻倍的形式提升，信号带宽的变化面临着信道插损越来越高的难题，也对均衡能力提出了更高的挑战。

目前看来，更高阶的编码方式，从NRZ(或者PAM2)转变到PAM4，是一种比较有效的解决方案。从而维持奈奎斯特频率不变的基础上加倍数据率。PAM4的编码相对于NRZ的变化如图6所示。

图6

PAM4相对NRZ编码信号幅度下降到1/3，SNR 下降了9.5dB，绝对眼宽也会减小。这些对接受侧的实现会有更高的要求，但总体上，牺牲信噪比换来的带宽保持不变还是有收益的。

图7

目前从主流协议标准来看，如图8是光互联论坛OIF针对56/112G定义的不同互联场景，信道距离SR-MR-LR及信号编码等都差异化定义，针对不同场景，可以对接收侧的架构实际上差异化设计。

图8

目前PAM4编码的接收侧架构，针对SR低插损场景，主要是基于传统NRZ升级结构的实现形式，如图9[1]和图10[2]所示。包含多电平量化，PAM4编解码，CDR 鉴相pattern变化等新增功能点。

图9

插损较小的XSR/VSR场景，甚至都不需要纠错机制就能保证比较低的误码率，就能实现高效能的数据传输。

图10

针对MR-LR信道高插损场景，图11是基于ADC采样结构的SerDes RX结构[3],接收端AFE包含CTLE+VGA的均衡，经过6-8bits精度的TI-ADC采样量化，在数字域使用DSP实现FFE+DFE的组合均衡。

这种ADC+DSP的实现形式，因为其后续强大的数字均衡能力，具有很高的潜力。在超高速的中长距应用中越来越广泛。

图11

图12是文献[4]提供的DSP实现框图，包含多阶FFE+1Tap DFE的。数字域实现的均衡算法收益很多，因为算法实现对工艺相对不敏感，可充分利用先进工艺的特点，能够实现高速低功耗，小面积目标，数字实现也更加灵活，工艺演进中迁移更容易。当然也就更考验算法调教，算法鲁棒性等。

图12

最后，送上一个用excel模拟离散时间域DFE算法的简单Demo，如图13-15。采用全速率直接反馈结构，Vref和Tap自适应，Tap收敛使用的仍然是前文介绍的SS-LMS算法。

图13

图13所示，脉冲响应主标H0(Main Cursor)是0.6，后标H1-H3分别为0.2、0.15和0.05。Vref/Tap更新步长也存在差异，3个DFE Tap补偿全部开启。

图14

图14是Vref和3个Tap的收敛过程。可以看到收敛完成结束时，后标H1-H3都几乎完美地被消除掉。

图15是采样点收敛过程散点图，眼高可以从0.4Vppd增加到1.2Vppd。

图15

关于DFE的这个系列内容就这么多了，希望大家能够有所收获。