B树是什么？

B树是一种多路平衡查找树

平衡，指的是子树高度相同（即所有叶子结点均在同一层），即每个结点的平衡因子均等于0

多路，就是它除了根结点外（之所以根结点的分叉数不限定，是因为当整棵树只有1个关键字，根结点只能有2个分叉），其余每个结点都至少有m/2向上取整 个分叉。（m是它的阶，同时m也是结点的最大分叉数，也可以理解为每个结点最多有m棵子树）

（1）所有结点中，拥有孩子个数最多的，也就是分叉数最大值，称为整棵B树的阶。
例如：结点最多有3个分叉，则称为3阶B树
（2）每个结点中包含的多个数据元素，称之为“关键字”，当某个结点有m棵子树的时候，则一定有m-1个关键字。
如下图中有3个分叉的结点，只能在缝隙中塞3-1=2个关键字

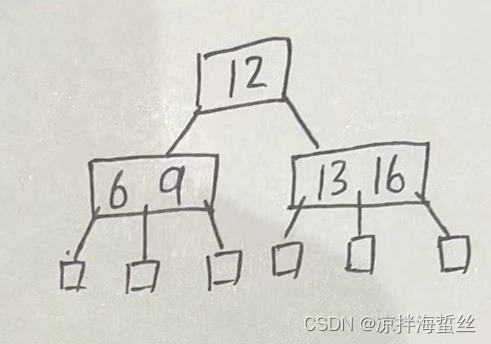
（3）若根结点不是终端结点（终端结点是叶子结点的再上一层结点，这里的叶子结点其实是不存在的，是代表查找失败的结点，不携带任何关键字信息，终端结点才是真实有关键字存放的“叶子结点”，但是它又称为终端结点），则它最少都有2棵子树（也就是最少都有一个关键字才能占一个结点，一个关键字左右又可以产生分叉，所以最少都有两棵子树）
（4）跟二叉排序树有点类似，B树也遵循左小右大原则，但是由于它一个结点里会有多个关键字，所以它也有多个范围。如下图：

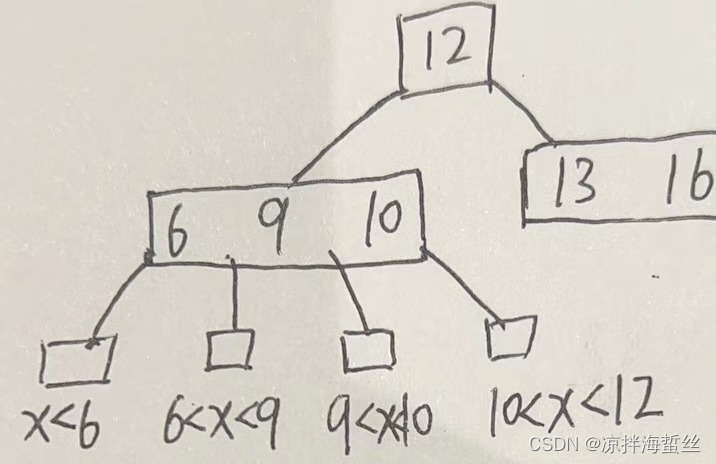
B树的查找过程：

假设X=8
1:根据查找目标X从根结点12开始比较，比12小，往左子树，比12大，往右子树
2:到了左子树的根结点，顺序依次比较（也可以采用二分查找的方法）6，9，10；发现9<X<10；于是顺着这个分叉指针往下，但是发现为null，即不存在这个范围。这时候就知道B树中不包含对应关键字，返回查找失败。

（5）结点内的数据从左到右递增有序。

（6）除根结点外，所有非叶子结点至少有m/2（向上取整） 个分叉（棵子树），即至少含有 m/2（向上取整） -1 个关键字。
为什么非叶子结点至少有 m/2 （向上取整）个分叉（棵子树）呢？

B树的生成和插入：

假设某棵B树的阶设为m=5, 即每个结点至多有4个关键字，在插入关键字的时候，会首先通过上述的B树查找方式，定位新关键字应该存放在哪个位置，然后把关键字塞进去，但是这会有一个问题，假如对应的终端结点已经有4个关键字了，又要塞进来一个，导致不满足5阶B树的性质，就会引起“分裂”。（即当插入新的关键字后，对应终端结点的关键字数小于等于m-1，则插入成功，当某结点关键字数会大于m-1时，该结点就必须分裂），如下图所示：

所以，每个结点都是被分裂出来的，而发生分裂的时候，就保证了该结点一定是满了要溢出来了，分裂后的每个结点都一定一定会有m/2(向上取整)-1个关键字（根结点除外），那么肯定会有 m/2 （向上取整）个分叉（棵子树）。
⚠️：并不是每次分裂，树都会长高一层，必须是分裂引起了根结点的分裂，树才会长高一层，如果没影响到根结点分裂，那么不管怎么分裂，树都不会长高。

（7）B树中的结点中都包含了关键字对应记录的真实存储地址（一般B树中关键字都是ID，UserId之类的东西）。所以在查找中，某一层匹配了目标关键字，则马上拿着关键字的存储地址去磁盘中找。

（8）既然插入是新增，那么删除肯定对应着合并操作。但是删除后还要维持着B树的特性，所以要看针对删除的关键字的位置进行处理

B树的删除：

还是以上面的5阶B树为例，设要删除的关键字是X
类型1:X处于终端结点，且（删除前的）终端结点的关键字个数>= m/2（向上取整），则直接删除。

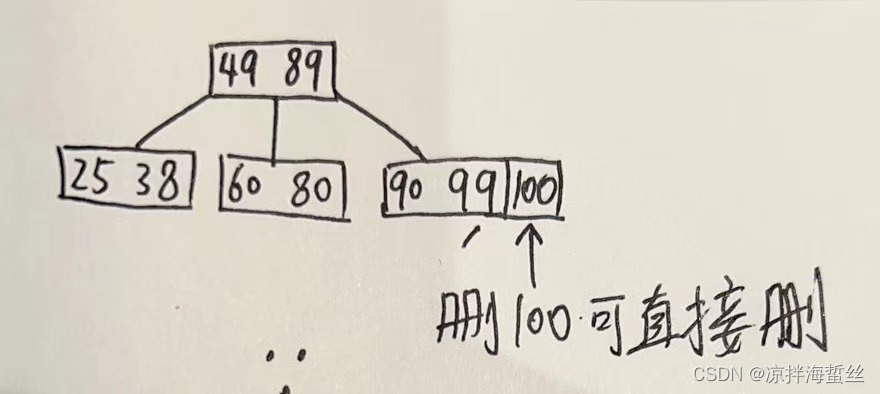
类型2:X处于终端结点，但终端结点的关键字个数刚好是= m/2（向上取整），删掉一个后不满足B树定义，这个时候就要考虑如何补上这个空缺。又分为父子换位大法和拉爹下水大法

父子换位大法：当某个结点删除后关键字不够支撑这棵树的定义，看看该结点左右兄弟有没有多余的可以借用的结点，如果有，就把借用的那个兄弟的关键字抬上去父结点，把父结点对应的关键字填补回不满足定义的那个结点。

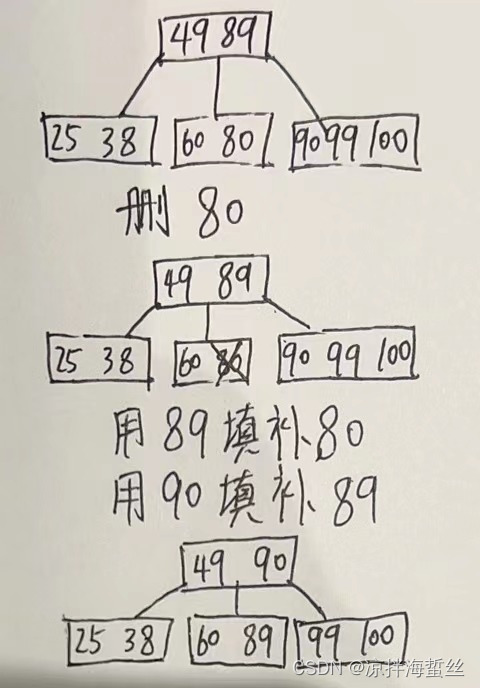
拉爹下水大法：当左右兄弟家的关键字数也是勉强够自己支撑，匀不出来，这个时候只能拉爹下水，一起支撑这棵树

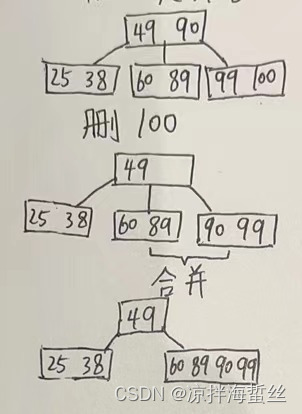
类型3:X处于非终端结点，则用X的前驱或者后继关键字顶替X的位置，然后把对应的前驱和后继关键字删掉，变成删除终端结点的情况。

优缺点

优：在查询中，外存也就是磁盘IO是最低效率的，而树的结构在数据量比较大的时候，一般都选择链式存储，链式存储就会使得数据分散在磁盘的各个角落，要不停进行寻道读取的磁盘IO，而使用B树，由于每一个结点放多个关键字数据，很大程度上压缩了树的深度，每一个结点采用连续存储的数组形式，读入内存后查询速度大大提升，同时能够减少IO次数，进而提升查询速度。
缺：部分关键字在非终端结点中，部分关键字在终端结点，所以没办法进行范围查询，同时又因为每个结点包含了关键字的存储信息，占用了一部分的空间，注定会影响每个结点的的关键字个数，进而没有把磁盘IO优化到最优。

B+树

B+树是B树的变形，而且它是数据库底层很重要的一种数据结构。
（1）非叶子结点不包含关键字的存储地址。
（2）一个关键字对应一棵子树，即一个关键字屁股后面连着一个分叉。所以n个关键字的结点包含n棵子树。

B树中的分叉是夹在关键字中间的，这是判断题目中的树是B还是B+最突出的区别，看分叉的位置

（3）⚠️根结点至少要有两棵子树（两个分叉），分支结点至少要有 m/2（向上取整）棵子树。

B树允许根结点仅有1个关键字，B+树要有2个

（4）所有关键字（包括出现在非叶子结点上的），都会出现在叶子结点中，并且叶子结点中按照关键字大小排序，且用链表形式把相邻的叶子结点互相连接。因此B+树支持顺序范围查找。同时B+Tree有两个头指针，一个是指向根结点，另外一个指向最小关键字的叶子结点。

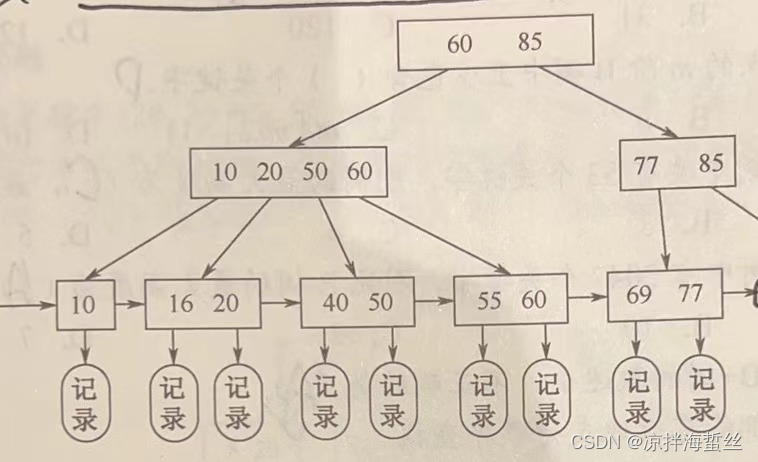
（5）由于B+树的记录全部在叶子结点中才能找到，所以在搜索时候一定会找到最底层，而B树在中间结点找到目标关键字后就会返回。
（6）由于B+树非叶子结点都不含有关键字对应记录的存储信息，所以可以使一个连续的磁盘空间存储更多的关键字，从而使得阶数更大，树更矮，进一步减少磁盘IO次数。