目录
1 概念
2 权值初始化方法
2.1 常数初始化
2.2 均匀分布初始化
2.3 正态分布初始化
2.4 Xavier 均匀分布
2.5 Xavier 正态分布
2.6 kaiming 均匀分布
2.7 kaiming 正态分布
2.8 单位矩阵初始化
2.9 正交初始化
2.10 稀疏初始化
2.11 狄拉克δ函数初始化
3 python示例
1 概念
权值初始化是指在网络模型训练之前,对各节点的权值和偏置初始化的过程,正确的初始化会加快模型的收敛,从而加快模型的训练速度,而不恰当的初始化可能会导致梯度消失或梯度爆炸,最终导致模型无法训练。
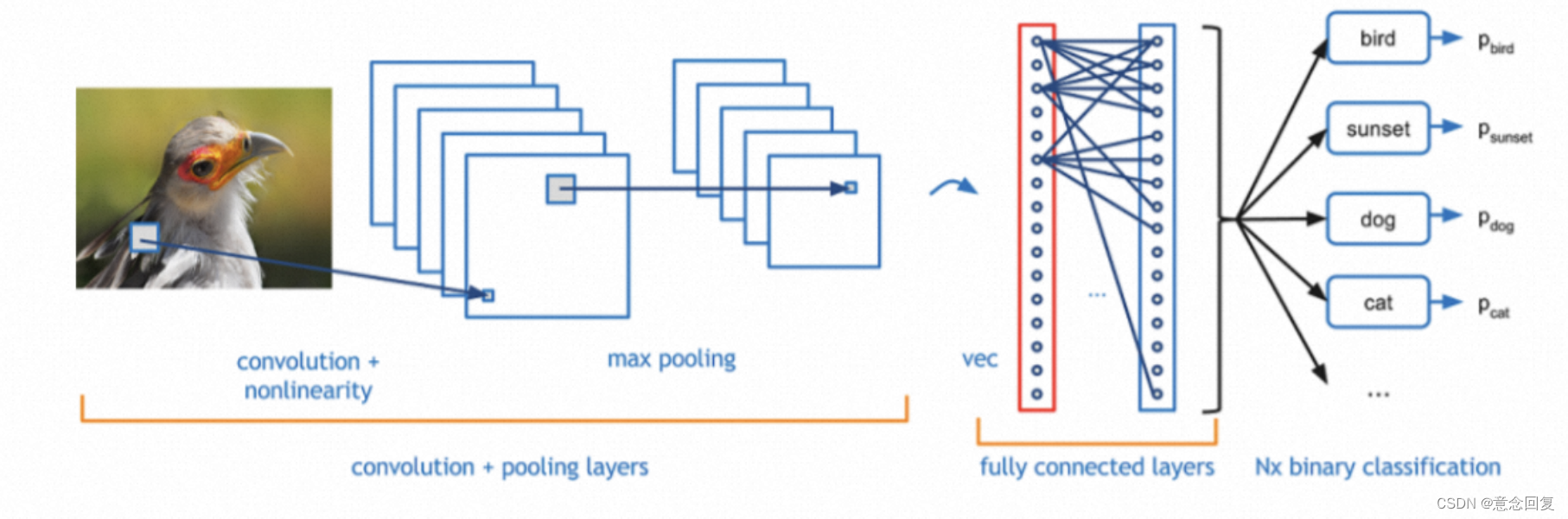
如上图所示的一个基本的CNN网络结构,数据在网络结构中流动时,会有如下的公式(默认没有偏置):
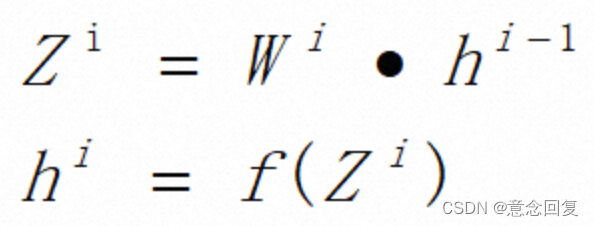
在反向传播的过程中,由于是复合函数的求导,根据链式求导法则,会有两组导数,一个是损失函数Cost对Z的导数,一个是损失函数对W的导数,
1、损失函数关于状态Z的梯度:

2、损失函数关于W的梯度:

可以看出,在网络结构中,一个参数的初始化关系到网络能否训练出好的结果或者以多快的速度收敛。所以对权值初始化有如下的要求:
- 参数不能全部初始化为0或全为1,也不能全部初始化同一个值;(反向传播时梯度的更新值一样)
- 参数的初始化值不能太大;(针对激活函数是sigmoid和tanh,参数太大,梯度会消失)
- 参数的初始化值也不能太小;(针对激活函数是relu和sigmoid,参数太小,梯度会消失)
一、所有的参数初始化为0或者相同的数
最简单的初始化方法是将所有的参数初始化为0或者一个常数,但是使用这种特征会使网络中的所有神经元学习到的是相同的特征。
假设神经网络中只有一个有2个神经元的隐藏层,现在将偏置参数初始化为:bias=0,权值矩阵初始化为一个常数α。 网络的输入为(x1,x2),隐藏层使用的激活函数为ReLU,则隐藏层的每个神经元的输出都是relu(αx1+αx2)。 这就导致,对于loss function的值来说,两个神经元的影响是一样的,在反向传播的过程中对应参数的梯度值也是一样,也就说在训练的过程中,两个神经元的参数一直保持一致,其学习到的特征也就一样,相当于整个网络只有一个神经元。
二、过大或过小的初始化
如果权值的初始值过大,则会导致梯度爆炸,使得网络不收敛;过小的权值初始值,则会导致梯度消失,会导致网络收敛缓慢或者收敛到局部极小值。如果权值的初始值过大,则loss function相对于权值参数的梯度值很大,每次利用梯度下降更新参数时,参数更新的幅度也会很大,这就导致loss function的值在其最小值附近震荡。而过小的初始值则相反,loss关于权值参数的梯度很小,每次更新参数时,更新的幅度也很小,着就会导致loss的收敛很缓慢,或者在收敛到最小值前在某个局部的极小值收敛了。
2 权值初始化方法

2.1 常数初始化
用val的值填充输入的张量或变量
torch.nn.init.constant_(tensor, val)
参数:
tensor – n维的torch.Tensor或autograd.Variable
val – 用来填充张量的值
使用:
w = torch.empty(3, 5)
nn.init.constant_(w, 0.3)
2.2 均匀分布初始化
从均匀分布U(a, b)中生成值,填充输入的张量或变量
torch.nn.init.uniform_(tensor, a=0, b=1)
参数:
tensor - n维的torch.Tensor
a - 均匀分布的下界
b - 均匀分布的上界
2.3 正态分布初始化
从给定均值和标准差的正态分布N(mean, std)中生成值,填充输入的张量或变量
torch.nn.init.normal_(tensor, mean=0, std=1)
参数:
tensor – n维的torch.Tensor
mean – 正态分布的均值
std – 正态分布的标准差
2.4 Xavier 均匀分布
用一个均匀分布生成值,填充输入的张量或变量。结果张量中的值采样自U(-a, a),其中a= gain * sqrt( 2/(fan_in + fan_out))* sqrt(3). 该方法也被称为Glorot initialisation
torch.nn.init.xavier_uniform_(tensor, gain=1)
参数:
tensor – n维的torch.Tensor
gain - 可选的缩放因子
2.5 Xavier 正态分布
用一个正态分布生成值,填充输入的张量或变量。结果张量中的值采样自均值为0,标准差为gain * sqrt(2/(fan_in + fan_out))的正态分布。也被称为Glorot initialisation.
torch.nn.init.xavier_normal_(tensor, gain=1)
参数:
tensor – n维的torch.Tensor
gain - 可选的缩放因子
2.6 kaiming 均匀分布
用一个均匀分布生成值,填充输入的张量或变量。结果张量中的值采样自U(-bound, bound),其中
torch.nn.init.kaiming_uniform_(tensor, a=0, mode='fan_in', nonlinearity='leaky_relu')
参数:
tensor – n维的torch.Tensor
a -这层之后使用的rectifier的负斜率系数(ReLU的默认值为0)
mode - fan_in 保留前向传播时权值方差的大小,fan_out 保留反向传播时的大小。默认:fan_in
nonlinearity –非线性函数,推荐使用relu和leaky_relu,默认leaky_relu
2.7 kaiming 正态分布
用一个正态分布生成值,填充输入的张量或变量。结果张量中的值采样自的正态分布。
torch.nn.init.kaiming_normal_(tensor, a=0, mode='fan_in', nonlinearity='leaky_relu')
参数:
tensor – n维的torch.Tensor
a -这层之后使用的rectifier的负斜率系数(ReLU的默认值为0)
mode - fan_in 保留前向传播时权值方差的大小,fan_out 保留反向传播时的大小。默认:fan_in
nonlinearity –非线性函数,推荐使用relu和leaky_relu,默认leaky_relu
2.8 单位矩阵初始化
用单位矩阵来填充2维输入张量或变量。在线性层尽可能多的保存输入特性。
torch.nn.init.eye_(tensor)
参数:
tensor – 2维的torch.Tensor
2.9 正交初始化
用(半)正交矩阵填充输入的张量或变量。
torch.nn.init.orthogonal_(tensor, gain=1)
参数:
tensor – n维的torch.Tensor或 autograd.Variable,其中n>=2
gain -可选
2.10 稀疏初始化
将2维的输入张量或变量当做稀疏矩阵填充,其中非零元素根据一个均值为0,标准差为std的正态分布生成。
torch.nn.init.sparse_(tensor, sparsity, std=0.01)
参数:
tensor – n维的torch.Tensor或autograd.Variable
sparsity - 每列中需要被设置成零的元素比例
std - 用于生成非零值的正态分布的标准差
2.11 狄拉克δ函数初始化
使用狄拉克δ函数填充输入的torch.Tensor。
torch.nn.init.dirac_(tensor)
参数:
tensor – {3, 4, 5}维的torch.Tensor
3 python示例
import torch.nn as nn
import torch
class Net(nn.Module):
def __init__(self):
super().__init__()
self.conv1 = nn.Conv2d(3, 3, (3, 3), stride=(1, 1), padding=1)
self.bn1 = nn.BatchNorm2d(3)
self.relu = nn.ReLU()
def forward(self, x):
x = self.relu(self.bn1(self.conv1(x)))
return x
# init.uniform a, b均值分布的上下限
class model_param_init(nn.Module):
def __init__(self, model):
super().__init__()
assert isinstance(model, nn.Module), 'model not a class nn.Module'
self.net = model
self.initParam()
def initParam(self):
for param in self.net.parameters():
# nn.init.zeros_(param)
# nn.init.ones_(param)
# nn.init.normal_(param, mean=0, std=1)
# nn.init.uniform_(param, a=0, b=1)
# nn.init.constant_(param, val=1) # 将所有权重初始化为1
# nn.init.eye_(param) # 只能将二维的tensor初始化为单位矩阵
# nn.init.xavier_uniform_(param, gain=1) # Glorot初始化 得到的张量是从-a——a中采用的
# nn.init.xavier_normal_(param, gain=1) # 得到的张量是从0-std采样的
nn.init.kaiming_normal_(param, a=0, mode='fan_in', nonlinearity='leaky_relu') # he初始化方法
# nn.init.kaiming_uniform_(param)
if __name__ == '__main__':
net = Net()
net = model_param_init(net)
for param in net.parameters():
print(param)
# 按照参数更改权重
for name, param in net.named_parameters():
if name == net.conv1.weight: # 指定更改某层的权重值
nn.init.dirac_(param, groups=1) # 保留卷积层通道的值
print(param)
PyTorch学习之十一种权重初始化方法_51CTO博客_pytorch权重初始化
Pytroch进行模型权重初始化_pytorch权重初始化_像风一样自由的小周的博客-CSDN博客
pytorch学习笔记九:权值初始化_Dear_林的博客-CSDN博客