树

树（Tree）是n（n≥0）个节点的有限集合T，它满足两个条件 ：

有且仅有一个特定的称为根（Root）的节点；

其余的节点可以分为m（m≥0）个互不相交的有限集合T1、T2、……、Tm，其中每一个集合又是

一棵树，并称为其根的子树 表示方法 ：树形表示法、目录表示法。

一个节点的子树的个数称为该节点的度数

一棵树的度数是指该树中节点的最大度数。

度数为零的节点称为树叶或终端节点

度数不为零的节点称为分支节点 除根节点外的分支节点称为内部节点。

 

一个节点系列k1,k2, ……,ki,ki+1, ……,kj,并满足ki是ki+1的父节点，就称为一条从k1到kj的路径

路径的长度为j-1,即路径中的边数。

路径中前面的节点是后面节点的祖先，后面节点是前面节点的子孙。

节点的层数等于父节点的层数加一，根节点的层数定义为一。

树中节点层数的最大值称为该树的高度或深度。

 

若树中每个节点的各个子树的排列为从左到右，不能交换，即兄弟之间是有序的，则该树称为有序树。

m（m≥0）棵互不相交的树的集合称为森林。

树去掉根节点就成为森林，森林加上一个新的根节点就成为树。

树的逻辑结构 ：树中任何节点都可以有零个或多个直接后继节点（子节点），但至多只有一个直

接前趋节点（父节点），根节点没有前趋节点，叶节点没有后继节点。

二叉树

  二叉树是n（n≥0）个节点的有限集合

或者是空集（n＝0）

或者是由一个根节点以及两棵互不相交的、分别称为左子树和右子树的二叉树组成

严格区分左孩子和右孩子，即使只有一个子节点也要区分左右。

二叉树的性质

二叉树第i（i≥1）层上的节点最多为2i-1个。

深度为k（k≥1）的二叉树最多有2k－1个节点。

满二叉树 ：

深度为k（k≥1）时有2k－1个节点的二叉树。

完全二叉树 ：

只有最下面两层有度数小于2的节点，且最下面一层的叶节点集中在最左边的若干位置上。

具有n个节点的完全二叉树的深度为          （log2n）＋1或『log2(n+1)。

顺序存储结构 ：

完全二叉树节点的编号方法是从上到下，从左到右，根节点为1号节点。设完全二叉树的节点数为n，某节点编号为i

当i＞1（不是根节点）时，有父节点，其编号为i/2;

当2*i≤n时，有左孩子，其编号为2*i ,否则没有左孩子，本身是叶节点;

当2*i＋1≤n时，有右孩子，其编号为2*i+1 ,否则没有右孩子；

当i为奇数且不为1时，有左兄弟，其编号为i-1,否则没有左兄弟；

当i为偶数且小于n时，有右兄弟，其编号为i＋1,否则没有右兄弟；

 有n个节点的完全二叉树可以用有n+1个元素的数组进行顺序存储，

节点号和数组下标一一对应，下标为零的元素不用。

利用以上特性，可以从下标获得节点的逻辑关系。

不完全二叉树通过添加虚节点构成完全二叉树，然后用数组存储，这要浪费一些存储空间。

二叉树链式存储

typedef  int  data_t ;

typedef  struct  node_t;

         {

    data_t data ;

    struct node_t *lchild ,*rchild ;

     } bitree_t ;

     bitree_t *root ;      二叉树由根节点指针决定。

 

二叉树的运算

遍历 ：沿某条搜索路径周游二叉树，对树中的每一个节点访问一次且仅访问一次。

二叉树是非线性结构，每个结点有两个后继，则存在如何遍历即按什么样的搜索路径进行遍历的问题。

二叉树的遍历

由于二叉树的递归性质，遍历算法也是递归的。三种基本的遍历算法如下 ：

先访问树根，再访问左子树，最后访问右子树；

先访问左子树，再访问树根，最后访问右子树；

先访问左子树，再访问右子树，最后访问树根；

先序遍历算法

若二叉树为空树，则空操作；否则

访问根结点

先序遍历左子树

先序遍历右子树

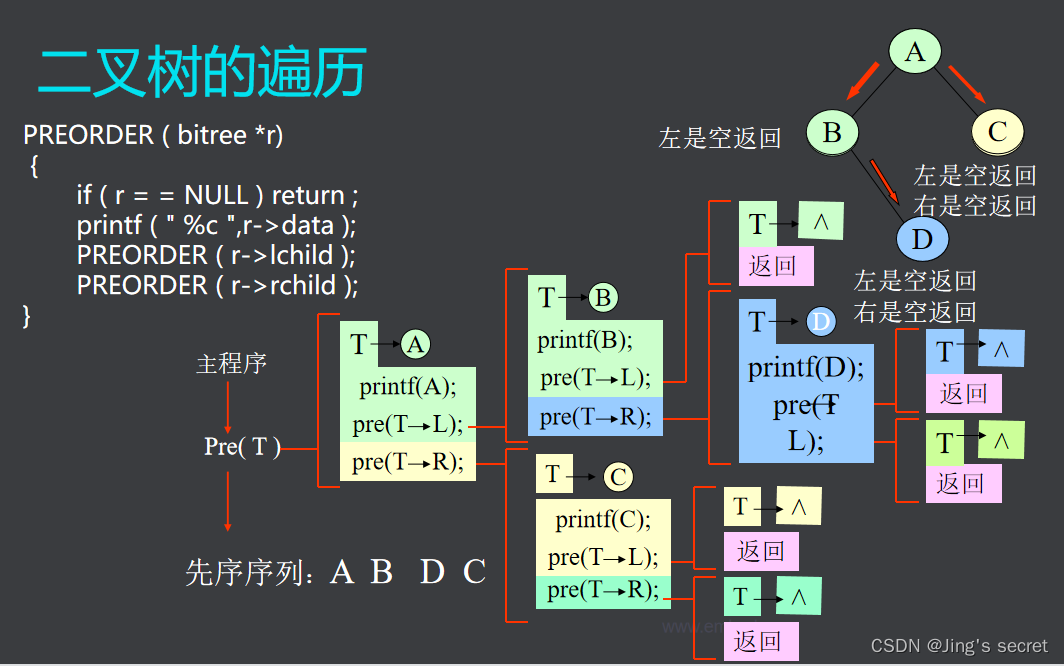
先序遍历算法

void  PREORDER ( bitree *r) {

    if ( r = = NULL ) return ;     //空树返回

    printf ( “ %c ”,r->data );       //先访问当前结点

    PREORDER( r->lchild );     //再访问该结点的左子树

    PREORDER( r->rchild );     //最后访问该结点右子树

}

 

中序遍历算法

若二叉树为空树，则空操作；否则

中序遍历左子树

访问根结点

中序遍历右子树

    中序遍历算法

void  INORDER ( bitree *r) {

    if ( r = = NULL ) return ;   //空树返回

    INORDER( r->lchild );     //先访问该结点的左子树

    printf ( “ %c ”,r->data );    //再访问当前结点

    INORDER( r->rchild );     //最后访问该结点右子树

}

后序遍历算法

若二叉树为空树，则空操作；否则

后序遍历左子树

后序遍历右子树

访问根结点

     后序遍历算法

void  POSTORDER ( bitree *r) {

    if ( r = = NULL ) return ;     //空树返回

    POSTORDER( r->lchild );   //先访问该结点的左子树

    POSTORDER( r->rchild );  //再访问该结点右子树

    printf ( “ %c ”,r->data );       //最后访问当前结点

}

二叉树的遍历

遍历的路径相同，均为从根节点出发，逆时针沿二叉树的外缘移动，每个节点均经过三次。按不同的次序访问可得不同的访问系列，每个节点有它的逻辑前趋（父节点）和逻辑后继（子节点），也有它的遍历前趋和遍历后继（要指明遍历方式）。

按编号遍历算法 ：

    NOORDER  ( bitree *r)         /*按编号顺序遍历算法*/

{

           int  front,  rear;

           bitree  *Q[N];

if ( r == NULL ) return ;         /*空树返回*/

for (rear=1;rear<N; rear++) Q[rear] = NULL ;

front = rear = 1;  Q[rear] = r;

while ( Q[front] != NULL ) {    /*以下部分算法由学生完成设计*/

         /*访问当前出队节点*/

         /*若左孩子存在则左孩子入队*/

         /*若有孩子存在则右孩子入队*/

         /* front向后移动*/

}  }