前言：

算法训练系列是做《代码随想录》一刷，个人的学习笔记和详细的解题思路，总共会有60篇博客来记录，计划用60天的时间刷完。

内容包括了面试常见的10类题目，分别是：数组，链表，哈希表，字符串，栈与队列，二叉树，回溯算法，贪心算法，动态规划，单调栈。

博客记录结构上分为思路，代码实现，复杂度分析，思考和收获，四个方面。

如果这个系列的博客可以帮助到读者，就是我最大的开心啦，一起LeetCode一起进步呀；）

LeetCode435. 无重叠区间

1. 思路

2. 代码实现

3. 复杂度分析

4. 思考与收获

LeetCode763. 划分字母区间

1. 思路

2. 代码实现

3. 复杂度分析

4. 思考与收获

Leetcode 56. 合并区间

1. 思路

2. 代码实现

3. 复杂度分析

4. 思考与收获

LeetCode435. 无重叠区间

链接：435. 无重叠区间 - 力扣（LeetCode）

1. 思路

**相信很多同学看到这道题目都冥冥之中感觉要排序，但是究竟是按照右边界排序，还是按照左边界排序呢？**这其实是一个难点！

排序和遍历顺序？

按照右边界排序，就要从左向右遍历，因为右边界越小越好，只要右边界越小，留给下一个区间的空间就越大，所以从左向右遍历，优先选右边界小的；
按照左边界排序，就要从右向左遍历，因为左边界数值越大越好（越靠右），这样就给前一个区间的空间就越大，所以可以从右向左遍历；
如果按照左边界排序，还从左向右遍历的话，其实也可以，逻辑会有所不同；

题意就是求非交叉区间的最大个数！

一些同学做这道题目可能真的去模拟去重复区间的行为，这是比较麻烦的，还要去删除区间。题目只是要求移除区间的个数，没有必要去真实的模拟删除区间！

按照右边界排序，从左向右记录非交叉区间的个数。最后用区间总数减去非交叉区间的个数就是需要移除的区间个数了。此时问题就是要求非交叉区间的最大个数。

贪心算法的思想

右边界排序之后：

局部最优：优先选右边界小的区间，所以从左向右遍历，留给下一个区间的空间大一些，从而尽量避免交叉；
全局最优：选取最多的非交叉区间。
局部最优推出全局最优，试试贪心！

这里记录非交叉区间的个数还是有技巧的，如图：

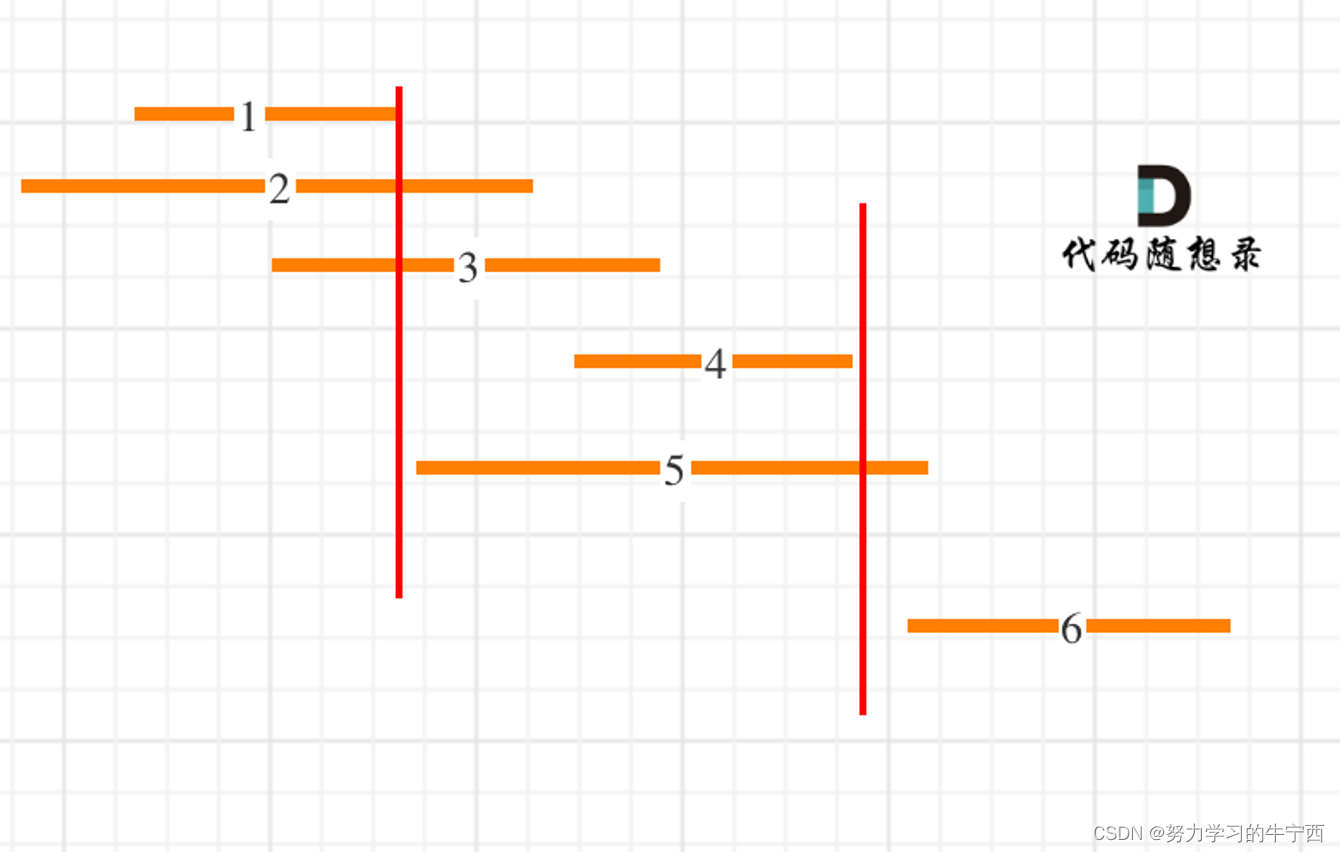
区间，1，2，3，4，5，6都按照右边界排好序。

每次取非交叉区间的时候，都是可右边界最小的来做分割点（这样留给下一个区间的空间就越大），所以第一条分割线就是区间1结束的位置；

接下来就是找大于区间1结束位置的区间，是从区间4开始。那有同学问了为什么不从区间5开始？别忘已经是按照右边界排序的了；

区间4结束之后，在找到区间6，所以一共记录非交叉区间的个数是三个；总共区间个数为6，减去非交叉区间的个数3。移除区间的最小数量就是3。

2. 代码实现

# 贪心算法
# time:O(NlogN);space:O(n)
class Solution(object):
    def eraseOverlapIntervals(self, intervals):
        """
        :type intervals: List[List[int]]
        :rtype: int
        """
        # 细节:当x[1]相同的时候，随便排序都可以，不影响结果
        intervals.sort(key = lambda x: x[1])
        # 记录非交叉区间的个数
        count = 1
        # 记录区间分割点
        rightLine = intervals[0][1]
        for i in range(1,len(intervals)):
            if intervals[i][0] >= rightLine:
                count += 1
                rightLine = intervals[i][1]
        return len(intervals)-count

3. 复杂度分析

时间复杂度：O(nlog n) ，有一个快排；
空间复杂度：O(n)，有一个快排，最差情况(倒序)时，需要n次递归调用。因此确实需要O(n)的栈空间；

4. 思考与收获

本题难度级别可以算是hard级别的！

总结如下难点：
- 难点一：一看题就有感觉需要排序，但究竟怎么排序，按左边界排还是右边界排。
- 难点二：排完序之后如何遍历，如果没有分析好遍历顺序，那么排序就没有意义了。
- 难点三：直接求重复的区间是复杂的，转而求最大非重复区间个数。
- 难点四：求最大非重复区间个数时，需要一个分割点来做标记。
这四个难点都不好想，但任何一个没想到位，这道题就解不了；
贪心就是这样，代码有时候很简单（不是指代码短，而是逻辑简单），但想法是真的难！这和动态规划还不一样，动规的代码有个递推公式，可能就看不懂了，而贪心往往是直白的代码，但想法读不懂，哈哈；
本题其实和**452.用最少数量的箭引爆气球 (opens new window)** 非常像，弓箭的数量就相当于是非交叉区间的数量，只要把弓箭那道题目代码里射爆气球的判断条件加个等号（认为[0，1][1，2]不是相邻区间），然后用总区间数减去弓箭数量就是要移除的区间数量了。

Reference：代码随想录 (programmercarl.com)

本题学习时间：40分钟。

LeetCode763. 划分字母区间

链接：763. 划分字母区间 - 力扣（LeetCode）

1. 思路

一想到分割字符串就想到了回溯，但本题其实不用回溯去暴力搜索；题目要求同一字母最多出现在一个片段中，那么如何把同一个字母的都圈在同一个区间里呢？

如果没有接触过这种题目的话，还挺有难度的。

在遍历的过程中相当于是要找每一个字母的边界，如果找到之前遍历过的所有字母的最远边界，说明这个边界就是分割点了。此时前面出现过所有字母，最远也就到这个边界了。

可以分为如下两步：

统计每一个字符最后出现的位置
从头遍历字符，并更新字符的最远出现下标，如果找到字符最远出现位置下标和当前下标相等了，则找到了分割点

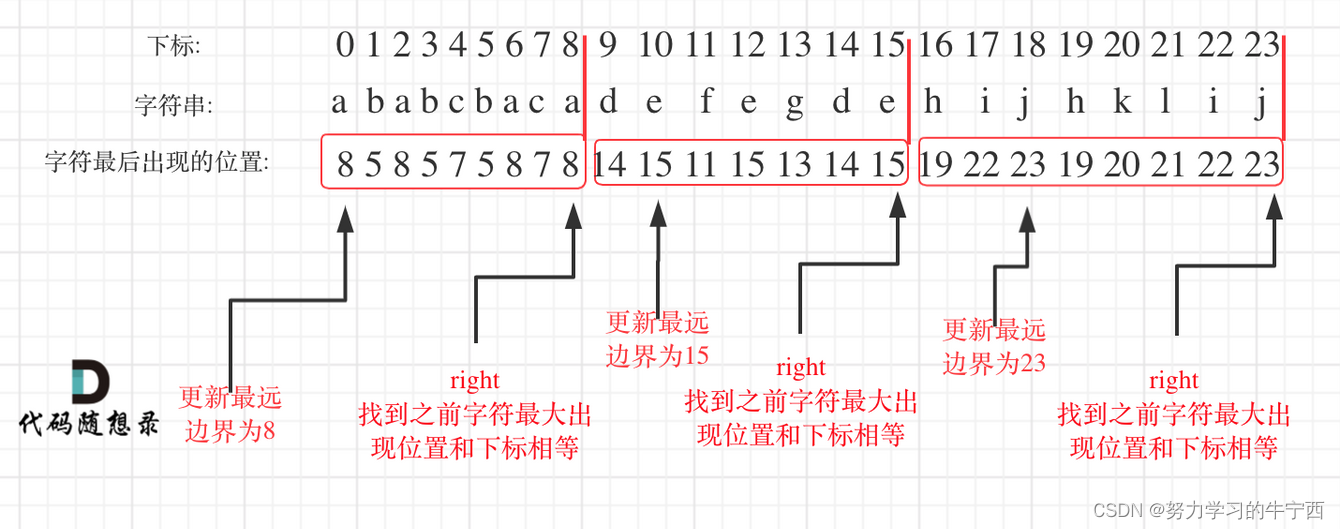
2. 代码实现

# 贪心算法
# time:O(N);space:O(1)
class Solution(object):
    def partitionLabels(self, s):
        """
        :type s: str
        :rtype: List[int]
        """
        # i为字符，hash[i]为字符出现的最后位置
        record = [0]*26
        result = []
        left = 0
        right = 0
        # 统计每一个字符最后出现的位置
        for i in range(len(s)):
            record[ord(s[i])-ord("a")] = i
        for i in range(len(s)):
            # 找到字符出现的最远边界
            right = max(right,record[ord(s[i])-ord("a")])
            if i == right:
                result.append(right-left+1)
                left = i+1
        return result

3. 复杂度分析

时间复杂度：O(N)

其中N为字符串长度的大小，需要遍历字符串两遍；
空间复杂度：O(1）

使用的hash数组的大小是固定的；

4. 思考与收获

这道题目leetcode标记为贪心算法，说实话，我没有感受到贪心，找不出局部最优推出全局最优的过程。就是用最远出现距离模拟了圈字符的行为，但这道题目的思路是很巧妙的！

(二刷再看）这里提供一种与**452.用最少数量的箭引爆气球 (opens new window)、435.无重叠区间 (opens new window)相同的思路。统计字符串中所有字符的起始和结束位置，记录这些区间(实际上也就是435.无重叠区间 (opens new window)**题目里的输入)，将区间按左边界从小到大排序，找到边界将区间划分成组，互不重叠。找到的边界就是答案。

class Solution {
public:
    static bool cmp(vector<int> &a, vector<int> &b) {
        return a[0] < b[0];
    }
    // 记录每个字母出现的区间
    vector<vector<int>> countLabels(string s) {
        vector<vector<int>> hash(26, vector<int>(2, INT_MIN));
        vector<vector<int>> hash_filter;
        for (int i = 0; i < s.size(); ++i) {
            if (hash[s[i] - 'a'][0] == INT_MIN) {
                hash[s[i] - 'a'][0] = i;
            }
            hash[s[i] - 'a'][1] = i;
        }
        // 去除字符串中未出现的字母所占用区间
        for (int i = 0; i < hash.size(); ++i) {
            if (hash[i][0] != INT_MIN) {
                hash_filter.push_back(hash[i]);
            }
        }
        return hash_filter;
    }
    vector<int> partitionLabels(string s) {
        vector<int> res;
        // 这一步得到的 hash 即为无重叠区间题意中的输入样例格式：区间列表
        // 只不过现在我们要求的是区间分割点
        vector<vector<int>> hash = countLabels(s);
        // 按照左边界从小到大排序
        sort(hash.begin(), hash.end(), cmp);
        // 记录最大右边界
        int rightBoard = hash[0][1];
        int leftBoard = 0;
        for (int i = 1; i < hash.size(); ++i) {
            // 由于字符串一定能分割，因此,
            // 一旦下一区间左边界大于当前右边界，即可认为出现分割点
            if (hash[i][0] > rightBoard) {
                res.push_back(rightBoard - leftBoard + 1);
                leftBoard = hash[i][0];
            }
            rightBoard = max(rightBoard, hash[i][1]);
        }
        // 最右端
        res.push_back(rightBoard - leftBoard + 1);
        return res;
    }
};

Reference：代码随想录 (programmercarl.com)

本题学习时间：40分钟。

Leetcode 56. 合并区间

链接：56. 合并区间 - 力扣（LeetCode）

1. 思路

大家应该都感觉到了，此题一定要排序，那么按照左边界排序，还是右边界排序呢？都可以！

那么我按照左边界排序：

排序之后局部最优：每次合并都取最大的右边界，这样就可以合并更多的区间了；
整体最优：合并所有重叠的区间。
局部最优可以推出全局最优，找不出反例，试试贪心。

如何判断重复？

那有同学问了，本来不就应该合并最大右边界么，这和贪心有啥关系？有时候贪心就是常识！哈哈

按照左边界从小到大排序之后，如果 intervals[i][0] < intervals[i - 1][1] 即intervals[i]左边界 < intervals[i - 1]右边界，则一定有重复，因为intervals[i]的左边界一定是大于等于intervals[i - 1]的左边界。

即：intervals[i]的左边界在intervals[i - 1]左边界和右边界的范围内，那么一定有重复！

这么说有点抽象，看图：（注意图中区间都是按照左边界排序之后了）

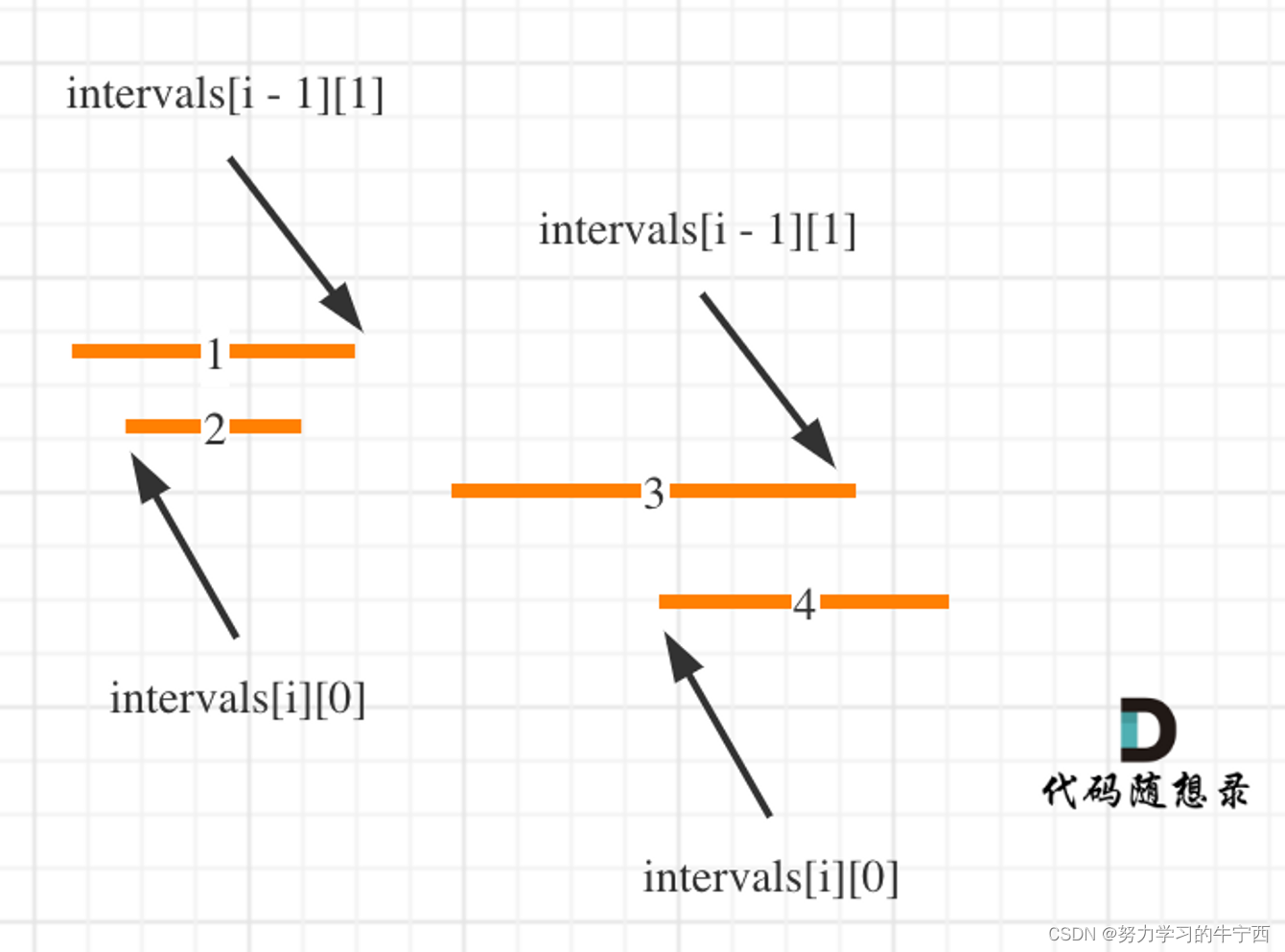
如何模拟合并区间呢？

其实就是用合并区间后左边界和右边界，作为一个新的区间，加入到result数组里就可以了。如果没有合并就把原区间加入到result数组。

2. 代码实现

# 贪心算法
# time:O(NlogN);space:O(N)
class Solution(object):
    def merge(self, intervals):
        """
        :type intervals: List[List[int]]
        :rtype: List[List[int]]
        """
        # 按照区间左边界从小到大排序
        intervals.sort(key=lambda x: x[0])
        # 先初始化result的第一个元素为第一个intervals里面的区间
        result= [intervals[0]]
        # 从第二个区间开始遍历intervals
        for i in range(1,len(intervals)):
            # 如果当前interval的左边界小于或者等于
            # result最后一个元素的右边界，说明有重叠区间
            if intervals[i][0] <= result[-1][1]:
                # 合并区间，左边界因为排序了，所以不变
                # 更新右边界，为以前值和现在的值的最大值
                result[-1][1] = max(result[-1][1],intervals[i][1])
            else:
                # 如果最后一个区间没有合并，将其加入result
                result.append(intervals[i])
        return result

3. 复杂度分析

时间复杂度：O(nlog n)

其中N为intervals数组的长度，有一个快排；
空间复杂度：O(n)

有一个快排，最差情况(倒序)时，需要n次递归调用。因此确实需要O(n)的栈空间；

4. 思考与收获

对于贪心算法，很多同学都是：如果能凭常识直接做出来，就会感觉不到自己用了贪心, 一旦第一直觉想不出来, 可能就一直想不出来了。跟着「代码随想录」刷题的录友应该感受过，贪心难起来，真的难。那应该怎么办呢？

正如我贪心系列开篇词**关于贪心算法，你该了解这些！ (opens new window)**中讲解的一样，贪心本来就没有套路，也没有框架，所以各种常规解法需要多接触多练习，自然而然才会想到。「代码随想录」会把贪心常见的经典题目覆盖到，大家只要认真学习打卡就可以了。

Reference：代码随想录 (programmercarl.com)

本题学习时间：40分钟。

本篇学习时间约为2小时，总结字数为5000+；本篇是贪心算法的重叠区间专题，再加上Day35的最后一道题：用最少数量的箭引爆气球，这四道题是重叠区间的经典题目，都属于那种看起来好复杂，但一看贪心解法，惊呼：这么巧妙！做过了也就会了，没做过就很难想出来。（求推荐！）