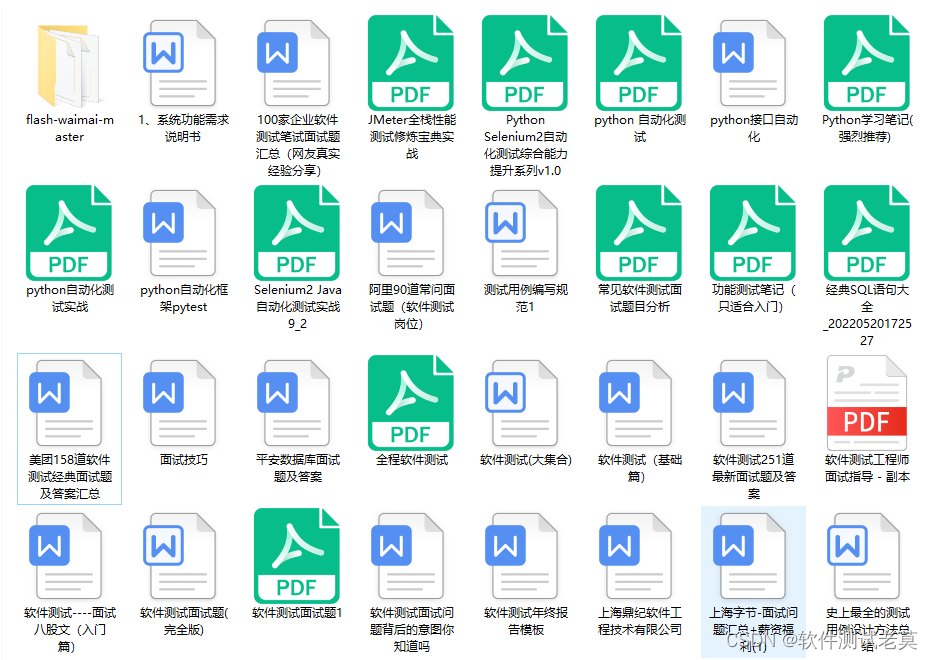
截至周三刷了六道题
题目1:
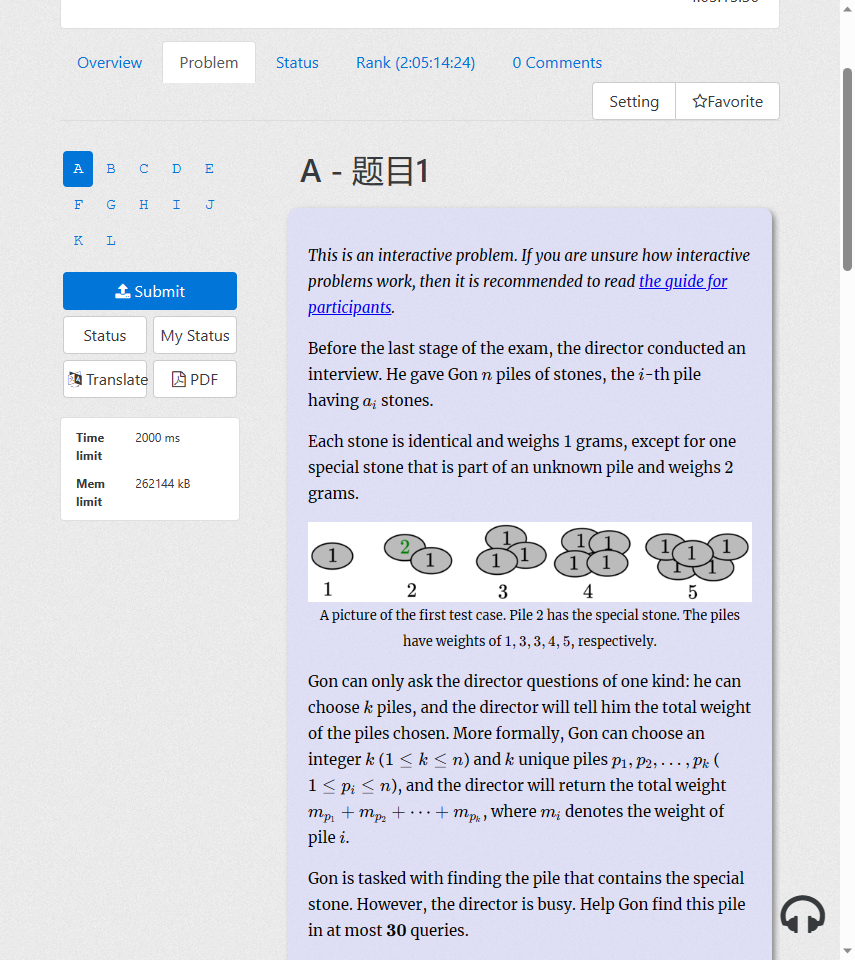
这是个交互题,目前遇到的交互题都是用二分解决的。
本题使用二分精准定位拥有重量为2的石头的堆。
为避免时间超限,应该再输入数据时计算好前缀和。
二分过程中,如果哪边的重量总和不等于石头数,那就向这边缩小范围。
代码:

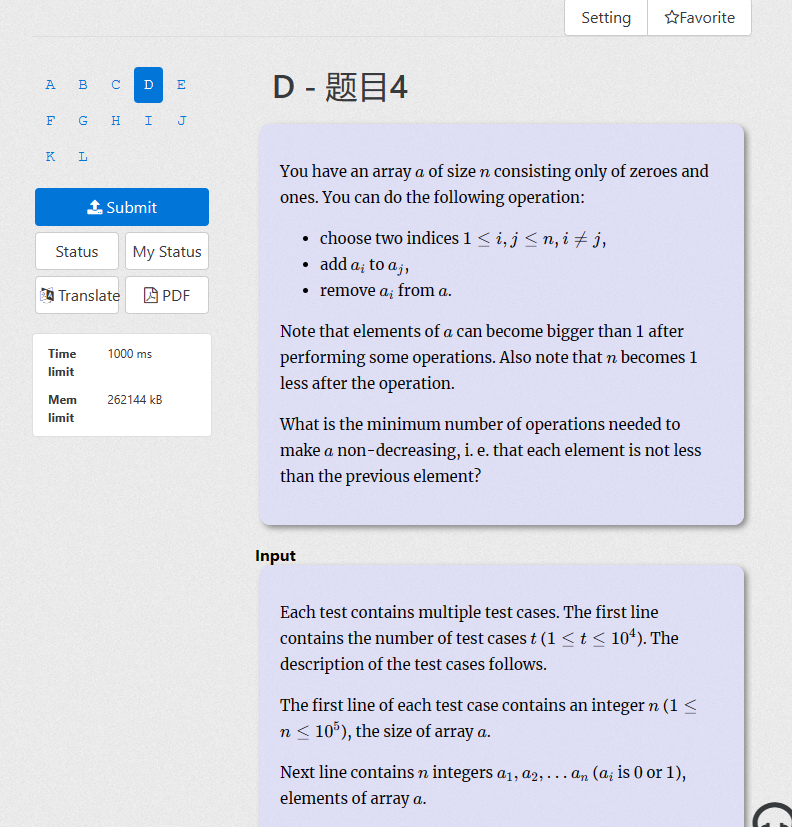
这道题非常简单,只需要找出规律就行
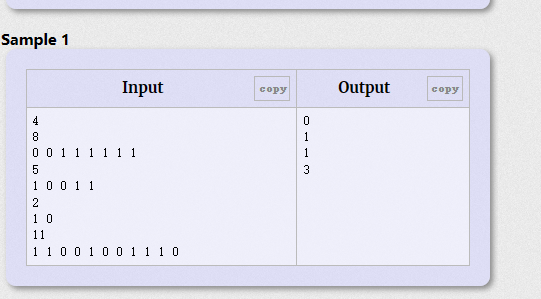
序列只由0或1组成,我们可以进行的操作是,删除一个数加到另一个数上面去。
删0加0 《=》只删除了一个障碍0,另一个0无动于衷
删0加1 《=》删除了一个障碍0
删1加1 《=》变出了一个2,浪费时间浪费资源浪费精力没必要
删1加0 《=》删除了一个前面的障碍0和后面的障碍1
所以我们就需要采用删1加0的方式操作数列
很容易发现,我们只需要遍历整个序列一共有多少个0,假设是n个0,那么再遍历前n个数,遇到1则ans加1,相当于用前n个里的1去消除掉后面的0。
所以代码呼之欲出:

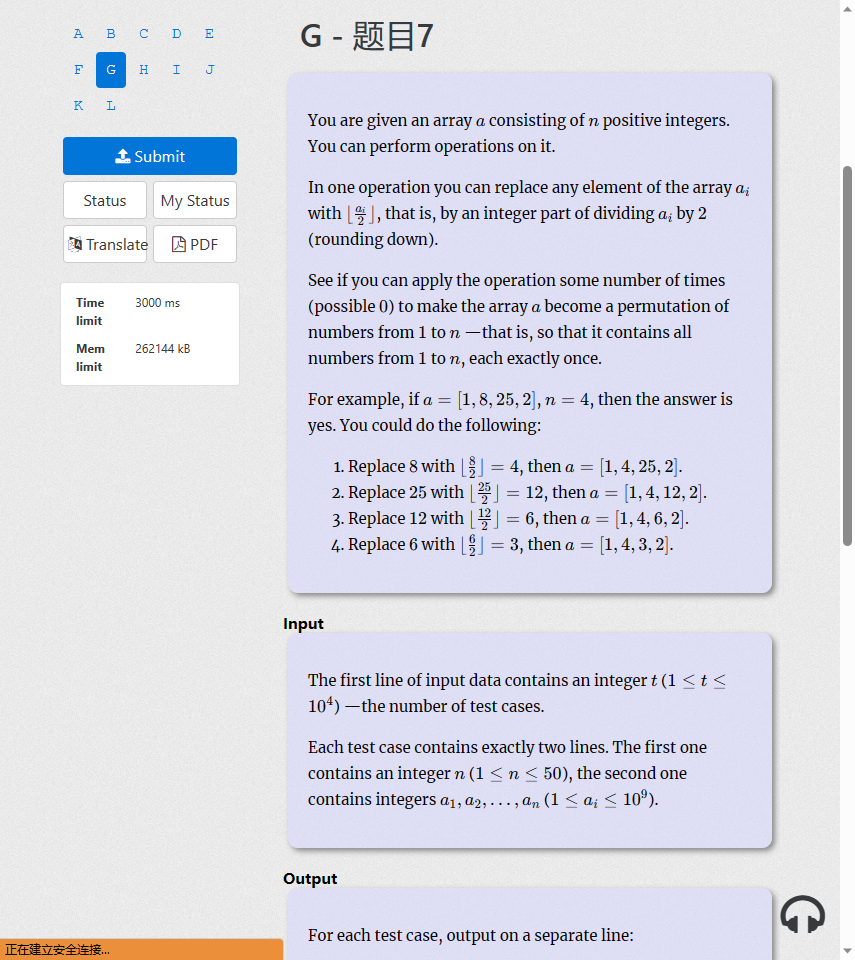
这道题就是要通过/2的操作使得序列变成1~n的全排列。
1~n的全排列即1到n且互不相等,且所有数小于n
所以我们只需要遍历所有数,如果大于n就往下除2得新值。
且不能在1~n中重复,这里需要一个标记数组就行了。
如果最后1~n的标记均为1(即都有值入坑了0),那就输出YES,否则输出NO
代码如下:

这道题不要被样例给迷惑了,其实超级简单
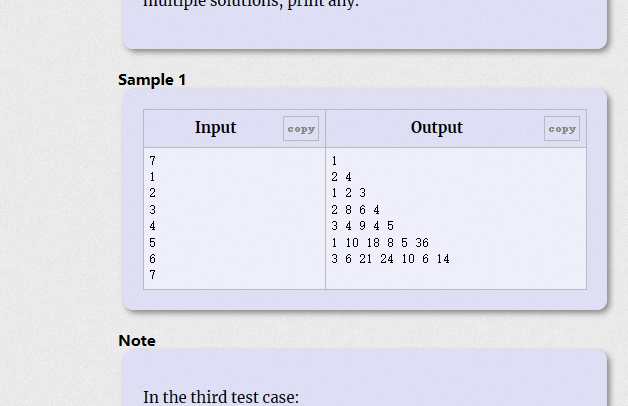
第i个数必须是i的n倍(n=1~xxxx)
且数列所有值的和必须能整除n
而第一个数,i=1,所以第一个数可以随意取,那么其他位置上的数我们只需要取i本身就行(相当于取了i的1倍,符合要求),那么第一个数取多少取决于该条件 且数列所有值的和必须能整除n
所以满足(sum(后面的数)+a【1】)%n = 0即可。
所以代码:
这道题倒是写了挺久,因为总是漏掉情况
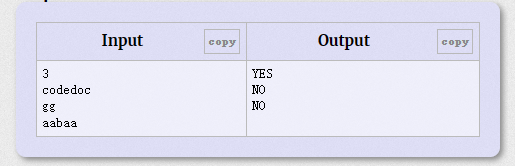
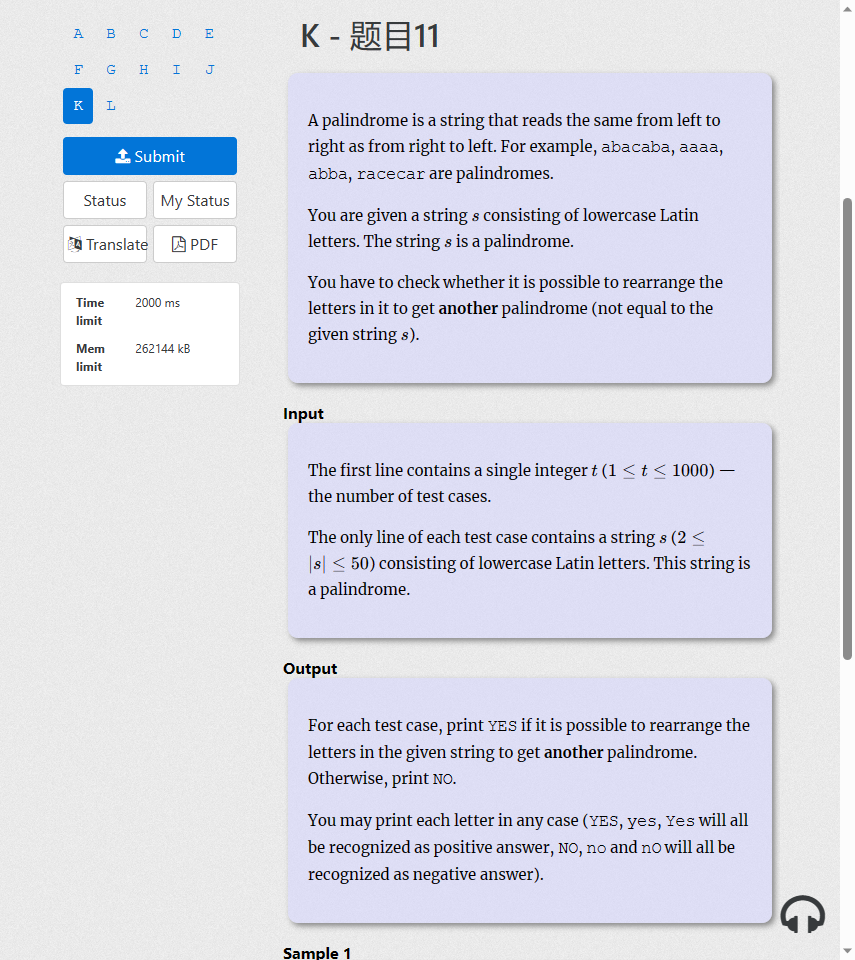
题目就是问给出的字符串能否通过重新排序变成回文字符串(且不能和本身一样)
那么只需要考虑几种情况
1.重组不成回文字符串
2.符合回文字符串条件但只有一种情况且与本身重复
3.符合回文字符串条件且有多种组成方式
我们需要对字符串长度的奇偶进行判断,以及每个字母出现的次数(要用到出现次数的奇偶性)
重点看注释
代码:
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
ll t,cnt,ji,ncnt,u;
string s;
bool huiwen(string s)
{
for(int i=0,j=s.size()-1; i!=j; i++,j--)
if(s[i]!=s[j])
return false;
return true;
}
int main()
{
cin>>t;
while(t--)
{
cin>>s;
map<char,int> m;
char c[50];
cnt=0;
for(int i=0; i<s.size(); i++)
{
if(m[s[i]]==0)
{
c[cnt]=s[i];
cnt++;
}
m[s[i]]++;
}
//测试
//for(int i=0; i<cnt; i++){
// cout<<"第"<<i+1<<"个字母是"<<c[i]<<endl;
// cout<<"有"<<m[c[i]]<<"个"<<endl;
//}
if(cnt==1)//只有一种字母
{
cout<<"NO"<<endl;
continue;
}
ji=0;//统计有多少奇数个数的字母
u=0;
for(int i=0; i<cnt; i++)
{
if(m[c[i]]%2!=0)
{
ji++;
u=m[c[i]];
}
}
ncnt=s.size();//字符串长度
if(ncnt%2==1)//奇数长度
{
if(ji==1 &&cnt==2&& u==1 && huiwen(s))cout<<"NO"<<endl;
else if(ji>=1 && ncnt%2==0 )cout<<"NO"<<endl;
else if(ji>1)cout<<"NO"<<endl;
else cout<<"YES"<<endl;
}
else if(ncnt%2==0) //偶数长度
{
if(ji!=0)cout<<"NO"<<endl;
else cout<<"YES"<<endl;
}
}
return 0;
}
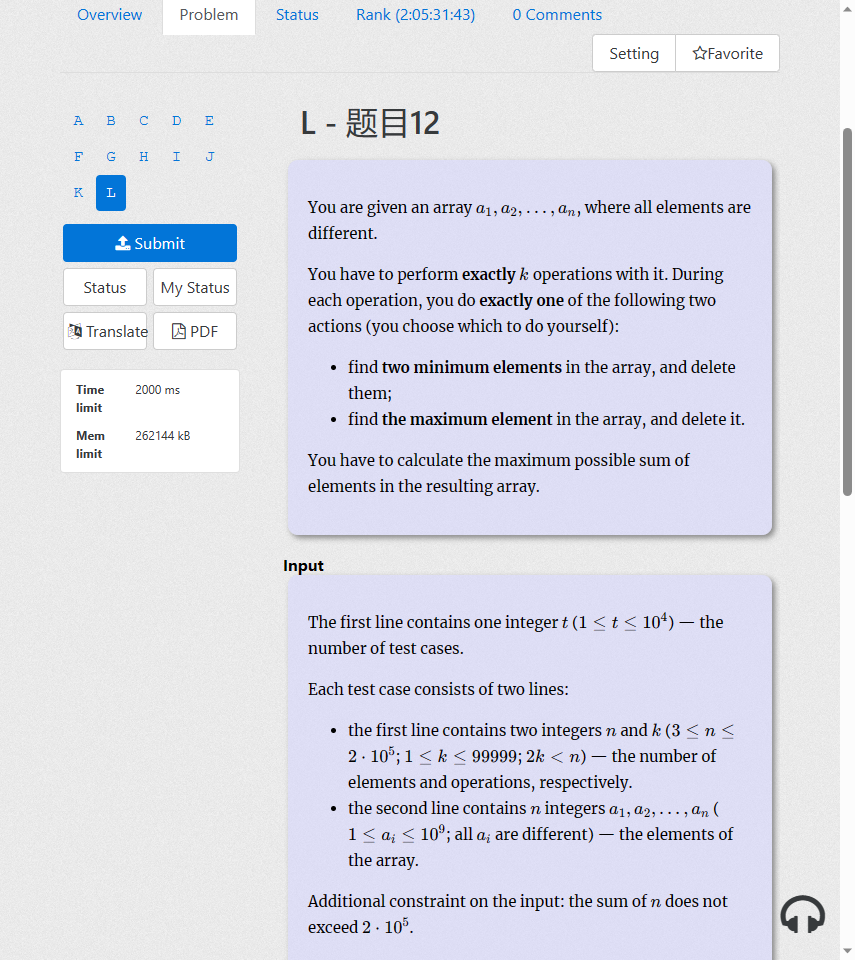
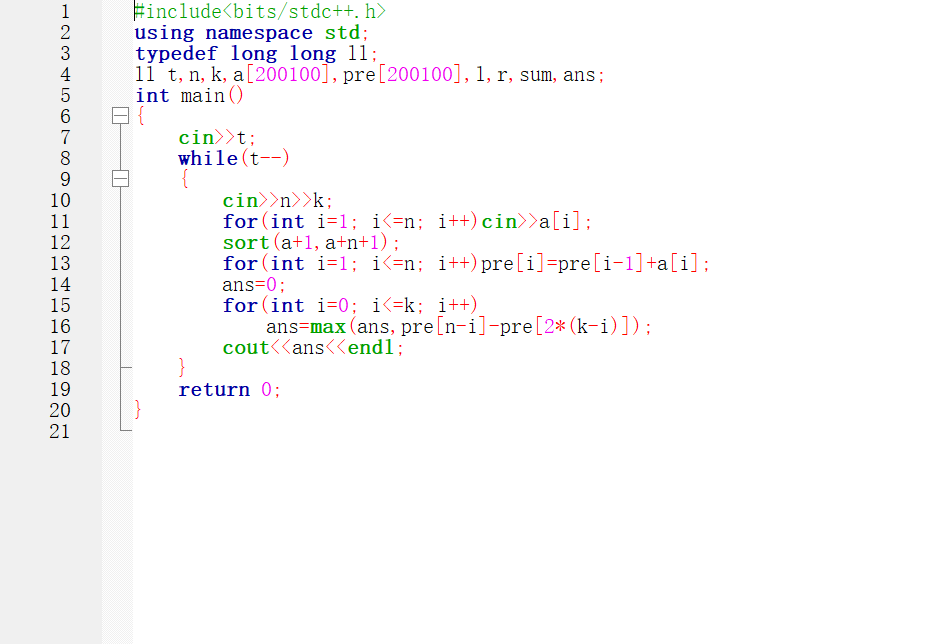
这道题怎么说呢,可以说是暴力解决的,只需要枚举可执行方案就行,然后找出能得到最大值的方案,输出该最大值。
因为只有两种操作,即删除最小的两个数或者删除最大的一个数,这样的题目我们很容易想到先进行一个sort排序,那么删除哪个数也就是维护两端端点就行了。
一开始枚举每种情况计算两端点,再将两端点之间进行相加,可以过样例,但是会时间超限。
所以后面在排完序计算了前缀和,最后之间用前缀和计算总和过的。
代码很简单:
好,这就是前两天做的六道题的题解。