( 动态规划) 509. 斐波那契数 ——【Leetcode每日一题】

news2025/1/7 6:06:57

❓509. 斐波那契数

难度：简单

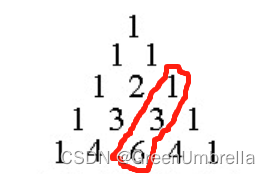
斐波那契数 （通常用 F(n) 表示）形成的序列称为 斐波那契数列 。该数列由 0 和 1 开始，后面的每一项数字都是前面两项数字的和。也就是：

F(0) = 0，F(1) = 1
F(n) = F(n - 1) + F(n - 2)，其中 n > 1

给定 n ，请计算 F(n) 。

示例 1：

输入：n = 2
输出：1
解释：F(2) = F(1) + F(0) = 1 + 0 = 1

示例 2：

输入：n = 3
输出：2
解释：F(3) = F(2) + F(1) = 1 + 1 = 2

示例 3：

输入：n = 4
输出：3
解释：F(4) = F(3) + F(2) = 2 + 1 = 3

提示：

0 <= n <= 30

💡思路：动态规划

斐波那契数的边界条件是 F(0) = 0 和 F(1) = 1。当 n > 1 时，每一项的和都等于前两项的和，因此有如下递推关系：
$F (n) = F (n - 1) + F (n - 2)$

由于斐波那契数存在递推关系，因此可以使用动态规划求解。动态规划的状态转移方程即为上述递推关系，边界条件为 F(0) 和 F(1)。

根据状态转移方程和边界条件，可以得到时间复杂度和空间复杂度都是 $O (n)$ 的实现。由于 F(n) 只和 F(n−1) 与 F(n−2) 有关，因此可以使用「滚动数组思想」把空间复杂度优化成 O(1)。

🍁代码：(Java、C++)

Java

class Solution {
    public int fib(int n) {
        if(n <= 1) return n;
        int f1 = 0, f2 = 1;
        int ans = 0;
        for(int i = 2; i <= n; i++){
            ans = f1 + f2;
            f1 = f2;
            f2 = ans;
        }
        return ans;
    }
}

C++

class Solution {
public:
    int fib(int n) {
        if(n <= 1) return n;
        int f1 = 0, f2 = 1;
        int ans = 0;
        for(int i = 2; i <= n; i++){
            ans = f1 + f2;
            f1 = f2;
            f2 = ans;
        }
        return ans;
    }
};