前言
数据结构是一个古老的课题。他与程序开发息息相关,但是我们日常开发中,好像很少让我们自己设计一个数据结构。只求程序能跑,并不太关注性能。但是它是我们软件开发人员的基本功,也是拉开普通程序员和高级程序员的一个门槛,是大厂面试必不可少的一部分。
本节,我们就数据结构和算法做个简单概述,后续会在数据结构专栏,逐一介绍。
1.数据结构简介
1.1 什么是数据结构
数据结构(data structure)是计算机存储、组织数据的方式。数据结构是指相互之间存在一种或多种特定关系的数据元素的集合。(百度百科)
通俗的讲,就是在内存中存储管理数据的方式。
1.2 数据结构分类
1.2.1 逻辑结构
逻辑结构是用来描述数据元素之间的逻辑关系,是一个抽象概念,与数据的实际存储无关,独立于计算机存在。
1.2.2 存储结构
存储结构是数据元素及其相互之间的关系在计算机存储器中的存储方式,简而言之存储结构就是实际的物理存储方式。
1.2.3 两者关系
逻辑结构是数据结构的抽象,物理结构是数据结构的实现,两者综合起来才建立了数据元素完整的结构关系,只有逻辑结构,数据无法实际存储;只有物理结构,数据不知道该用哪种合适的方式存储。
笔者认为,这个就像软件设计环节,先有概要设计,ER图维护实体之间的关系,类似逻辑结构,等详细设计的时候,具体定义表结构,要考虑表怎么加索引等,即存储结构,数据在磁盘中怎么管理。
1.3 逻辑结构分类
1.3.1 线性结构
数据结构中线性结构指的是数据元素之间存在着“一对一“的线性关系的数据结构。
1.3.2 集合结构
所有数据元素除了同属于一个集合外,并无其他关系。集合结构的集合中任何两个数据元素之间都没有逻辑关系,组织形式松散。
1.3.3 树状结构
树状结构是一个或多个节点的有限集合,数据元素之间存在“一对多”的层次关系。
1.3.4 网状结构
数据元素之间存在“多对多的关系”(注:此时的“多对多”中的多表示,至少有一个)
1.4 存储结构分类
1.4.1 顺序存储结构
把逻辑上相邻的节点存储在物理位置上相邻的存储单元里,节点之间的逻辑关系有存储单元的邻接关系来体现。
优点:节省存储空间
缺点:不便于修改
1.4.2 链式存储结构
不要求逻辑上相邻的节点在物理位置上也相邻,节点间的逻辑关系是由附加的指针字段表示的。
优点:便于修改
缺点:存储空间的利用率低、不能对节点进行随机存取。
1.4.3 索引存储结构
在存储节点信息的同时,建立附件的索引表。
优点:大大提高了数据查找的速度
缺点:增加了索引表、因而降低了存储空间的利用率。
1.4.4 散列存储结构
根据节点的关键字通过哈希(或散列)函数直接计算出一个值,并将这个 值作为该节点的存储地址,适合于要求对数据进行快速查找和插入的场合。
优点:查找速度快
缺点:由于哈希存储方法只存储节点的数据,不存储节点之间的逻辑关系。
1.5 常见数据结构
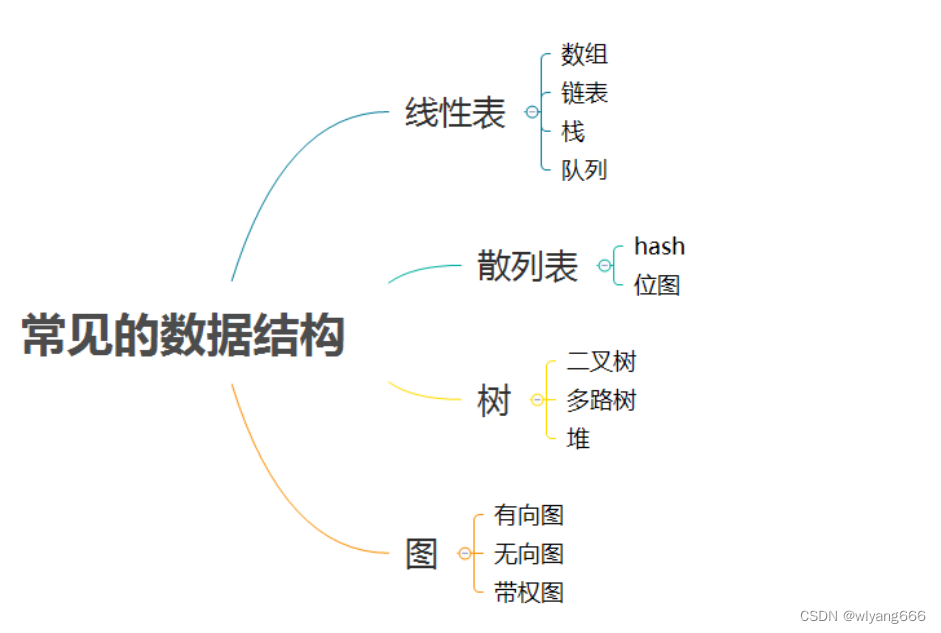
后续会在数据结构专栏详细逐个介绍相关数据结构。
2. 算法简介
2.1 什么是算法
算法(Algorithm)是指解题方案的准确而完整的描述,是一系列解决问题的清晰指令,算法代表着用系统的方法描述解决问题的策略机制。一句话描述:算法是一种解决特定问题的思路
2.2 时间复杂度
2.2.1 什么是时间复杂度
判断一个算法所编程序运行时间的多少,并不是将程序编写出来,通过在计算机上运行所消耗的时间来度量。原因很简单,一方面,解决一个问题的算法可能有很多种,一一实现的工作量无疑是巨大的,得不偿失;另一方面,不同计算机的软、硬件环境不同,即便使用同一台计算机,不同时间段其系统环境也不相同,程序的运行时间很可能会受影响,严重时甚至会导致误判。
实际场景中,我们更喜欢用一个估值来表示算法所编程序的运行时间。所谓估值,即估计的、并不准确的值。注意,虽然估值无法准确的表示算法所编程序的运行时间,但它的得来并非凭空揣测,需要经过缜密的计算后才能得出。
也就是说,表示一个算法所编程序运行时间的多少,用的并不是准确值(事实上也无法得出),而是根据合理方法得到的预估值。
计算的方式就是时间复杂度。时间复杂度是指执行算法所需要的计算工作量。
2.2.2 复杂度计算方法
复杂度计算可以参考这篇博客
2.2.3 常用的时间复杂度
常数阶O(1)
对数阶O(logN)
线性阶O(n)
线性对数阶O(nlogN)
平方阶O(n²)
立方阶O(n³)
K次方阶O(n^k)
指数阶(2^n)
2.3 空间复杂度
空间复杂度全称是渐进空间复杂度,表示算法的存储空间与数据规模之间的增长关系。指执行这个算法所需要的内存空间。由于现在硬件相对比较便宜,所以在开发中常常会利用空间来换时间,比如缓存技术。典型的数据结构中空间换时间是:跳跃表
在实际开发中会更关注代码的时间复杂度,而不是空间复杂度
2.4 常见算法
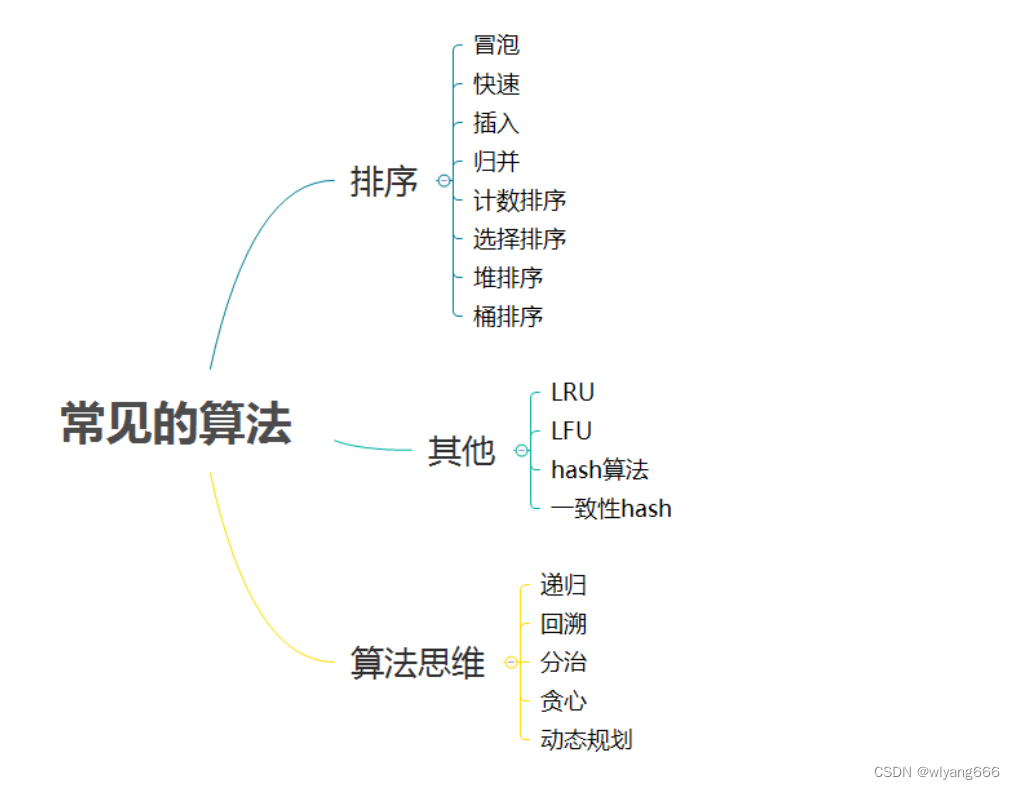
后续会在数据结构专栏详细逐个介绍相关算法。