什么是二叉树

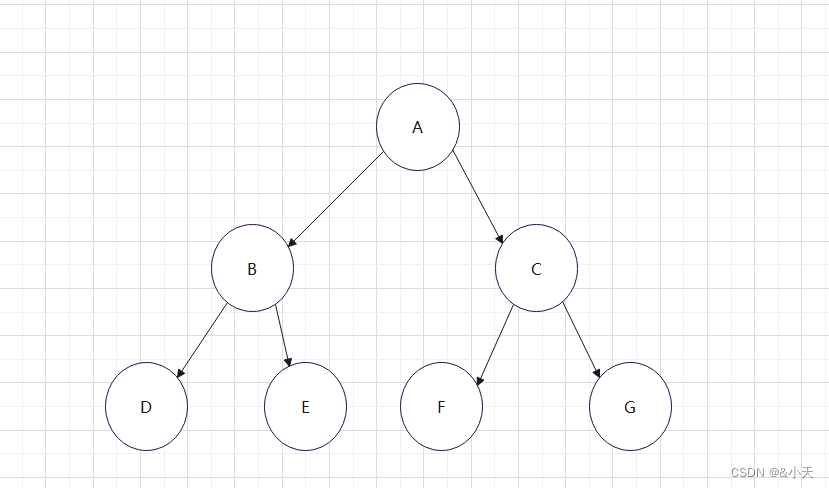
二叉树（Binary tree）是树形结构的一个重要数据类型，想要成为二叉树必须满足两个条件。1、本身是有序树。2、树中包含的各个节点的度不能超过 2。

如图：
该图就是一个二叉树，满足了是有序树，也满足树的度数。

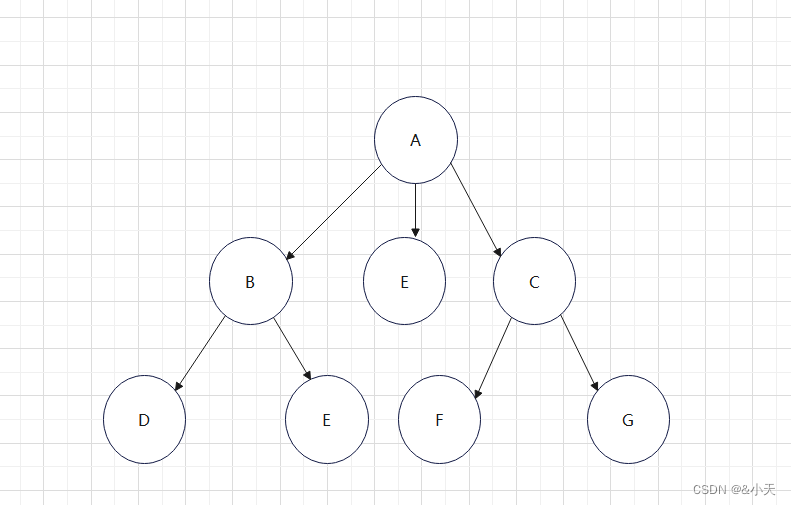
下面这个图就不是二叉树：

二叉树的特殊类型

二叉树的特殊类型有满二叉树和完全二叉树。

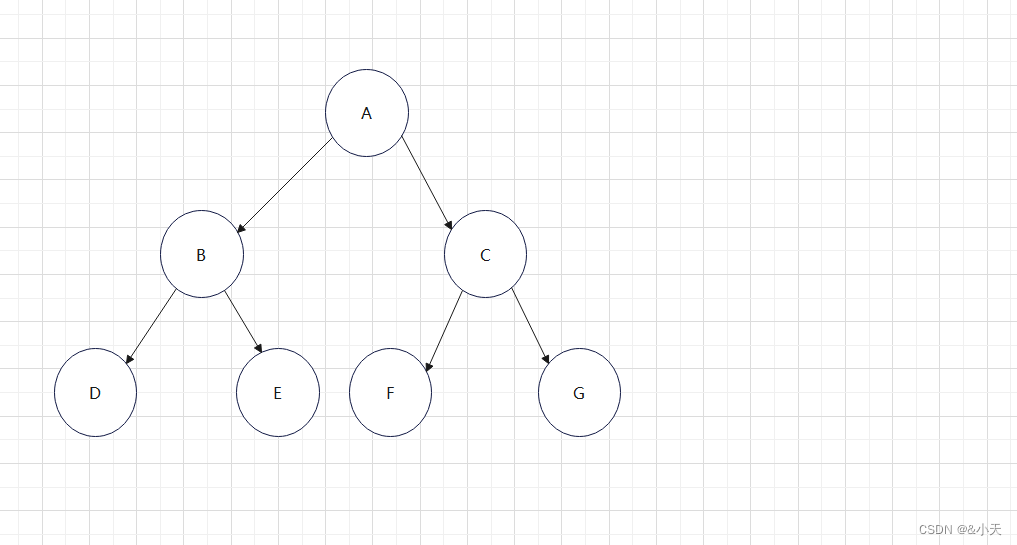
如图：该图就是满二叉树，满叉树就是如果每一个层的结点数都达到最大值，则这个二叉树就是满二叉树。

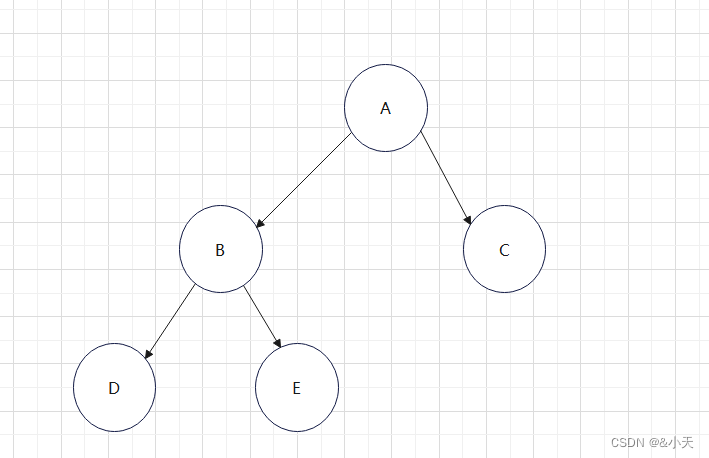
如图：该图就是完全二叉树，完全二叉树是满二叉树演变而来的它的特点是假设有h层，h-1层是全满的，h层从左到右是没有满的则为完全二叉树。

二叉树的遍历方式

二叉树的常见遍历方式先序，中序，后序。
先序是：利用分治思想将树分为根和子树，先走根节点然后走左子树，然后再走右子树。
中序则是：先从左子树出发然后根节点，然后再右子树。
后序则是：先从左子树走再走右子树，最后走根。

下面上代码：

#include<iostream>
using namespace std;
typedef char q;
typedef struct shu{
	shu* left;
	shu* right;
	q data;
}shu,*p;
void print1(p c){//打印先序
	if (c == NULL) {
		return;
	}
	cout << c->data;
	print1(c->left);
	print1(c->right);
}
void print2(p c) {//打印中序
	if (c == NULL) {
		return;
	}

	print2(c->left);
	cout << c->data;
	print2(c->right);
}
void print3(p c) {//打印后序
	if (c == NULL) {
		return;
	}

	print3(c->left);
	print3(c->right);
	cout << c->data;
}
int main() {
	p A = new shu;
	A->data = 'A';
	A->left = NULL;
	A->right = NULL;
	p B = new shu;
	B->data = 'B';
	B->left = NULL;
	B->right = NULL;
	p C = new shu;
	C->data = 'C';
	C->left = NULL;
	C->right = NULL;
	p D = new shu;
	D->data = 'D';
	D->left = NULL;
	D->right = NULL;
	p E = new shu;
	E->data = 'E';
	E->left = NULL;
	E->right = NULL;
	A->left = B;
	A->right = C;
	B->left = D;
	B->right = E;
	print1(A);
	cout << endl;
	print2(A);
	cout << endl;
	print3(A);
	cout << endl;
	return 0;
}

二叉树的叶子结点求法

求叶子结点用递归的思路就是看左子树和右子树下面有没有结点，若一个有结点则不是。
代码如下：

int Btnodeysize(Btnode* root) {
	if (root == NULL)
		return 0;
	if (root->left== NULL&&root->right==NULL)
		return 1;
	return Btnodeysize(root->left) + Btnodeysize(root->right);
}

二叉树的高度求法

求二叉树的高度求法思路就是看左子树有没有结点，右子树有没有结点进行比较进而求二叉树的高度。
代码如下:

int Btnodehsize(Btnode* root) {
	if (root == NULL)
		return 0;
	int left = Btnodehsize(root->left); 
	int right = Btnodesize(root->right);
	return left>right? left+ 1 : right+ 1;
}