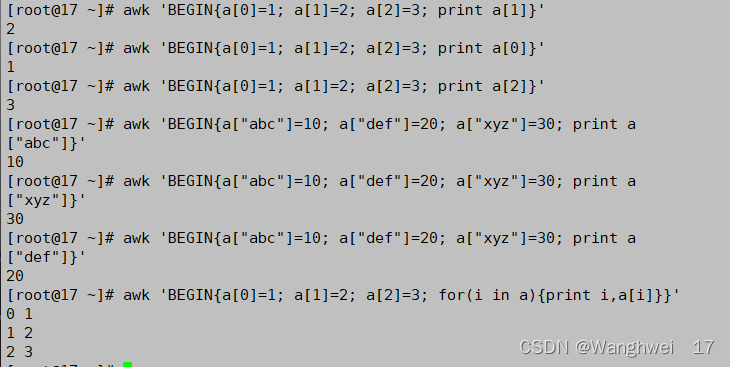
日常鼓励自己：别抱怨努力的苦，那是你去看世界的路。
最近几天一直忙着项目的结项答辩，今天终于是搞完了，得到了老师们的一致好评，最近几天的努力也没白费！现在可以愉快刷题了，先复现下LiteCtf的题目，队伍里的师傅们直接ak了，牛的哇

[LitCTF 2023]梦想是红色的 (初级)

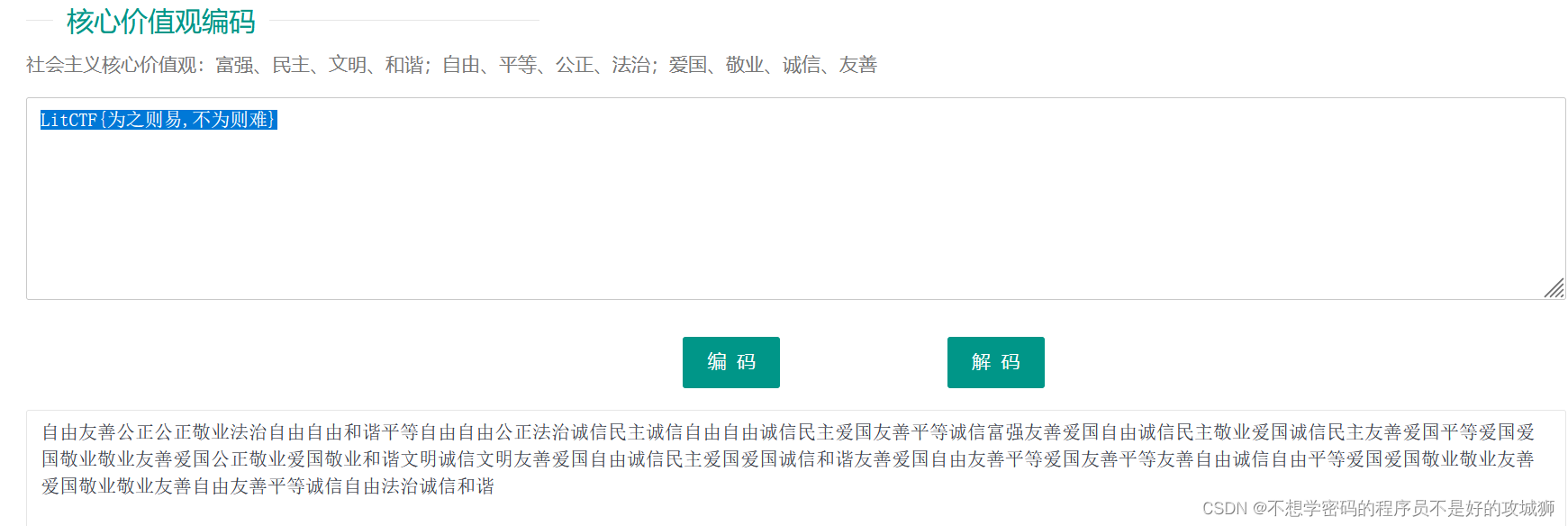
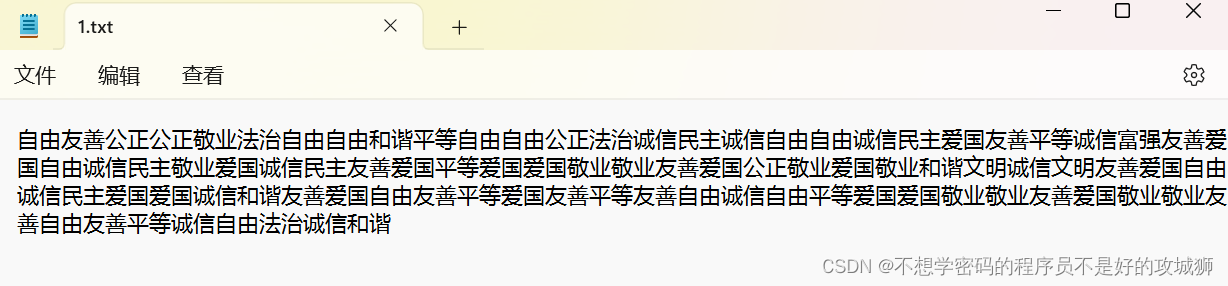如图，打开就是社会主义核心价值观编码，直接在线工具秒了。

[LitCTF 2023]Hex？Hex！(初级)

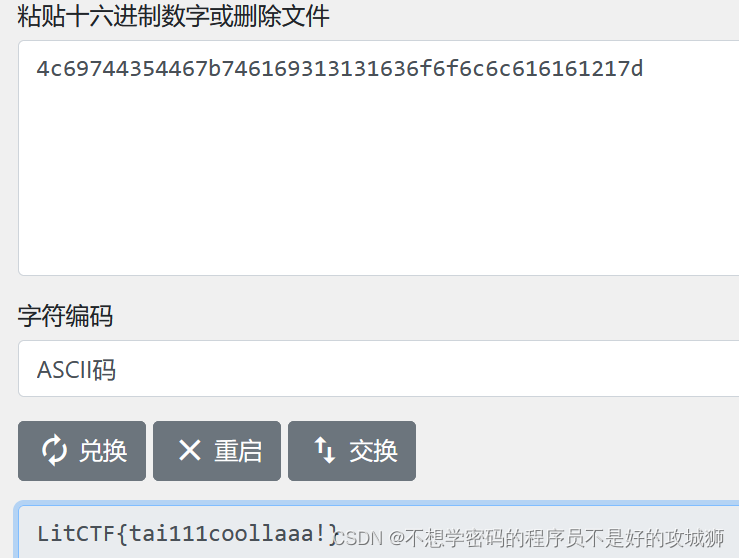
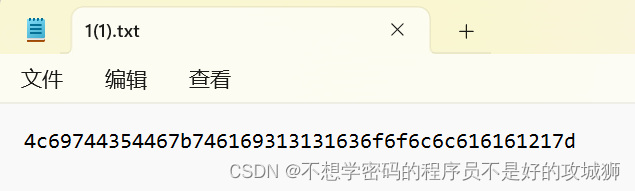打开十六进制，直接秒了

[LitCTF 2023]原来你也玩原神 (初级)

打开是这么一张图，定位到最后一句flag位置，对照密码表进行解密。

[LitCTF 2023]你是我的关键词(Keyworld) (初级)

打开之后是这么一句话，根据题目提示为关键词密码，实不相瞒咱还真不知道是啥玩意，但是根据题目提示，以及猜测flag格式，直接得到答案。

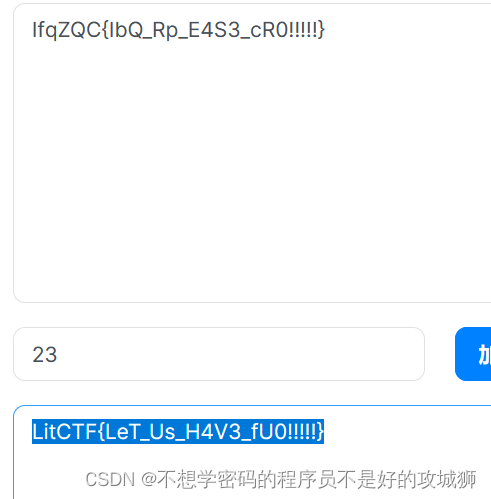
[LitCTF 2023]Is this only base?

1.根据题目提示，尝试栅栏解密(w形)，参数设置为23
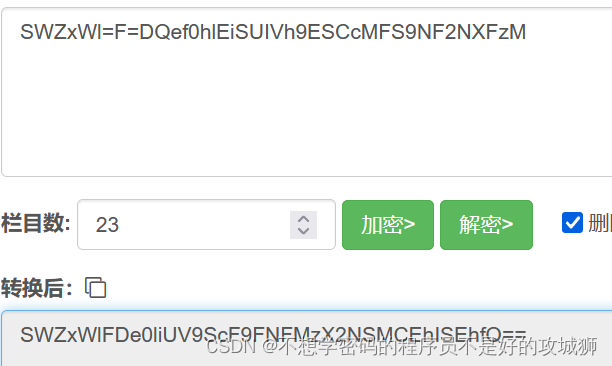2.base64解密
3.凯撒解密

[LitCTF 2023]家人们！谁懂啊，RSA签到都不会 (初级)

from Crypto.Util.number import *
from secret import flag

m = bytes_to_long(flag)
p = getPrime(512)
q = getPrime(512)
e = 65537
n = p*q
c = pow(m,e,n)
print(f'p = {p}')
print(f'q = {q}')
print(f'c = {c}')
'''
p = 12567387145159119014524309071236701639759988903138784984758783651292440613056150667165602473478042486784826835732833001151645545259394365039352263846276073
q = 12716692565364681652614824033831497167911028027478195947187437474380470205859949692107216740030921664273595734808349540612759651241456765149114895216695451
c = 108691165922055382844520116328228845767222921196922506468663428855093343772017986225285637996980678749662049989519029385165514816621011058462841314243727826941569954125384522233795629521155389745713798246071907492365062512521474965012924607857440577856404307124237116387085337087671914959900909379028727767057
'''

！！！签到题也不能直接给出p,q啊
直接上代码吧

import gmpy2
import binascii
p = 12567387145159119014524309071236701639759988903138784984758783651292440613056150667165602473478042486784826835732833001151645545259394365039352263846276073
q = 12716692565364681652614824033831497167911028027478195947187437474380470205859949692107216740030921664273595734808349540612759651241456765149114895216695451

n=p*q

phi=(p-1)*(q-1)

c = 108691165922055382844520116328228845767222921196922506468663428855093343772017986225285637996980678749662049989519029385165514816621011058462841314243727826941569954125384522233795629521155389745713798246071907492365062512521474965012924607857440577856404307124237116387085337087671914959900909379028727767057

e=65537

d=gmpy2.invert(e,phi)

m=pow(c,d,n)

print(binascii.unhexlify(hex(m)[2:]))

#LitCTF{it_is_easy_to_solve_question_when_you_know_p_and_q}

[LitCTF 2023]yafu (中级)

from Crypto.Util.number import *
from secret import flag

m = bytes_to_long(flag)
n  = 1
for i in range(15):
    n *=getPrime(32)
e = 65537
c = pow(m,e,n)
print(f'n = {n}')
print(f'c = {c}')
'''
n = 15241208217768849887180010139590210767831431018204645415681695749294131435566140166245881287131522331092026252879324931622292179726764214435307
c = 12608550100856399369399391849907846147170257754920996952259023159548789970041433744454761458030776176806265496305629236559551086998780836655717
'''

这里的n是15个小素数生成的，考虑直接分解n
下边是一个多素数的RSA

import gmpy2
import binascii
primess=[2151018733,2201440207,2315495107,2719600579,2758708999,2767137487,2906576131,2923522073,3354884521,3355651511,3989697563,4021078331,4044505687,4171911923,2585574697]

n=1

for i in primess:
    n*=i

#print(n==15241208217768849887180010139590210767831431018204645415681695749294131435566140166245881287131522331092026252879324931622292179726764214435307)

c=12608550100856399369399391849907846147170257754920996952259023159548789970041433744454761458030776176806265496305629236559551086998780836655717

phi=1
for i in primess:
    phi*=(i-1)

e=65537
d=gmpy2.invert(e,phi)
m=pow(c,d,n)
print(binascii.unhexlify(hex(m)[2:]))
#LitCTF{Mu1tiple_3m4ll_prim5_fac7ors_@re_uns4f5}

[LitCTF 2023]factordb (中级)

factordb分解之后，直接RSA

[LitCTF 2023]md5的破解

这个也很简单，网上找个脚本几秒跑过了，就先过了吧

[LitCTF 2023]P_Leak

典型的dp泄露
理论部分先不写了，直接代码秒了

from gmpy2 import *

e = 65537
n = 50612159190225619689404794427464916374543237300894011803225784470008992781409447214236779975896311093686413491163221778479739252804271270231391599602217675895446538524670610623369953168412236472302812808639218392319634397138871387898452935081756580084070333246950840091192420542761507705395568904875746222477
c = 39257649468514605476432946851710016346016992413796229928386230062780829495844059368939749930876895443279723032641876662714088329296631207594999580050131450251288839714711436117326769029649419789323982613380617840218087161435260837263996287628129307328857086987521821533565738409794866606381789730458247531619
dp = 5892502924236878675675338970704766304539618343869489297045857272605067962848952532606770917225218534430490745895652561015493032055636004130931491316020329

for x in range(1, e):
    if (e * dp % x == 1):
        p = (e * dp - 1) // x + 1
        if (n % p != 0):
            continue
        q = n // p
        phin = (p - 1) * (q - 1)
        d = invert(e, phin)
        m = powmod(c, d, n)
        if (len(hex(m)[2:]) % 2 == 1):
            continue

        print("m:", m)
        # print(hex(m)[2:])
        print("flag:", bytes.fromhex(hex(m)[2:]))

#flag: b'LitCTF{Prim3_1s_Le@k!!!!!}'

[LitCTF 2023]e的学问

典型的e和phi不互素

from Crypto.Util.number import *
m=bytes_to_long(b'xxxxxx')
p=getPrime(256)
q=getPrime(256)
e=74
n=p*q
c=pow(m,e,n)
print("p=",p)
print("q=",q)
print("c=",c)
#p= 86053582917386343422567174764040471033234388106968488834872953625339458483149
#q= 72031998384560188060716696553519973198388628004850270102102972862328770104493
#c= 3939634105073614197573473825268995321781553470182462454724181094897309933627076266632153551522332244941496491385911139566998817961371516587764621395810123

import binascii

import gmpy2
from gmpy2 import *

p= 86053582917386343422567174764040471033234388106968488834872953625339458483149
q= 72031998384560188060716696553519973198388628004850270102102972862328770104493

phi=(p-1)*(q-1)
e=74
c=3939634105073614197573473825268995321781553470182462454724181094897309933627076266632153551522332244941496491385911139566998817961371516587764621395810123
print(gcd(phi,e))

d=gmpy2.invert(37,phi)

m=pow(c,d,p*q)

ans=gmpy2.iroot(m,2)[0]

print(binascii.unhexlify(hex(ans)[2:]))
#b'LitCTF{e_1s_n0t_@_Prime}'

[LitCTF 2023]隐晦的聊天记录

[LitCTF 2023]easy_math (中级)

from Crypto.Util.number import *
from secret import flag

m = bytes_to_long(flag)
e = 65537
p = getPrime(512)
q = getPrime(128)
n = p*q
hint = p**3-q**5
c = pow(m,e,n)
print(f'n = {n}')
print(f'c = {c}')
print(f'hint = {hint}')
'''
n = 2230791374046346835775433548641067593691369485828070649075162141394476183565187654365131822111419512477883295758461313983481545182887415447403634720326639070667688614534290859200753589300443797
c = 2168563038335029902089976057856861885635845445863841607485310134441400500612435296818745930370268060353437465666224400129105788787423156958336380480503762222278722770240792709450637433509537280
hint = 392490868359411675557103683163021977774935163924606169241731307258226973701652855448542714274348304997416149742779376023311152228735117186027560227613656229190807480010615064372521942836446425717660375242197759811804760170129768647414717571386950790115746414735411766002368288743086845078803312201707960465419405926186622999423245762570917629351110970429987377475979058821154568001902541710817731089463915930932142007312230897818177067675996751110894377356758932
'''

$$\begin{gathered} n=p\ast q \\ hint=p^3-q^5 \end{gathered}$$
构造方程组，z3求解得到p，q后边基本RSA求解。

from z3 import *

x, y = Reals('p q')
hint=392490868359411675557103683163021977774935163924606169241731307258226973701652855448542714274348304997416149742779376023311152228735117186027560227613656229190807480010615064372521942836446425717660375242197759811804760170129768647414717571386950790115746414735411766002368288743086845078803312201707960465419405926186622999423245762570917629351110970429987377475979058821154568001902541710817731089463915930932142007312230897818177067675996751110894377356758932
n=2230791374046346835775433548641067593691369485828070649075162141394476183565187654365131822111419512477883295758461313983481545182887415447403634720326639070667688614534290859200753589300443797


solve(p*q-n == 0, p**3-q**5 == hint)

#[y = 304683618109085947723284393392507415311,
 #x = 7321664971326604351487965655099805117568571010588695608389113791312918573783115429227542573780838065461696504325762281209452761930184231131129306271846427]

from gmpy2 import *
import binascii
p=304683618109085947723284393392507415311
q=7321664971326604351487965655099805117568571010588695608389113791312918573783115429227542573780838065461696504325762281209452761930184231131129306271846427

n=p*q

phi=(p-1)*(q-1)

c=2168563038335029902089976057856861885635845445863841607485310134441400500612435296818745930370268060353437465666224400129105788787423156958336380480503762222278722770240792709450637433509537280

e=65537

d=invert(e,phi)

m=pow(c,d,n)

print(binascii.unhexlify(hex(m)[2:]))

#LitCTF{f9fab7522253e44b48824e914d0801ba}

[LitCTF 2023]我测你vva

考java逆向，不好意思，我确实不会java，但是不耽误做题
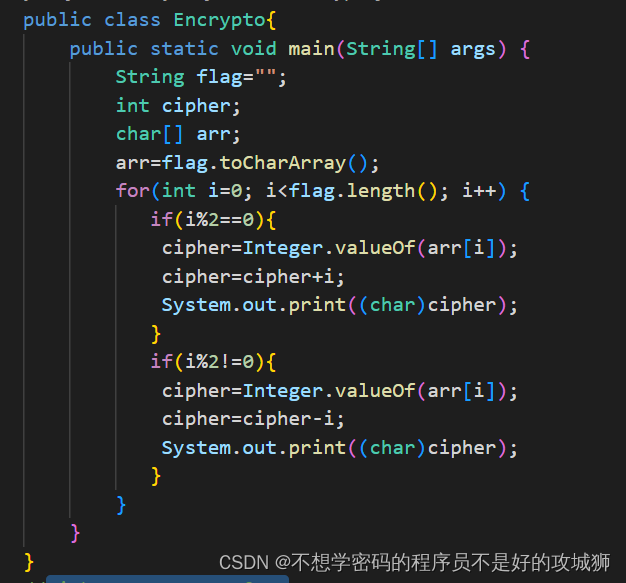不解释了，直接拿py脚本

cipher="HYEQJvPZ~X@+Bp"
cipher=list(cipher)
flag=""
for i in range(len(cipher)):
    if(i%2==0):
        c=ord(cipher[i])-i
        flag+=chr(c)
        #print(chr(c))
    else:
        c=ord(cipher[i])+i
        flag+=chr(c)
        #print(chr(c))

print(flag)

#HZCTF{Java666}

[LitCTF 2023]The same common divisor (高级)

from Crypto.Util.number import *
m=bytes_to_long(b'xxxxxx')
e=65537
p=getPrime(1024)
q1=getPrime(1024)
q2=getPrime(1024)
n1=p*q1
n2=p*q2
c1=pow(m,e,n1)
c2=pow(m,e,n2)
n3=n1^n2
print('n1=',n1)
print('n3=',n3)
print('c1=',c1)
print('c2=',c2)
#n1= 9852079772293301283705208653824307027320071498525390578148444258198605733768947108049676831872672654449631852459503049139275329796717506126689710613873813880735666507857022786447784753088176997374711523987152412069255685005264853118880922539048290400078105858759506186417678959028622484823376958194324034590514104266608644398160457382895380141070373685334979803658172378382884352616985632157233900719194944197689860219335238499593658894630966428723660931647038577670614850305719449893199713589368780231046895222526070730152875112477675102652862254926169713030701937231206405968412044029177246460558028793385980934233
#n3= 4940268030889181135441311597961813780480775970170156650560367030148383674257975796516865571557828263935532335958510269356443566533284856608454193676600884849913964971291145182724888816164723930966472329604608512023988191536173112847915884014445539739070437180314205284883149421228744714989392788108329929896637182055266508625177260492776962915873036873839946591259443753924970795669864031580632650140641456386202636466624658715315856453572441182758855085077441336516178544978457053552156714181607801760605521338788424464551796638531143900048375037218585999440622490119344971822707261432953755569507740550277088437182
#c1= 7066425618980522033304943700150361912772559890076173881522840300333719222157667104461410726444725540513601550570478331917063911791020088865705346188662290524599499769112250751103647749860198318955619903728724860941709527724500004142950768744200491448875522031555564384426372047270359602780292587644737898593450148108629904854675417943165292922990980758572264063039172969633878015560735737699147707712154627358077477591293746136250207139049702201052305840453700782016480965369600667516646007546442708862429431724013679189842300429421340122052682391471347471758814138218632022564279296594279507382548264409296929401260
#c2= 854668035897095127498890630660344701894030345838998465420605524714323454298819946231147930930739944351187708040037822108105697983018529921300277486094149269105712677374751164879455815185393395371001495146490416978221501351569800028842842393448555836910486037183218754013655794027528039329299851644787006463456162952383099752894635657833907958930587328480492546831654755627949756658554724024525108575961076341962292900510328611128404001877137799465932130220386963518903892403159969133882215092783063943679288192557384595152566356483424061922742307738886179947575613661171671781544283180451958232826666741028590085269

有点意思，这里根据
$$\begin{gathered} n_3=n_{1}xor{n}_2 \\ {n}_2=n_{3}xor{n}_1 \end{gathered}$$
这里得到$n_1,n_2$
根据题目提示，首先考虑gcd
验证一下
确实存在公约数，这时可以根据公约是，分解两个大整数。

import binascii

import gmpy2

n1=9852079772293301283705208653824307027320071498525390578148444258198605733768947108049676831872672654449631852459503049139275329796717506126689710613873813880735666507857022786447784753088176997374711523987152412069255685005264853118880922539048290400078105858759506186417678959028622484823376958194324034590514104266608644398160457382895380141070373685334979803658172378382884352616985632157233900719194944197689860219335238499593658894630966428723660931647038577670614850305719449893199713589368780231046895222526070730152875112477675102652862254926169713030701937231206405968412044029177246460558028793385980934233
n3=4940268030889181135441311597961813780480775970170156650560367030148383674257975796516865571557828263935532335958510269356443566533284856608454193676600884849913964971291145182724888816164723930966472329604608512023988191536173112847915884014445539739070437180314205284883149421228744714989392788108329929896637182055266508625177260492776962915873036873839946591259443753924970795669864031580632650140641456386202636466624658715315856453572441182758855085077441336516178544978457053552156714181607801760605521338788424464551796638531143900048375037218585999440622490119344971822707261432953755569507740550277088437182

n2=13275392358603749049507302824073643158313511157306042129424622043169404438475070367199888792522735816696831092853554043588044629442339762181808939836068784930395387656511731023773900700005021564847480224798180592959510217158765133918150651706674329603149481255390797032771700235015269257730220757739489147426447858665350504461218790022992177725157756735193197648927044824616697206813752794351736481372892433605669363455272775767270738838271685683788851792503697508906872616175734362549442203442409947760416740297996886756365560632301306250478012961270642177511142736084877917270911656025730517314096773424314000497639
p=94719927424407179559097379278598331426219665736925758883356208017201441609501349561869578255304543730077703898951251809509592215259248796747648789953238424438984058591393245455685873538467037385791128865102181068065167783963401976811367747317190298098904229431166441000923777869516488107339457633589707290103

q1=n1//p
q2=n2//p

c1=7066425618980522033304943700150361912772559890076173881522840300333719222157667104461410726444725540513601550570478331917063911791020088865705346188662290524599499769112250751103647749860198318955619903728724860941709527724500004142950768744200491448875522031555564384426372047270359602780292587644737898593450148108629904854675417943165292922990980758572264063039172969633878015560735737699147707712154627358077477591293746136250207139049702201052305840453700782016480965369600667516646007546442708862429431724013679189842300429421340122052682391471347471758814138218632022564279296594279507382548264409296929401260
c2=854668035897095127498890630660344701894030345838998465420605524714323454298819946231147930930739944351187708040037822108105697983018529921300277486094149269105712677374751164879455815185393395371001495146490416978221501351569800028842842393448555836910486037183218754013655794027528039329299851644787006463456162952383099752894635657833907958930587328480492546831654755627949756658554724024525108575961076341962292900510328611128404001877137799465932130220386963518903892403159969133882215092783063943679288192557384595152566356483424061922742307738886179947575613661171671781544283180451958232826666741028590085269

e=65537

phi1=(p-1)*(q1-1)
phi2=(p-1)*(q2-1)

d1=gmpy2.invert(e,phi1)
d2=gmpy2.invert(e,phi2)

m1=pow(c1,d1,n1)
m2=pow(c2,d2,n2)

print(binascii.unhexlify(hex(m1)[2:]))
print(binascii.unhexlify(hex(m2)[2:]))

#b'LitCTF{TH3_Tw0_nUmb3rs_H@v3_The_sAme_D1v1s0r!!}'
#b'LitCTF{TH3_Tw0_nUmb3rs_H@v3_The_sAme_D1v1s0r!!}'

没注意看，以为是分段的flag需要求解两个。

[LitCTF 2023]Euler

from Crypto.Util.number import *
from secret import flag

m = bytes_to_long(flag)
p = getPrime(512)
q = getPrime(512)
n = p*q
c = pow(m,n-p-q+3,n)
print(f'n = {n}')
print(f'c = {c}')
"""
n = 115140122725890943990475192890188343698762004010330526468754961357872096040956340092062274481843042907652320664917728267982409212988849109825729150839069369465433531269728824368749655421846730162477193420534803525810831025762500375845466064264837531992986534097821734242082950392892529951104643690838773406549
c = 406480424882876909664869928877322864482740577681292497936198951316587691545267772748204383995815523935005725558478033908575228532559165174398668885819826720515607326399097899572022020453298441
"""

根据题目提示，本题考查欧拉定理
$$m^{n-p-q+3}=m^{(p-1)\ast (q-1)+2}=m^{phi+2}modn$$
根据欧拉定理
$$m^{phi+2}modn=m^{2}modn$$
因此，对c开根号就能解密。

import binascii

import gmpy2

c=406480424882876909664869928877322864482740577681292497936198951316587691545267772748204383995815523935005725558478033908575228532559165174398668885819826720515607326399097899572022020453298441

m=gmpy2.iroot(c,2)[0]

print(binascii.unhexlify(hex(m)[2:]))
#b'LitCTF{a1a8887793acfc199182a649e905daab}'

[LitCTF 2023]Virginia

这个题目也不错，挺有意思。

Uwegxp skso tnnd mkxdamj eo zmzsk upovqp wnt xegs dosjehosr tu dzu,zt ehuxp wnt sabj eoahsej dzux qtfk ny otj hae tc attehkw,eo zmzsk bso sfve etf ssnwe cmpn etf rkfwle spej ne,tu ysoyj ehgy xaqj joa xpe zmp bxnrhzjc soip ol ysitld wnjy yuz lrk wparqj duby,tu ysoyj hhu dzu cfyt zt wez yses pyoc ysaz dzu guarkhtazj ehknc fxnpnjxsiv.Fyd ok joa izn’z, izn’z bzrxd,yozmtnm gld cnwl nfapks eo etf,yuz hirq uuyy xiyx zuz ty tnj zpvtctastte yz bxnrhzjy surpotj’d dgd hizm ehox xeyxlgk.Rj pgxdwuwo iy szt g wpgaqlr Ifpsgw aayxhoxi,lnj yse ksn frfr

用维吉尼亚爆破第二段密文，提示说后边的列表不是一个简单的凯撒

a=[86, 116, 128, 80, 98, 85, 139, 122, 134, 114, 125, 136, 117, 123, 129, 127, 128, 128, 142, 130, 140, 147, 127, 132, 131, 136, 151, 134, 152, 164]

flag=""
b="LitCTF"
cnt=10
for i in range(len(a)):
    print(a[i]-cnt)
    flag+=chr(a[i]-cnt)
    cnt+=1

print(flag)
#LitCTF{it_is_different_caesar}