实验三主要使用FEM和hyperelastic模型完成弹性体的模拟

完整项目已上传至github。

---

Linear finite element method(FEM)

弹性的力永远都是想阻碍形变的(划重点)。有限元方法(Finite Element Method) 把物体分割成一个个有体积的单元来模拟。例如，线性有限元方法在二维空间中把物体分割成三角形，在三维空间中把物体分割成四面体。

下面以二维空间上的有限元方法为例

二维空间有限元方法

如下图所示，我们把三角形静止时(未发生形变)的状态称为 Reference 状态。假设三角形内部的形变是均匀的，三角形内任意点 $\vec{X}$ 形变以后的位置 $\vec{x}=\vec{F}\vec{X}+\vec{c}$。注意大写表示形变之前的状态，小写表示形变之后的状态。

则任意向量 ${\vec{X}}_{ba}$ 形变后变成 ${\vec{x}}_{ba}=\vec{F}{\vec{X}}_{ba}$。

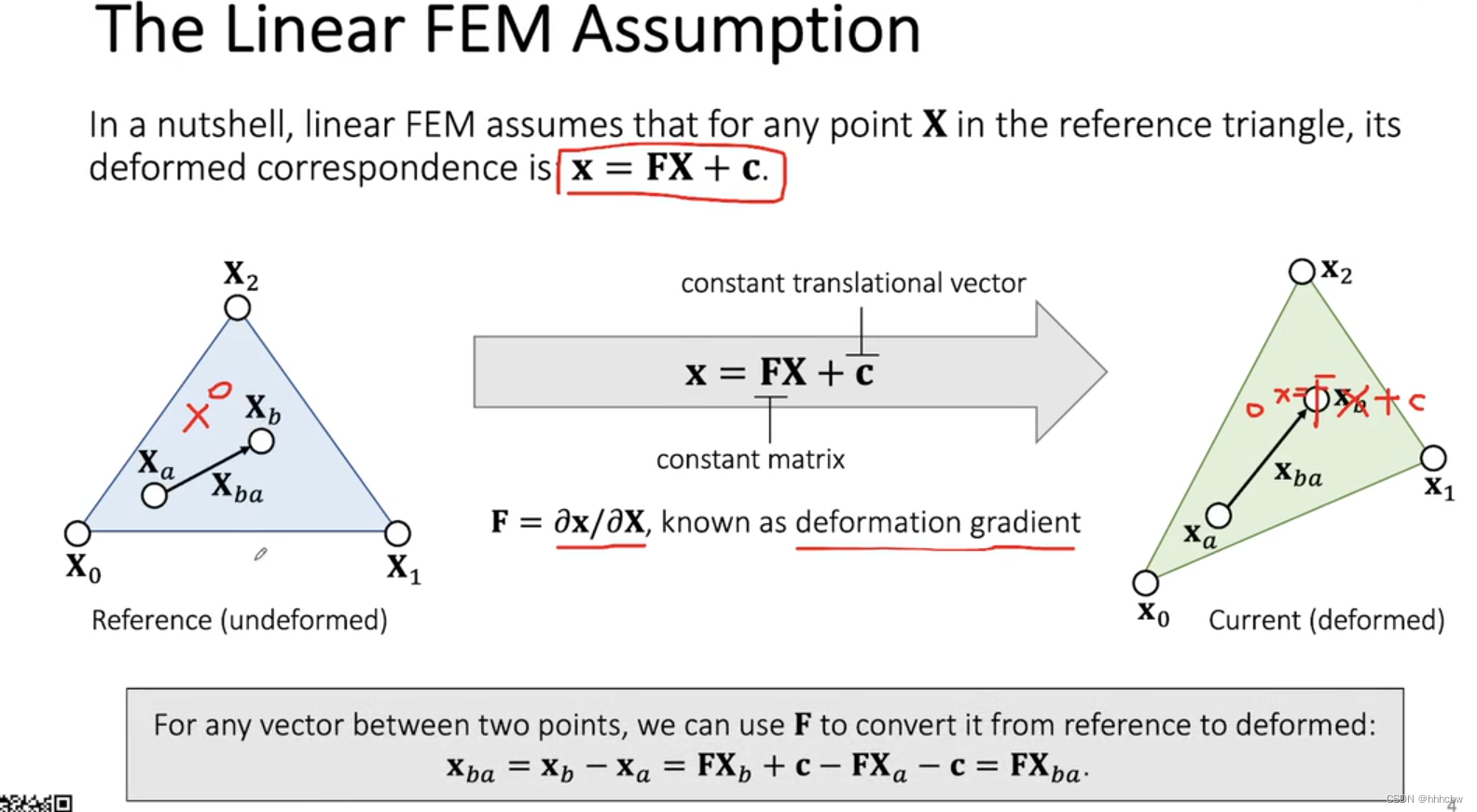
变形梯度(Deformation Gradient)

因为是二维情况(力有两个未知项)，所以需要用形变前后三角形两个边向量就能求出 $\vec{F}=[{\vec{x}}_{10}{\vec{x}}_{20}][{\vec{X}}_{10}{\vec{X}}_{20}{]}^{-1}$。但是求出的力还包括了与旋转相关的部分。

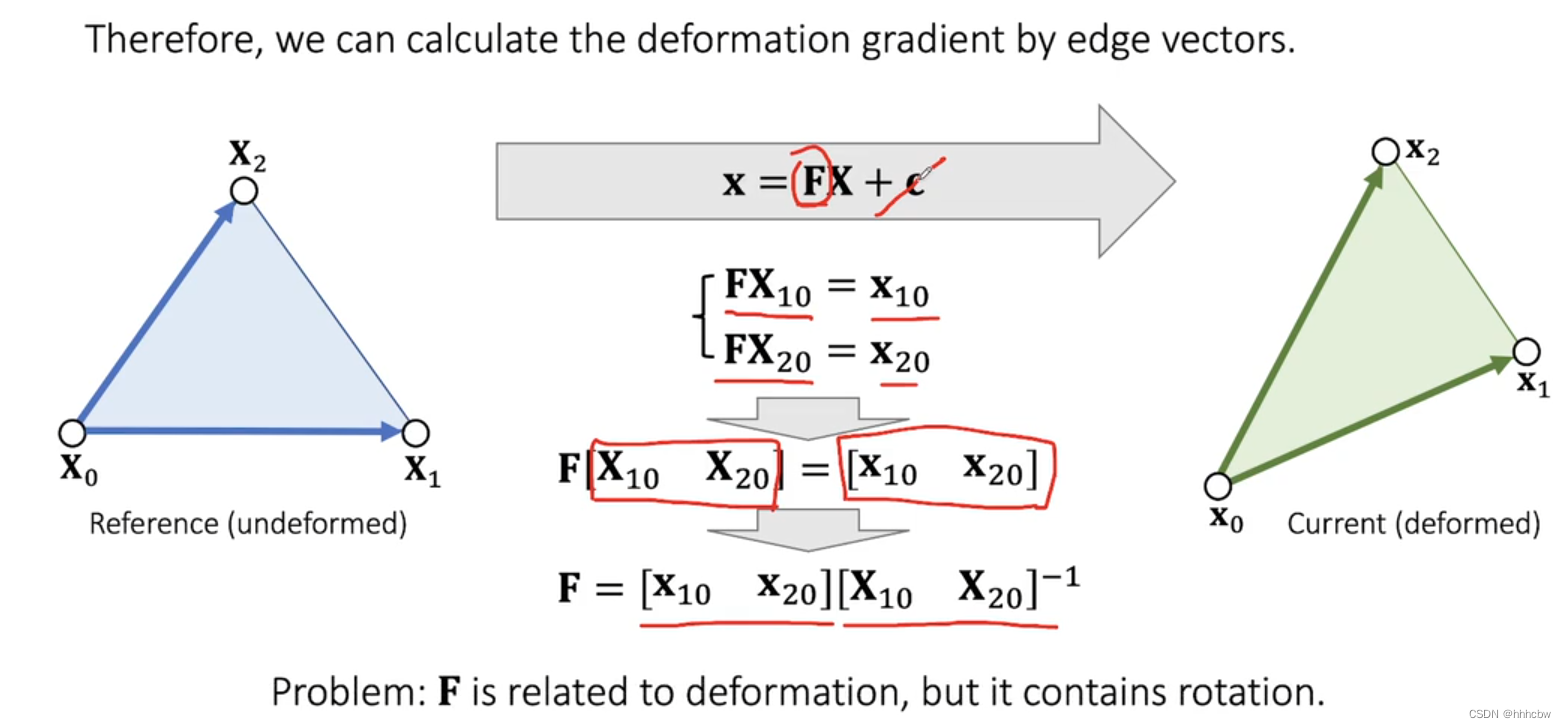
格林应变(Green Strain)

我们可以使用SVD(前两个部分与形变有关，最后一个与旋转有关)分解，求出仅与形变有关的部分。但做SVD分解太复杂了，这里引入 Green Strain，其与旋转无关，仅描述形变(就是做一些矩阵运算，消去旋转部分)。

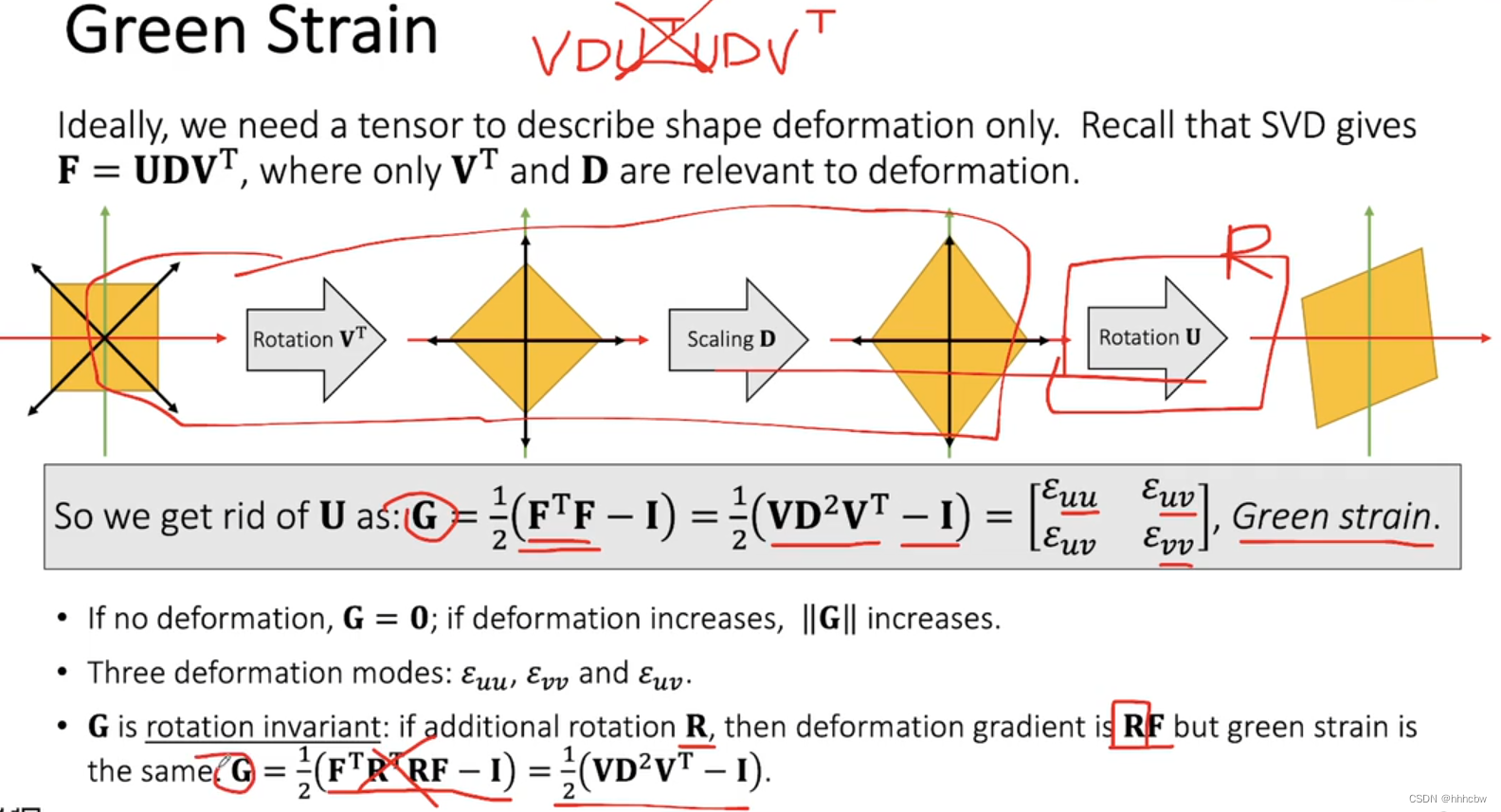
应变能量密度函数(Strain Energy Density Function)

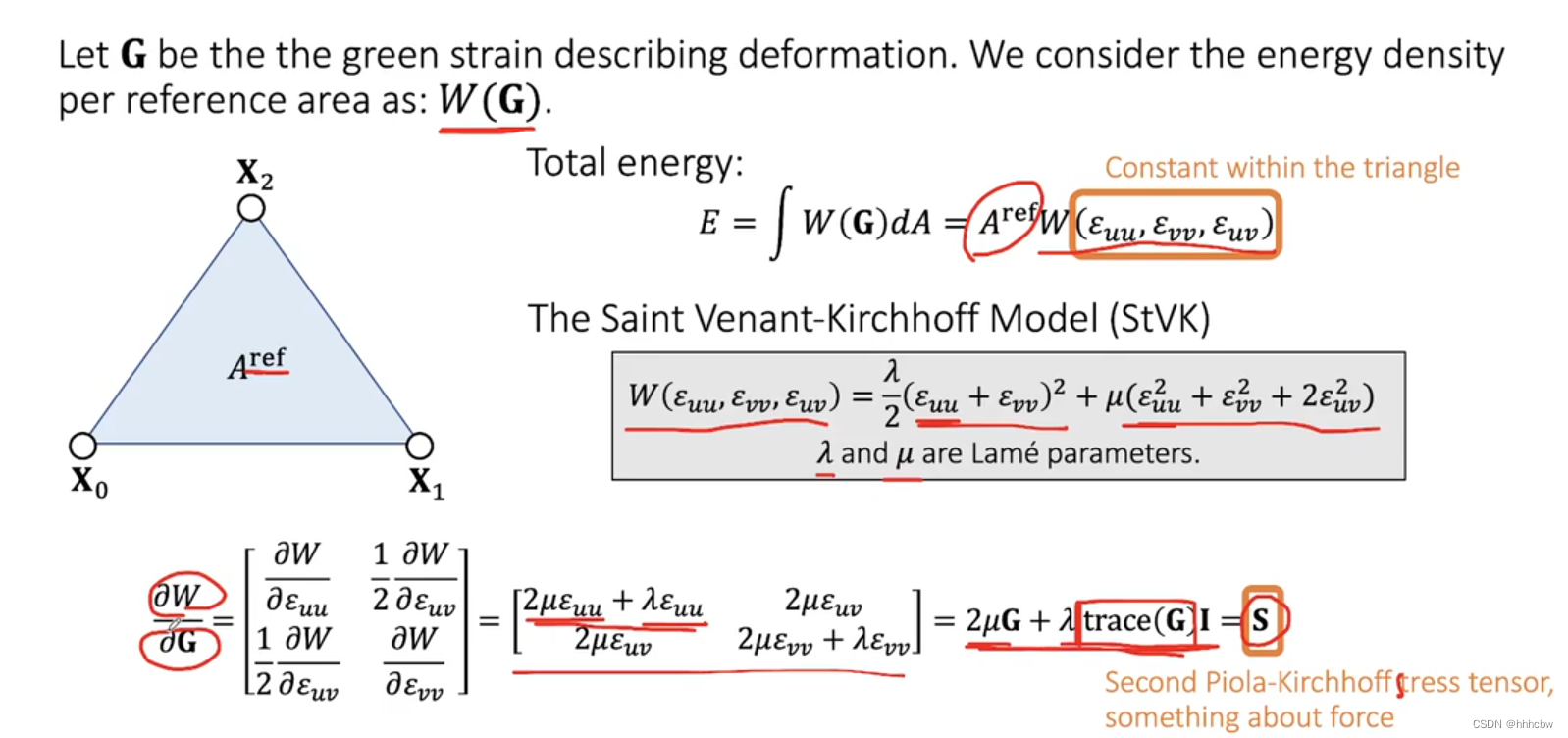
我们再引入一个新的量 $W(\vec{G})$ 描述参考区域的能量密度。由于在三角形内量，能量密度是常量，总能量就是 $W(\vec{G})\ast dA$ 在参考域上的积分。$W(\vec{G})$ 直接决定了材料的性质，这里使用StVK模型。

这里最后的 $2\mu +\lambda trace(\vec{G}I)=S$ 适用于任意维度。这里都是相对静止状态的，所以这里就得到第二皮奥拉-基尔霍夫应力(Second Piola-Krichhoff Stress Tensor)

力(Force)

有了能量的定义，力就可以由能量关于位矢求偏导取负号得到了。

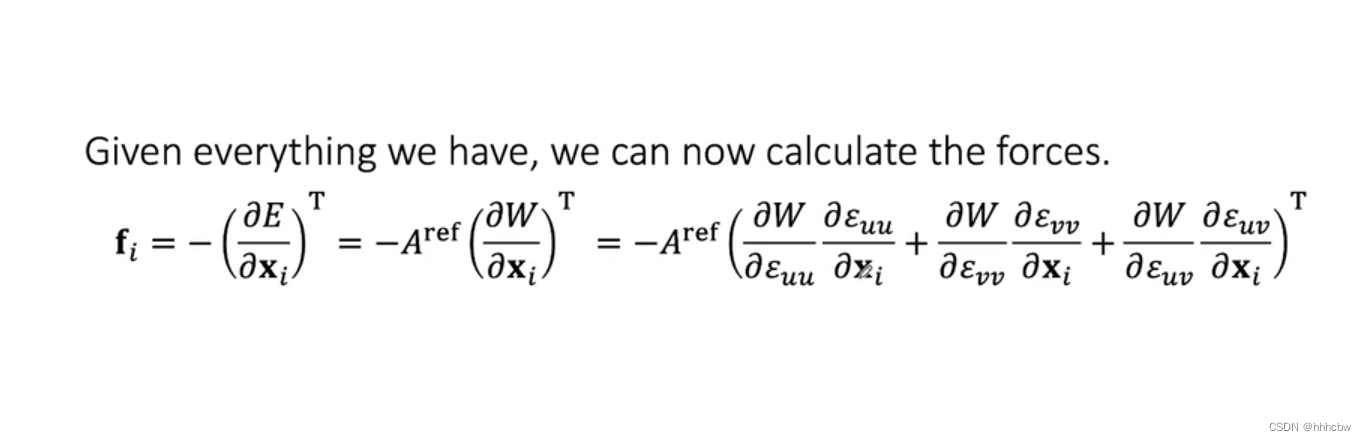
由之前关于 $\vec{F}$ 和 $\vec{G}$ 的公式，代入可以最后得到 ${\vec{f}}_1$ 关于$A^{ref}$，$F$，$S$的表示。


${\vec{f}}_2$ 也同理能求得，而由系统内合力为 0，我们也可以求得 ${\vec{f}}_0$

---

Finite Volume Method(FVM)

FVM 从有限体积的角度考虑，其实对于简单的线性的三角形或四面体，这两个方法是等价的。

Traction and Stress

基于力是从何而来的思想；定义一个 traction 表示单位长度(面积)上的力，那么表面上的全部力就是 traction 在表面上的积分，而 traction 是与应力张量和法向量有关

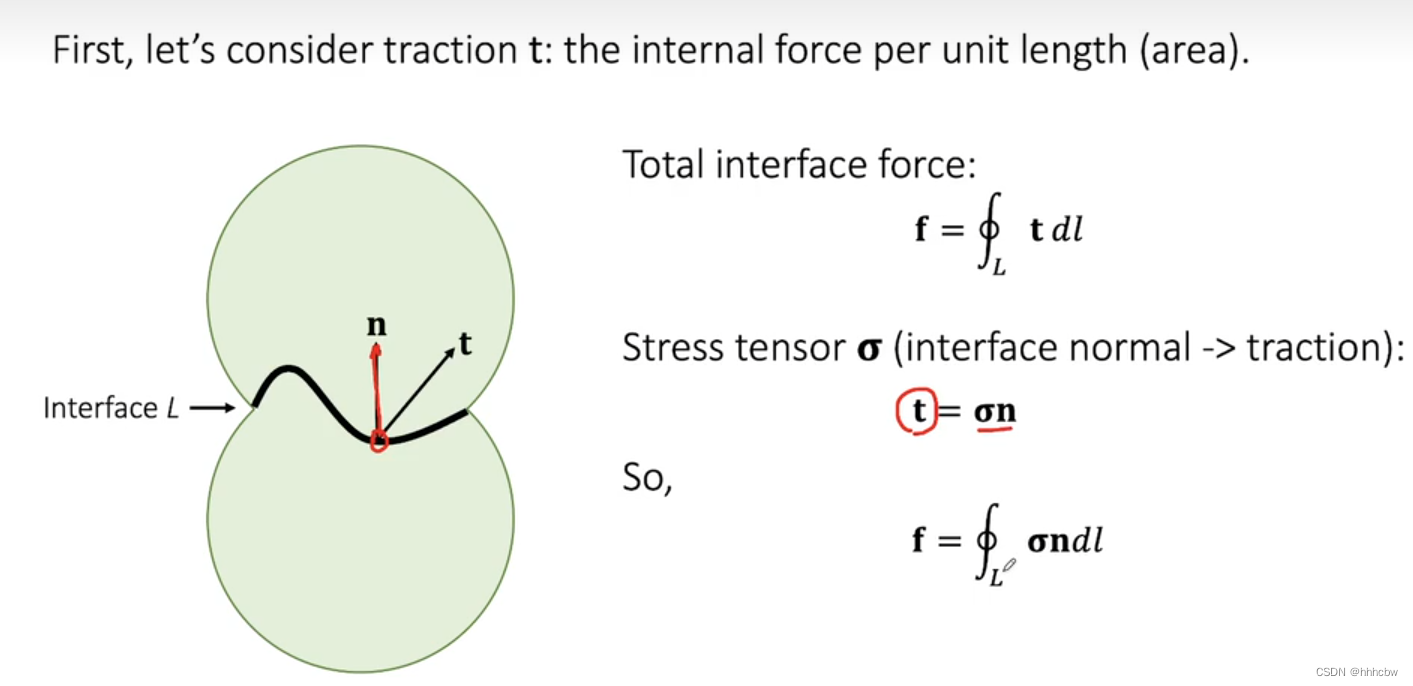
The Finite Volume Method

相当于对法向量进行积分，而在封闭曲线上对法向量积分结果为 0。取中点是为了对三个点力的共享是均匀的。

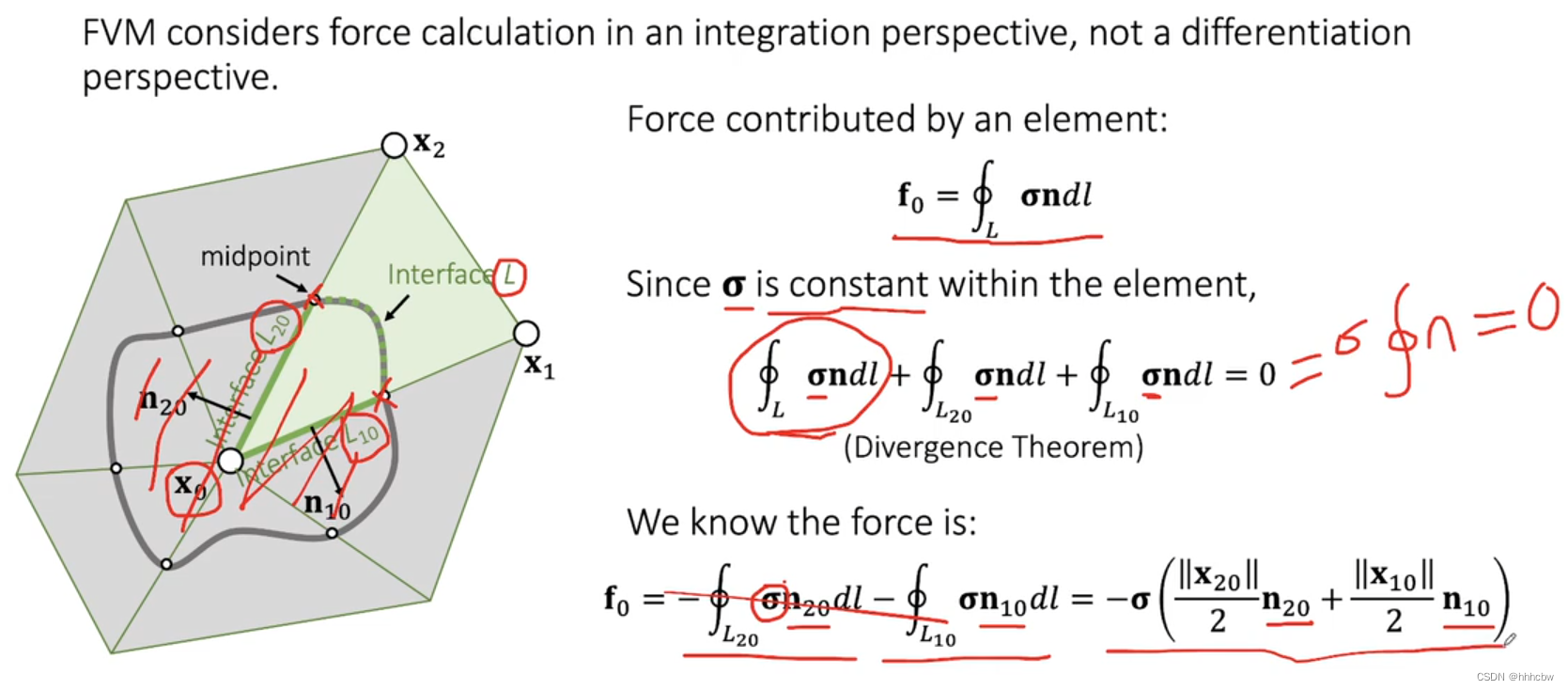
三维的情况就是面积分了

不同参考状态下的stress

在FEM中，能量密度 W 是在参考状态下定义的。因此，应力 S 是一个将参考状态的法向量 $\vec{N}$ 映射到参考状态的 traction $\vec{T}$。而在FVM中，则是在形变状态下的映射。

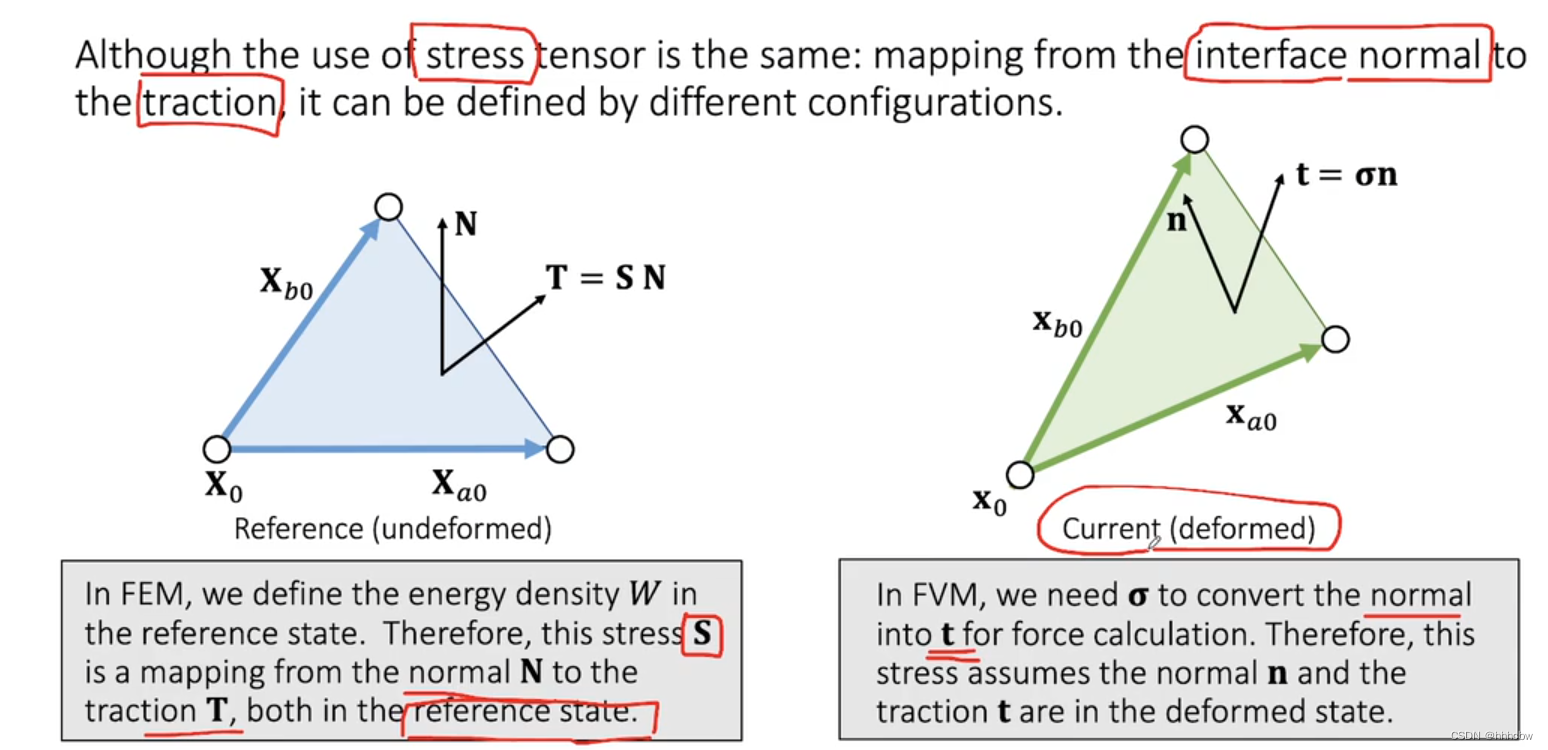
这些应力实际是等价的，只不过参考的状态不同。我们可以由Second Piola-Kirchhoff stress乘上 F 得到 First Piola-Kirchoff stress。再由 First Piola-Kirchoff stress得到Cauchy stress。

下面我们根据两个状态下 Area Weighted Normals 之间的关系，找到 First Piola-Kirchhoff stress 与 Cauchy Stress 之间的关系


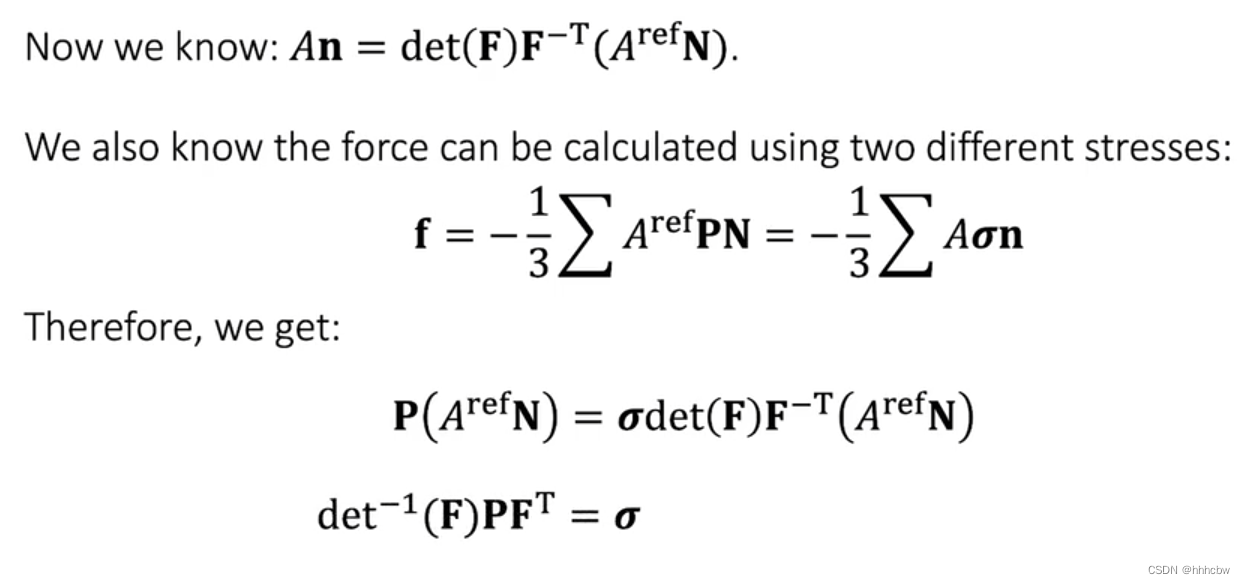
我们得到不同状态下应力之间的关系

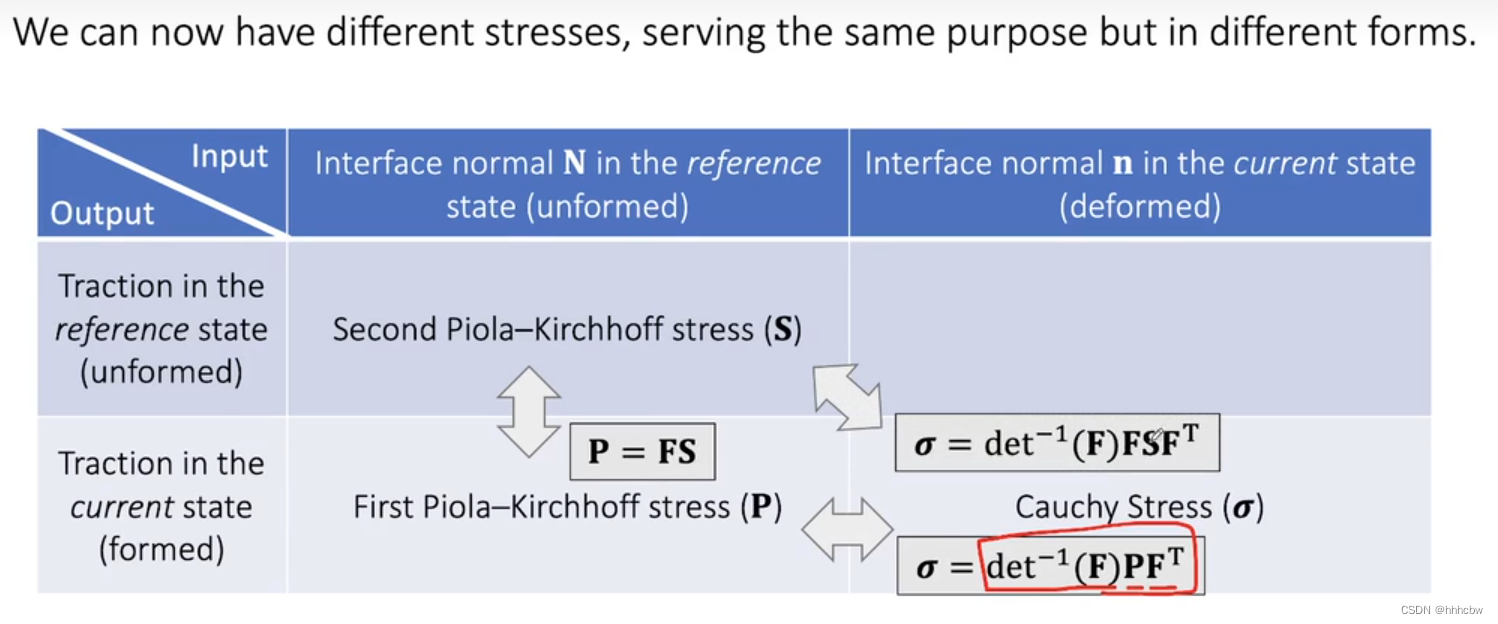
有了上面应力之间的转换关系，我们可以把之前形变状态下的公式，转化一下，因为后面叉乘求和是个常量，因此可用提前计算得到。

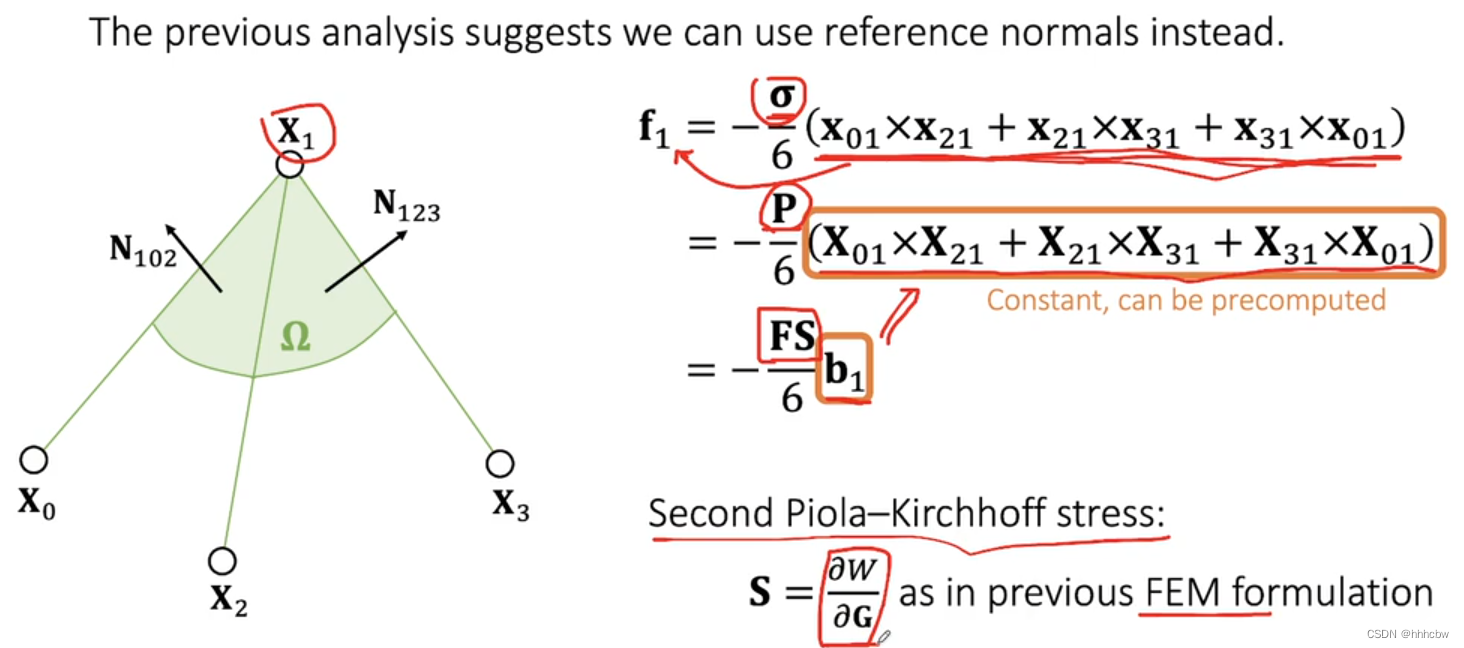
后续可以进一步化简，比如 $X_{10}$ 与 $X_{01}\times X_{21}$ 的点乘结果肯定是 0，因为叉乘产生的向量垂直于 $X_{10}$。
由 $\frac{1}{det([{\vec{X}}_{10}{\vec{X}}_{20}{\vec{X}}_{30}{]}^{-1})}=det[{\vec{X}}_{10}{\vec{X}}_{20}{\vec{X}}_{30}]$ 可进一步得到如下公式

算法流程

根据上面的推导，可以总结为如下算法流程

代码

核心代码如下，就是按照上面的算法流程，把对应的物理量计算出来，带入公式即可。这里由于是显式积分，所以存在数值不稳定性，使用拉普拉斯平滑进行处理(就是加权平均一个体的其他三个点的速度)

    	for(int tet=0; tet<tet_number; tet++)
    	{
            //TODO: Deformation Gradient
            Matrix4x4 F = Build_Edge_Matrix(tet) * inv_Dm[tet];
            //TODO: Green Strain
            Matrix4x4 G = Matrix4x4_mul_float(Matrix4x4_minus_Matrix4x4(F.transpose * F, Matrix4x4.identity), 0.5f);
            //TODO: Second PK Stress
            Matrix4x4 S = Matrix4x4.zero;
            float trace = G[0, 0] + G[1, 1] + G[2, 2];
            S = Matrix4x4_add_Matrix4x4(Matrix4x4_mul_float(G, 2.0f * stiffness_1), Matrix4x4_mul_float(Matrix4x4.identity, stiffness_0 * trace));
            //TODO: Elastic Force
            float volume = 1.0f / (inv_Dm[tet].determinant * 6);
            Matrix4x4 Elastic_force = Matrix4x4_mul_float(F * S * inv_Dm[tet].transpose, -volume);
            for (int k=0; k<3; k++)
            {
                Force[Tet[tet * 4 + k + 1]].x += Elastic_force[0, k];
                Force[Tet[tet * 4 + k + 1]].y += Elastic_force[1, k];
                Force[Tet[tet * 4 + k + 1]].z += Elastic_force[2, k];
            }

            // Elastic_force0 = -Elastic_force1-Elastic_force2-Elastic_force3
            Force[Tet[tet * 4 + 0]].x -= Elastic_force[0, 0] + Elastic_force[0, 1] + Elastic_force[0, 2];
            Force[Tet[tet * 4 + 0]].y -= Elastic_force[1, 0] + Elastic_force[1, 1] + Elastic_force[1, 2];
            Force[Tet[tet * 4 + 0]].z -= Elastic_force[2, 0] + Elastic_force[2, 1] + Elastic_force[2, 2];
        }

        Smooth_V(0.75f);

结果

---

Hyperelastic Models

Isotropic Materials

各向同性材料，其与拉伸方向无关。P可以认为是F的一个函数，Principal stretches是对角元素，表示三个方向上的拉伸量

在论文中，一般以下面的方式表示，PPT里把$I{I}_C$与$II{I}_C$写反了。

论文里的如下

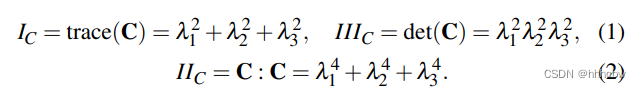
Isotropic Models

第一项抵抗拉伸，第二项阻止体积改变

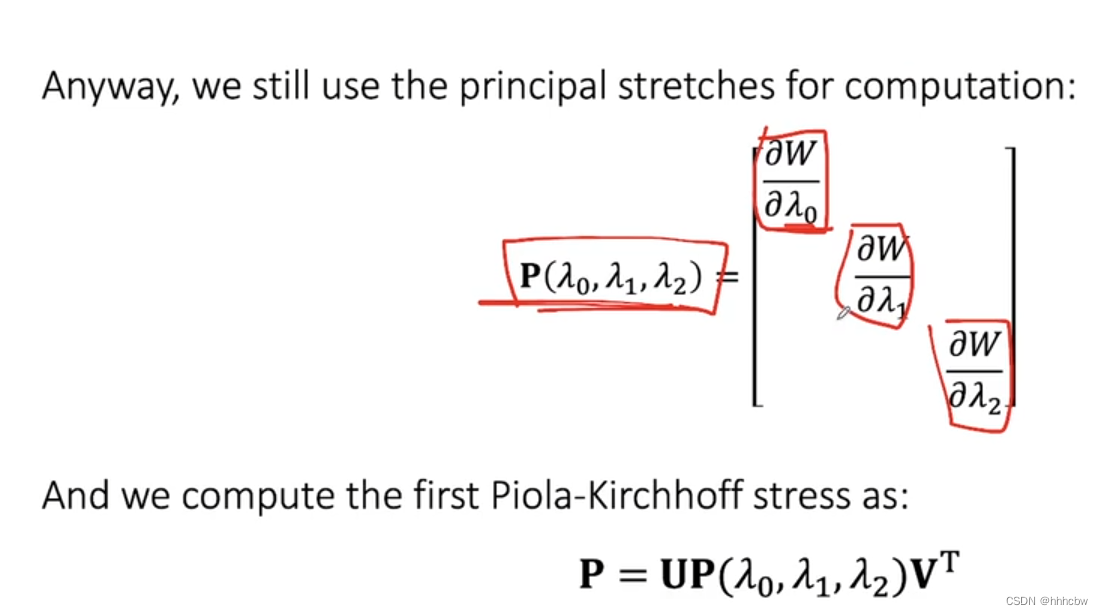
算法流程

这里就是使用SVD分解F，利用上面公式计算 P，这里可以替换不同的 W 以更换不同的模型

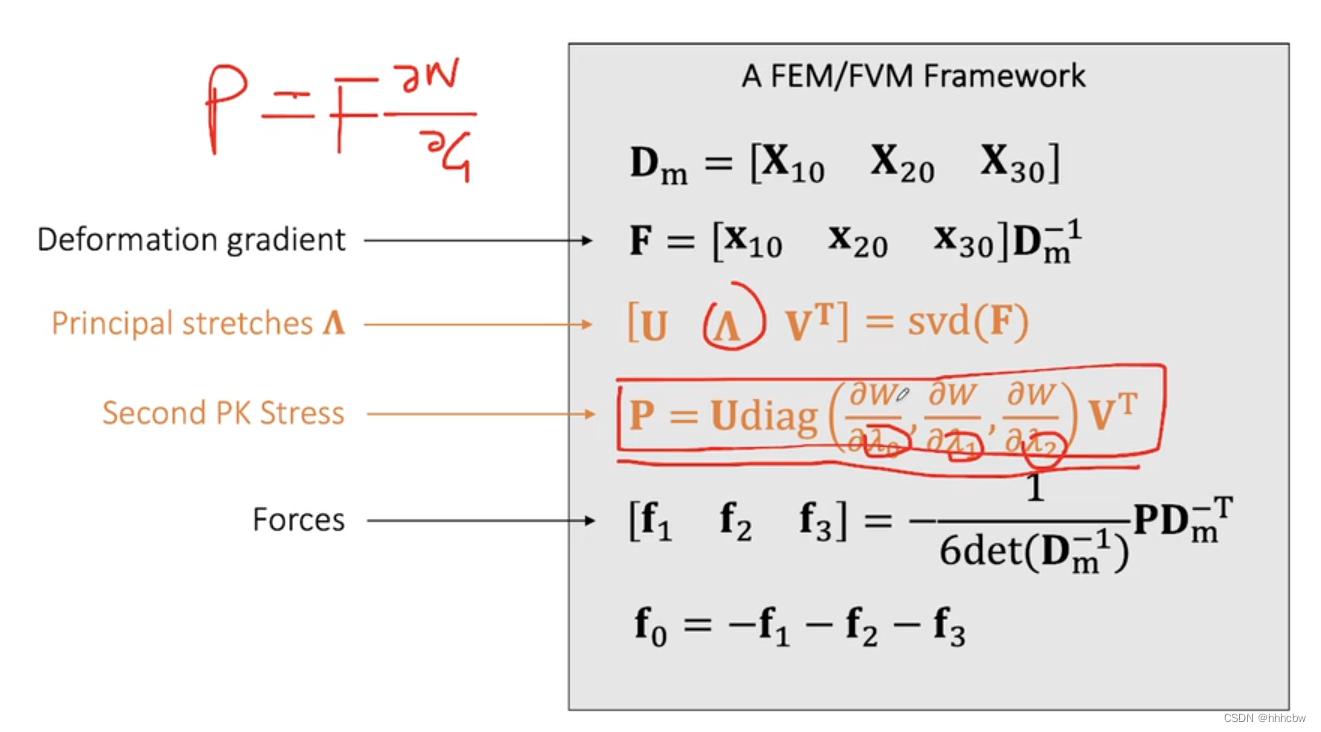
代码

W 对 $\lambda$ 求偏导结果如下

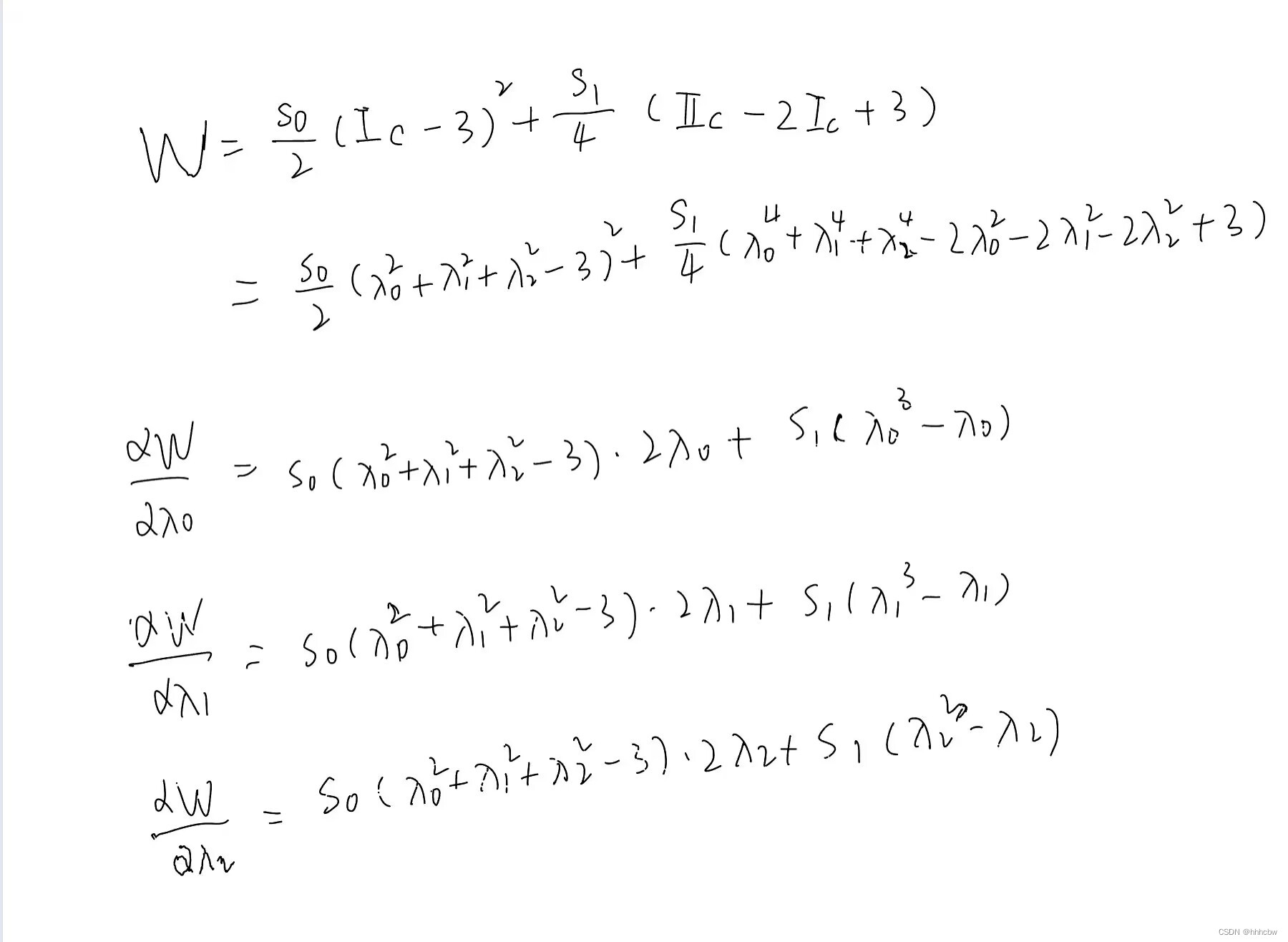
核心代码如下，在前面需要把 stiffness_0 改为 5000.0f

        // Hyperelastic Models
        for (int tet = 0; tet < tet_number; tet++)
        {
            //TODO: Deformation Gradient
            Matrix4x4 F = Build_Edge_Matrix(tet) * inv_Dm[tet];
            F[3, 3] = 1.0f;
            //TODO: Green Strain
            Matrix4x4 U = new Matrix4x4();
            Matrix4x4 S = new Matrix4x4();
            Matrix4x4 V = new Matrix4x4();
            svd.svd(F, ref U, ref S, ref V);
            //TODO: First PK Stress
            Matrix4x4 P = new Matrix4x4();
            Matrix4x4 Diag = new Matrix4x4();
            float sum2 = S[0, 0] * S[0, 0] + S[1, 1] * S[1, 1] + S[2, 2] * S[2, 2] - 3.0f;
            Diag[0, 0] = stiffness_0 * sum2 * 2.0f * S[0, 0] + stiffness_1 * (S[0, 0] * S[0, 0] * S[0, 0] - S[0, 0]);
            Diag[1, 1] = stiffness_0 * sum2 * 2.0f * S[1, 1] + stiffness_1 * (S[1, 1] * S[1, 1] * S[1, 1] - S[1, 1]);
            Diag[2, 2] = stiffness_0 * sum2 * 2.0f * S[2, 2] + stiffness_1 * (S[2, 2] * S[2, 2] * S[2, 2] - S[2, 2]);
            U[3, 3] = Diag[3, 3] = V[3, 3] = 1.0f;
            P = U * Diag * V.transpose;
            //TODO: Elastic Force
            float volume = 1.0f / (inv_Dm[tet].determinant * 6);
            Matrix4x4 Elastic_force = Matrix4x4_mul_float(P * inv_Dm[tet].transpose, -volume);
            for (int k = 0; k < 3; k++)
            {
                Force[Tet[tet * 4 + k + 1]].x += Elastic_force[0, k];
                Force[Tet[tet * 4 + k + 1]].y += Elastic_force[1, k];
                Force[Tet[tet * 4 + k + 1]].z += Elastic_force[2, k];
            }

            // Elastic_force0 = -Elastic_force1-Elastic_force2-Elastic_force3
            Force[Tet[tet * 4 + 0]].x -= Elastic_force[0, 0] + Elastic_force[0, 1] + Elastic_force[0, 2];
            Force[Tet[tet * 4 + 0]].y -= Elastic_force[1, 0] + Elastic_force[1, 1] + Elastic_force[1, 2];
            Force[Tet[tet * 4 + 0]].z -= Elastic_force[2, 0] + Elastic_force[2, 1] + Elastic_force[2, 2];
        }

结果

因为使用了 SVD，导致仿真速度变慢