双指针
- 同向双指针
- 3. 无重复字符的最长子串
- 209. 长度最小的子数组
- 713. 乘积小于 K 的子数组
- 相向双指针
- 167. 两数之和 II - 输入有序数组
- 15. 三数之和
- 438. 找到字符串中所有字母异位词
- 滑动窗口
- 接雨水
同向双指针
3. 无重复字符的最长子串
题目链接
class Solution {
public:
int lengthOfLongestSubstring(string s) {
int ret=0;
unordered_map<char,int> hashmap;
for(int i=0,j=0;j<s.size();j++)
{
hashmap[s[j]]++;
while(hashmap[s[j]]>1)//当当前字符的哈希值大于1,说明前面有重复的,
//要删除,在while里删除,从i位置开始删,直到,当前值的哈希不大于1,删的过程也会把其他字符的哈希--,那是应该的,因为题目要求的是连续不重复子串
{
hashmap[s[i]]--;
i++;
}
ret=max(ret,j-i+1);
}
return ret;
}
};
“\n”
209. 长度最小的子数组

题目链接
class Solution {
public:
int minSubArrayLen(int target, vector<int>& nums) {
int n=nums.size();
int minsize=n+1;
int sum=0;
for(int i=0,j=0;j<n;j++)//用j进行遍历加
{
sum+=nums[j];
while(sum>=target)//在while里面不断进行sum减少,让其不满足while,同时指针i向后移动
{
minsize=min(minsize,j-i+1);
sum-=nums[i];
i++;
}
}
return minsize > n ? 0 : minsize;
}
};
“\n”
713. 乘积小于 K 的子数组

题目链接
class Solution {
public:
int numSubarrayProductLessThanK(vector<int>& nums, int k) {
if(k<=1)
return 0;
int num=0;
int mult=1;
for(int j=0,i=0;j<nums.size();j++)
{
mult*=nums[j];
while(mult>=k)
{
mult/=nums[i];
i++;
}
num+=j-i+1;
//求和 使用符合条件的区间内元素个数
}
return num;
}
};
这三道题都是双指针解决,基本都是一个模子,外循环遍历结点,内循环while判断区间条件,最后出while对区间长度计算,返回结果
相向双指针
167. 两数之和 II - 输入有序数组

题目链接
这个题还行,能够理解,一有思路就能写出来
class Solution {
public:
//相向双指针:不断缩减区间,每一次都能缩减一个元素
vector<int> twoSum(vector<int>& numbers, int target) {
int n=numbers.size();
vector<int> ret(2);
for(int i=0,j=n-1;i<j;)
{
//要很好的利用到数组升序这个条件,如果不升序,那就将其变为升序,保存原先的下标
if(numbers[i]+numbers[j]>target)
{j--;continue;}
if(numbers[i]+numbers[j]<target)
{i++;continue;}
//每次花O(1)时间去删除一个元素,减少元素的个数
//原先花费O(n)的时间,获取O(1)的信息,即:遍历一遍,只能直到一个数与其他数组合不行
//现在花费O(1)的时间,获取O(n)的信息,即:知道这个数,和任何其他数都不能组成,直接把区间缩小了
else
{
ret[0]=i+1;
ret[1]=j+1;
return ret;
}
}
return ret;
}
};
// class Solution {
// public:
// vector<int> twoSum(vector<int>& numbers, int target) {
// int n=numbers.size();
// vector<int> ret(2);
// for(int i=0;i<n-1;i++)
// {
// if(i!=0&&numbers[i]!=0&&numbers[i]==numbers[i-1])continue;
// for(int j=i+1;j<n;j++)
// {
// if(numbers[j]!=0&&numbers[j]==numbers[j-1])continue;
// if(numbers[i]+numbers[j]==target)
// {
// ret[0]=i+1;
// ret[1]=j+1;
// return ret;
// }
// else if(numbers[i]+numbers[j]>target)
// break;
// }
// }
// return ret;
// }
// };
15. 三数之和
题目链接
能看懂思路,但是写不出来,特判好多,以及何时就应该移动指针。没有想到转换成两数求和
class Solution{
public:
vector<vector<int>> threeSum(vector<int>& nums)
{
int size = nums.size();
if (size < 3) return {}; // 特判
vector<vector<int> >res; // 保存结果(所有不重复的三元组)
std::sort(nums.begin(), nums.end());// 排序(默认递增)
for (int i = 0; i < size; i++) // 固定第一个数,转化为求两数之和
{
if (nums[i] > 0) return res; // 第一个数大于 0,后面都是递增正数,不可能相加为零了
// 去重:如果此数已经选取过,跳过
if (i > 0 && nums[i] == nums[i-1]) continue;
// 双指针在nums[i]后面的区间中寻找和为0-nums[i]的另外两个数
int left = i + 1;
int right = size - 1;
while (left < right)
{
if (nums[left] + nums[right] > -nums[i])
right--; // 两数之和太大,右指针左移
else if (nums[left] + nums[right] < -nums[i])
left++; // 两数之和太小,左指针右移
else
{
// 找到一个和为零的三元组,添加到结果中,左右指针内缩,继续寻找
res.push_back(vector<int>{nums[i], nums[left], nums[right]});
left++;
right--;
// 去重:第二个数和第三个数也不重复选取
// 例如:[-4,1,1,1,2,3,3,3], i=0, left=1, right=5
while (left < right && nums[left] == nums[left-1]) left++;
while (left < right && nums[right] == nums[right+1]) right--;
}
}
}
return res;
}
};
我的想法:排序,先找0,然后从0位置向前向后遍历,找相加=0,之后找一个正数的情况,和一个负数的情况,注意当区间之和大于0或小于0时,剩下的元素就不用判断了,没写完
class Solution {
public:
//至少有一个负数,除非全是0
//可能有一个正数或两个,一个正数,也可能有0
//总结起来:1.有0;2.一个正;3.一个负
vector<vector<int>> threeSum(vector<int>& nums) {
int n=nums.size();
vector<vector<int>> arr;
vector<int> temp{0,0,0};
sort(nums.begin(),nums.end());
int cnt=0;
for(int i=0;i<n;i++)
{
if(0==nums[i])cnt++;
if(cnt==3)break;
}
if(cnt==3)
arr.push_back(temp);
int zero_pos=-1;
for(int i=0;i<n;i++)
{
if(nums[i]==0)
{zero_pos=i;break;}
}
//0存在,找到0的位置了
if(zero_pos!=-1)
{
int left=zero_pos,right=zero_pos;
while(left>=0&&right<n)
{
for()
}
}
// vector<pair<int,int>> hash;
// int i=0;
// for(auto& x:hash)
// {
// x.first=nums[i++];
// x.second=i;
// }
// sort(hash.begin(),hash.end(),[](const pair<int,int>& p1,const pair<int,int>& p2)
// {return p1.first>p2.first;});
}
};
438. 找到字符串中所有字母异位词
题目链接
一种经典思路是初始化p的字符数组然后维护数组每个元素不小于0。 开始向右滑动窗口,减去并相应字符,
如果频率小于0就收缩左侧边界直到频率不再小于0。窗口长度与p长度一致时达成条件。
vector<int> findAnagrams(string s,string p)
{
int m=s.size();
int n=p.size();
if(m<n)return {};
vector<int> hs(26);
for(auto x:p)
++hs[x-'a'];
vector<int> ret;
for(int l=0,r=0;r<m;r++)//滑动窗口为:[l,r],初始窗口为[0,0]
{
--hs[s[r]-'a'];
while(hs[s[r]-'a']<0)//有某一字符的hash为负数,说明此时新加入字符,造成窗口[l,r]内的子串,是不符合p的,因为小于说明某一字符是多的,那么就要while重新调整子串
{
++hs[s[l]-'a'];
++l;
//调整子串从left开始,到right,会越界吗,不会,因为即便是最总也就是窗口内没有字符了,无需越界判断
}
if(r-l+1==n)//当窗口大小和p的长度一样,能走到这一步说明,元素组成是相同的,顺序不关心,把left加入ret
ret.push_back(l);
}
return ret;
}
这一题虽说是滑动窗口,但其实和双指针差不多,可以看到的是在核心的代码也是for遍历内部加while判断
滑动窗口
接雨水

题目链接
方法一:
//方法一:
//求每一个位置的前缀pre最大,和后缀tail最大
//每一处能存水的多少,就是min(pre,tail)-height[i]要减去当前的柱子高度
int trap(vector<int>& height) {
int n=height.size();
vector<int> pre_arr(n);
vector<int> tail_arr(n);
pre_arr[0]=height[0];
tail_arr[n-1]=height[n-1];
for(int i=1,j=n-2;i<n;i++,j--)
{
pre_arr[i]=max(pre_arr[i-1],height[i]);
tail_arr[j]=max(height[j],tail_arr[j+1]);
}
int sum=0;
for(int i=0;i<n;i++)
{
sum+=(min(pre_arr[i],tail_arr[i])-height[i]);
}
return sum;
}
方法二:
//方法2:
int trap(vector<int>& height)
{
int left=0;
int max_left=height[left];
int right=height.size()-1;
int max_right=height[right];
int sum=0;
while(left<right)
{
//如果左最大 < 右最大,此时肯定是依照左来计算,因为右边即便有更大的,雨水也不会接高于左
if(max_left<=max_right)
{
sum+=max_left-height[left];
left++;
max_left=max(max_left,height[left]);
}
//右侧同理
else
{
sum+=max_right-height[right];
right--;
max_right=max(max_right,height[right]);
}
}
return sum;
}
- 盛最多水的容器
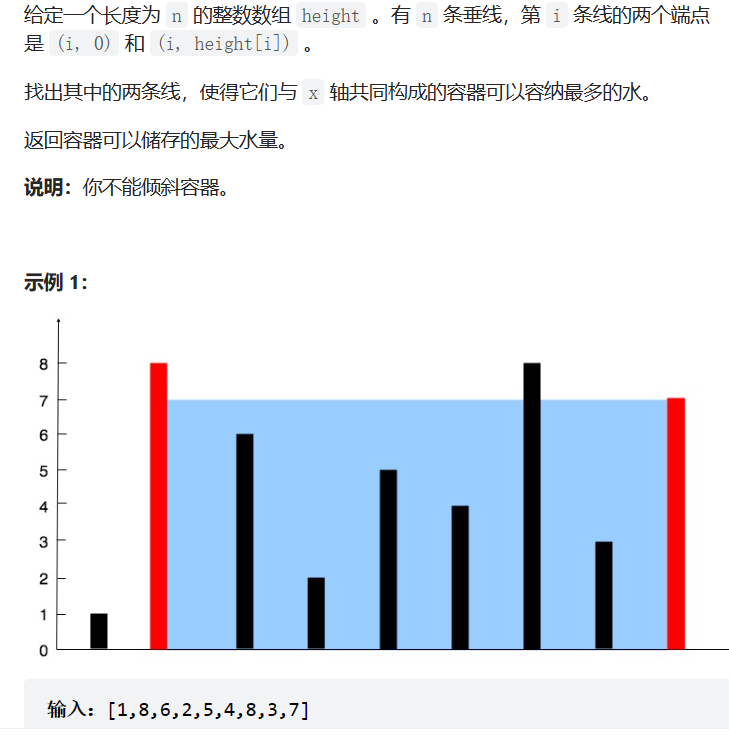
题目链接
int maxArea(vector<int>& height) {
int left=0,right=height.size()-1;
int max_area=min(height[0],height[right])*right;
while(left<right)
{
int area=(right-left)*min(height[left],height[right]);
max_area=max(max_area,area);
if(height[left]<height[right])
left++;
else right--;
//每次只移动一方因为一次只保证了一方的最大,那就移动小的那一边,去找更大的,并且每次移动一步也不会出现,越界问题,不需要在内层在去进行判断
}
return max_area;
}
我的想法:(这是有问题的)
left=0 , right=n-1
从做左开始,肯定要找一个高于left的,右边也一样
left–还是小于最早的left
right也是
那就继续二者都向前,直到有某一个大于
int maxArea(vector<int>& height) {
int left=0,right=height.size()-1;
int max_area=min(height[0],height[right])*right;
while(left<right)
{
int i=left;
while(i<right&&height[left]>=height[i])
{
i++;
}
left=i;
max_area=max(max_area,min(height[left],height[right])*(right-left));
int j=right;
while(j>left&&height[right]>=height[j])
j--;
right=j;
max_area=max(max_area,min(height[left],height[right])*(right-left));
}
return max_area;
}