【刷题之路Ⅱ】LeetCode 475. 供暖器
- 一、题目描述
- 二、解题
- 1、方法1——排序后二分法
- 1.1、思路分析
- 1.2、代码实现
- 2、方法2——排序后双指针
- 2.1、思路分析
- 2.2、代码实现
一、题目描述
原题连接: 475. 供暖器
题目描述:
冬季已经来临。 你的任务是设计一个有固定加热半径的供暖器向所有房屋供暖。
在加热器的加热半径范围内的每个房屋都可以获得供暖。
现在,给出位于一条水平线上的房屋 houses 和供暖器 heaters 的位置,请你找出并返回可以覆盖所有房屋的最小加热半径。
说明:所有供暖器都遵循你的半径标准,加热的半径也一样。
示例 1:
输入: houses = [1,2,3], heaters = [2]
输出: 1
解释: 仅在位置2上有一个供暖器。如果我们将加热半径设为1,那么所有房屋就都能得到供暖。
示例 2:
输入: houses = [1,2,3,4], heaters = [1,4]
输出: 1
解释: 在位置1, 4上有两个供暖器。我们需要将加热半径设为1,这样所有房屋就都能得到供暖。
示例 3:
输入: houses = [1,5], heaters = [2]
输出: 3
提示:
1 <= houses.length, heaters.length <= 3 * 104
1 <= houses[i], heaters[i] <= 109
二、解题
1、方法1——排序后二分法
1.1、思路分析
可能有的朋友在看完题目之后还搞不清楚题目要描述的场景,那我这里就先化身“灵魂画手”给大家画出场景图来:

如上图,题目中描述的场景大致如上图所示,假设地平线就是一根数轴,那么在这些数轴的坐标上分布着一些房子和供暖器,这些房子可能包围着一些供暖器,也有可能同一个坐标上同时有房子和供暖器,而这些供暖器也有可能不在房子的范围内。
我们要做的就是要找到一个最小的半径,以使得所有的供暖器在同时工作并且供暖半径相同的情况下能够供暖到所有的房子。
其实还有一点需要注意的是,如果一个坐标上同时存在房子和供暖器,那么久这个坐标上而言,这个供暖器的供暖半径为0就能够供暖到这个房子。
那我们应该怎样解决这个问题呢?
其实我们可以现针对每一个房子,找到离它最近的一个供暖器,那么这个供暖器能供暖到它的最小供暖半径就是他们的距离之差:
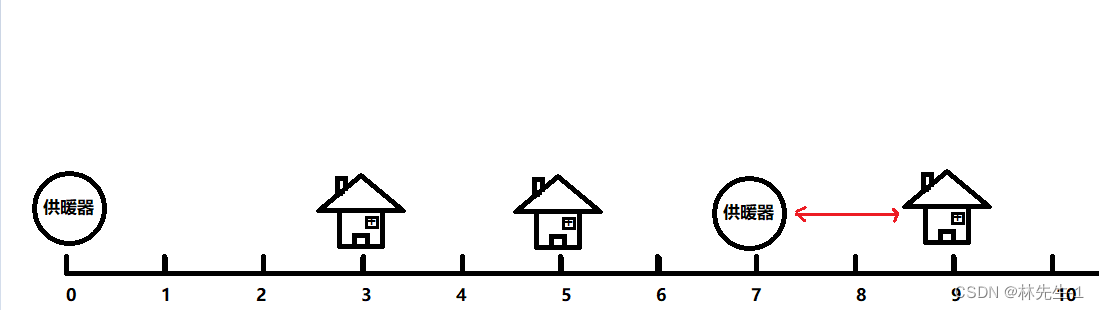
然后我们再求出每个房子到离它最近的供暖器的距离的最大值,这个最大值就是我们所要求的对于所有房子的最小供暖半径。
有些朋友可能会觉得有点儿绕啊,这一会儿最小值一会儿最大值的,这感觉怎么有点儿像我们在高中时候学的数学中的求函数的极值问题呢?
不过这个并没有函数极值那么绕人啦,其实就是需要满足所有房子都能被供暖到,所以我们才需要求最大值。
而在实际的操作中,为了找到距离某个房子的距离最小的供暖器,我们其实要找到两个供暖器,即左右两端最接近这个房子的供暖器,然后求出这两个距离的最小值即可:
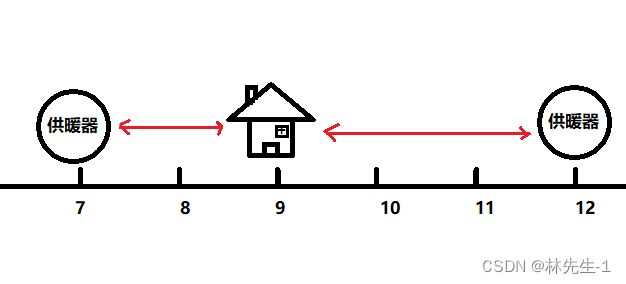
而如果对于某个房子的左端或右端没有供暖器的情况,很简单,我们就把这一段的距离设置长无穷大即可。
为了能更好的找到距离某个房子最近的供暖器,我们可以先将heaters数组进行排序,然后使用二分法找边界的方法找到第一个位置大于当前房子的位置的供暖器即可。
假设,heaters[j]为第一个位置大于houses[i],的供暖器,那么heaters[j]就是右端最接近houses[i]的供暖器,而heaters[j - 1]即是左端最接近houses[i]的供暖器。
1.2、代码实现
有了以上思路,那我们写起代码来也就水到渠成了:
int max(int x, int y) {
return x > y ? x : y;
}
int min(int x, int y) {
return x < y ? x : y;
}
int cmp_int(const void *p1, const void *p2) {
return *((int*)p1) - *((int*)p2);
}
// 二分法找边界法
int binarySearch(int *nums, int left, int right, int target) {
int numsSize = right + 1;
int mid = 0;
while (left < right) {
if (nums[left] > target) {
return left;
}
mid = left + (right - left) / 2;
if (nums[mid] <= target) {
left = mid + 1;
} else {
right = mid;
}
}
return nums[left] > target ? left : numsSize; // 如果没有找到,就返回数组的长度,表示找不到
}
int findRadius(int* houses, int housesSize, int* heaters, int heatersSize) {
// 先将数组heaters进行排序
qsort(heaters, heatersSize, sizeof(int), cmp_int);
int i = 0;
int minR = 0;
for (i = 0; i < housesSize; i++) {
int rightHeaterIndex = binarySearch(heaters, 0, heatersSize - 1,houses[i]);
int leftHeaterIndex = rightHeaterIndex - 1;
int leftDistance = leftHeaterIndex < 0 ? INT_MAX : houses[i] - heaters[leftHeaterIndex];
int rightDistance = rightHeaterIndex >= heatersSize ? INT_MAX : heaters[rightHeaterIndex] - houses[i];
int curR = min(leftDistance, rightDistance);
minR = max(curR, minR);
}
return minR;
}
时间复杂度:O((n+m)logn),其中m是数组houses的长度,n是数组heaters的长度,对数组heaters排序的复杂度为O(nlogn)。而对于houses中的每个元素,我们都得使用二分法在heaters数组中查找,复杂度为O(mlogn)。故合并的复杂度为O((n+m)logn)。
空间复杂度:O(logn),n为数组heaters的长度,空间复杂度主要取决于排序所需要的空间。
2、方法2——排序后双指针
2.1、思路分析
通过方法1的解法我们应该能够得到启发,其实对于每个房子我们只需要找到距离它最近的房子即可。
那么我们是否能再次优化以下呢?
当然是可以的,其实我们完全可以利用上一个房子查找的结构来辅助查找到下一个房子的离它最近的供暖器,例如:

如上图所示,离坐标为3的房子最近的是坐标为0的供暖器,那么对于下一个坐标为5的房子,离它最近的房子就只有可能是坐标为0的供暖器或者在坐标为0的供暖器右端的供暖器,这里很明显就是在在右端的坐标为7的供暖器。
所以这就很好地利用了上一个坐标为3的房子的查找结果了。
沿着这个思路,我们也能找到距离下标为5和9的房子最近的供暖器是同一个:

而这个操作正好可以使用双指针来完成,如下图:
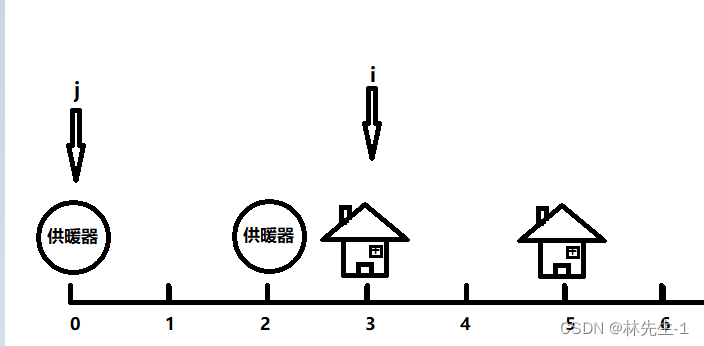
我们使用两个指针j和i分别来遍历供暖器和房子,当j的下一个供暖器距离i的距离更近的时候,就让j往前走,直到走到j的下一个供暖器距离i更远:
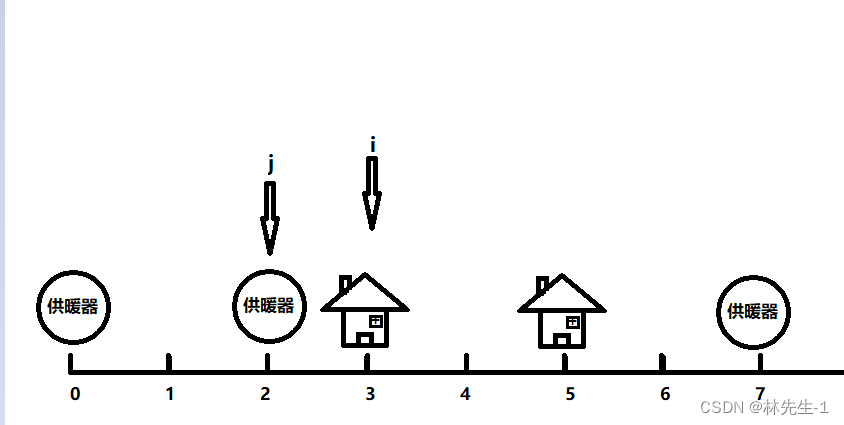
然后我们就记录这个距离,这就是距离i最近的供暖器的距离。
然后我们就让i完后走,查找下一个房子的。
2.2、代码实现
有了以上思路,那我们写起代码来也就水到渠成了:
int max(int x, int y) {
return x > y ? x : y;
}
int min(int x, int y) {
return x < y ? x : y;
}
int cmp_int(const void *p1, const void *p2) {
return *((int*)p1) - *((int*)p2);
}
int findRadius(int* houses, int housesSize, int* heaters, int heatersSize) {
// 先将两个数组进行排序
qsort(heaters, heatersSize, sizeof(int), cmp_int);
qsort(houses, housesSize, sizeof(int), cmp_int);
int minR = 0;
int curR = 0;
int i = 0;
int j = 0;
for (i = 0, j = 0; i < housesSize; i++) {
curR = abs(houses[i] - heaters[j]);
while (j < heatersSize - 1 && abs(houses[i] - heaters[j + 1]) <= abs(houses[i] - heaters[j])) {
j++;
curR = min(curR, abs(houses[i] - heaters[j]));
}
minR = max(curR, minR);
}
return minR;
}
时间复杂度:O(nlogn + mlogm),n和m分别是数组heaters和数组houses的长度。
空间复杂度:(logn + logm),空间复杂度主要取决于排序所需要的口空间。