（一）递归实现：

完整代码： 

#include<stdio.h>
#include<stdlib.h>
#include<iostream>
using namespace std;

#define MaxSize 100
typedef int ElemType;
typedef struct BiNode {
	ElemType data;
	BiNode* lchild;
	BiNode* rchild;

}BiNode, * BiTree;

//构建二叉树
BiNode* Create(BiNode* bt) {
	static int i = 0;
	char ch;
	//string str = "AB#D##C##";
	//string str = "124##56##7##3##";
	//string str = "ABD#G##E##CF###";
	string str = "ABD#GH##I##E##CF###";
	ch = str[i++];
	if (ch == '#')bt = NULL;//建立一棵空树 
	else {
		bt = (BiTree)malloc(sizeof(BiNode)); bt->data = ch;//生成一个结点，数据域为ch
		bt->lchild = Create(bt->lchild);//递归建立左子树
		bt->rchild = Create(bt->rchild);//递归建立右子树
	}
	return bt;
}

typedef struct {
	ElemType data[MaxSize];//存放栈中元素
	int top;//栈顶指针
}SqStack;

//（1）初始化
void InitStack(SqStack& S) {
	S.top = -1;//初始化栈顶指针
}
//（2）判栈空
bool IsEmpty(SqStack& S) {
	if (S.top == -1) {//栈空
		return true;
	}
	else {//不空
		return false;
	}
}
//（3）进栈
bool Push(SqStack& S, ElemType data) {
	if (S.top == MaxSize - 1) {//栈满，报错
		return false;
	}
	S.data[++S.top] = data;//指针先加1，再加入栈
	return true;
}
//（4）出栈
bool Pop(SqStack& S, ElemType &data) {
	if (S.top == -1) {//栈空，报错
		return false;
	}
	data = S.data[S.top--];//先出栈，指针再减1
	return true;
}
//（5）读栈顶元素
bool GetTop(SqStack& S, ElemType data) {
	if (S.top == -1) {//栈空，报错
		return false;
	}
	data = S.data[S.top];//先出栈，指针再减1
	return true;
}

bool Ancestors(BiNode* root,ElemType x, SqStack &S) {
	if (!root) return false;
	if (root->data == x) return true;
	if (Ancestors(root->lchild, x,S) || Ancestors(root->rchild, x, S)) {
		//printf("%c ", root->data);//G D B A
		Push(S, root->data);
		return true;
	}
	return false;
}

int main() {
	//创建一棵二叉树
	BiTree T = (BiTree)malloc(sizeof(BiNode));//创建一颗二叉树
	T = Create(T);
	SqStack S;
	InitStack(S);
	Ancestors(T, 'I',S);
	ElemType ch;
	while (!IsEmpty(S)) {
		Pop(S, ch);
		printf("%c ", ch); // A B D G
	}
}

 

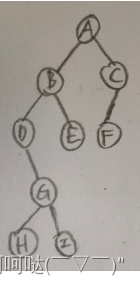
 （二）非递归实现：

因为查找的过程就是后序遍历的过程，因此使用的栈的深度不超过树的深度

完整的代码：

#include<stdio.h>
#include<stdlib.h>
#include<iostream>
using namespace std;

#define MaxSize 100
typedef char ElemType;
typedef struct BiNode {
	ElemType data;
	BiNode* lchild;
	BiNode* rchild;

}BiNode, * BiTree;

//构建二叉树
BiNode* Create(BiNode* bt) {
	static int i = 0;
	char ch;
	//string str = "AB#D##C##";
	//string str = "124##56##7##3##";
	//string str = "ABD#G##E##CF###";
	string str = "ABD#GH##I##E##CF###";
	ch = str[i++];
	if (ch == '#')bt = NULL;//建立一棵空树 
	else {
		bt = (BiTree)malloc(sizeof(BiNode)); bt->data = ch;//生成一个结点，数据域为ch
		bt->lchild = Create(bt->lchild);//递归建立左子树
		bt->rchild = Create(bt->rchild);//递归建立右子树
	}
	return bt;
}



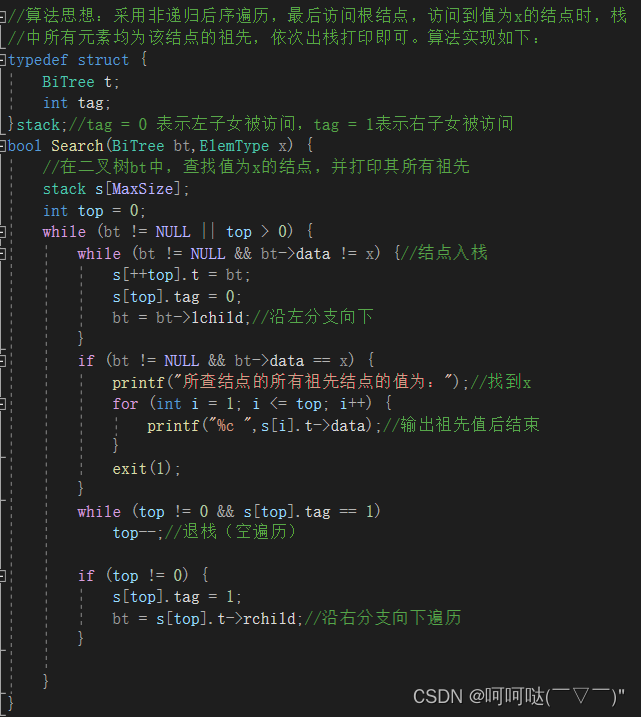
//算法思想：采用非递归后序遍历，最后访问根结点，访问到值为x的结点时，栈
//中所有元素均为该结点的祖先，依次出栈打印即可。算法实现如下：
typedef struct {
	BiTree t;
	int tag;
}stack;//tag = 0 表示左子女被访问，tag = 1表示右子女被访问
bool Search(BiTree bt,ElemType x) {
	//在二叉树bt中，查找值为x的结点，并打印其所有祖先
	stack s[MaxSize];
	int top = 0;
	while (bt != NULL || top > 0) {
		while (bt != NULL && bt->data != x) {//结点入栈
			s[++top].t = bt;
			s[top].tag = 0;
			bt = bt->lchild;//沿左分支向下
		}
		if (bt != NULL && bt->data == x) {
			printf("所查结点的所有祖先结点的值为：\n");//找到x
			for (int i = 1; i <= top; i++) {
				printf("%c ",s[i].t->data);//输出祖先值后结束
			}
			exit(1);
		}
		while (top != 0 && s[top].tag == 1)
			top--;//退栈（空遍历）

		if (top != 0) {
			s[top].tag = 1;
			bt = s[top].t->rchild;//沿右分支向下遍历
		}
		
	}
}

int main() {
	//创建一棵二叉树
	BiTree bt = (BiTree)malloc(sizeof(BiNode));//创建一颗二叉树
	bt = Create(bt);
	Search(bt, 'I');
}