---

title: 数据结构lab1-一元多项式的代数运算
date: 2023-05-16 11:42:26
tags: 数据结构与算法

---

git地址：https://github.com/944613709/HIT-Data-Structures-and-Algorithms

哈尔滨工业大学计算机科学与技术学院

实验报告

课程名称：数据结构与算法

课程类型：必修

实验项目：线性表的链式存储结构与应用

实验题目：一元多项式的代数运算

实验日期：2021.10.13

班级：2003001

学号：120L021011

姓名：石卓凡

一、实验目的

1． 掌握线性表顺序存储结构的特点及线性表在顺序存储结构中各种基本操作的实现。

2． 掌握线性表链式存储结构的特点及线性表在链式存储结构中各种基本操作的实现。

3．重点巩固和体会线性表在链式存储结构上的各种操作和应用。

二、实验要求及实验环境

实验要求：

设计线性表的（动态或静态）链式存储结构，并实现一元多项式的代数运算。

以链表存储一元多项式，在此基础上完成对多项式的代数操作。

1.能够输入多项式（可以按各项的任意输入顺序，建立按指数降幂排列的多项式）和输出多项式（按指数降幂排列）,以文件形式输入和输出，并显示。

2.能够计算多项式在某一点x=x0的值，其中x0是一个浮点型常量，返回结果为浮点数。

3.能够给出计算两个多项式加法、减法、乘法和除法运算的结果多项式，除法运算的结果包括商多项式和余数多项式。

4.要求尽量减少乘法和除法运算中间结果的空间占用和结点频繁的分配与回收操作。（提示：利用循环链表结构或可用空间表的思想，把循环链表表示的多项式返还给系统或可用空间表，从而解决上述问题）。

实验环境：

操作系统：Win7/Win10

集成开发环境：devcpp++

外部库：暂无

三、设计思想（本程序中的用到的所有数据类型的定义，主程序的流程图及各程序模块之间的调用关系）

1. 函数功能和外部接口设计

本系统总计设计了9个函数，每个函数的功能和接口设计如下表所示：

序号	函数名	函数功能	函数参数	函数返回值
1	Main	根据order执行各函数	无	无
2	ReadPoly	读入In1.txt或者In2.txt里的多项式，并以降幂顺序存储进链表	FILE *ff	Polynomial
3	Attach	将链表尾插一个新节点，赋值coef和expon	float c, int e, Polynomial* pRear	NULL
4	Add	加法，将结果存储至链表，返回表头	Polynomial P1, Polynomial P2	Polynomial
5	Sub	减法，将结果存储至链表，返回表头	Polynomial P1, Polynomial P2	Polynomial
6	Mult	乘法，将结果存储至链表，返回表头	Polynomial P1, Polynomial P2	Polynomial
7	Divide	除法，直接打印和输出结果	Polynomial P1, Polynomial P2	NULL
8	PrintPoly	根据链表表头将数据打印屏幕和输出到文件Out.txt	Polynomial P	NULL
9	Calulate	计算Xo的结果，直接打印和输出结果	Polynomial P,float x	NULL

2. 主程序的流程图及各程序模块之间的调用关系

*流程图及程序模块的调用关系*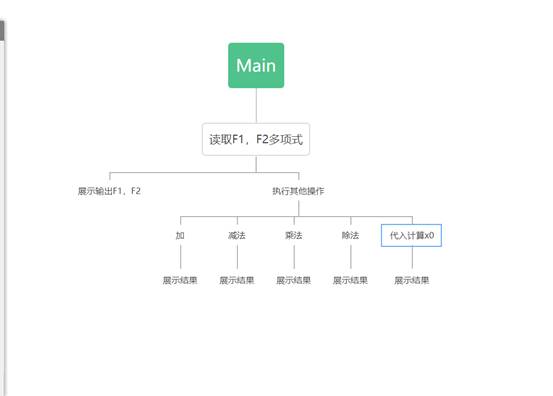

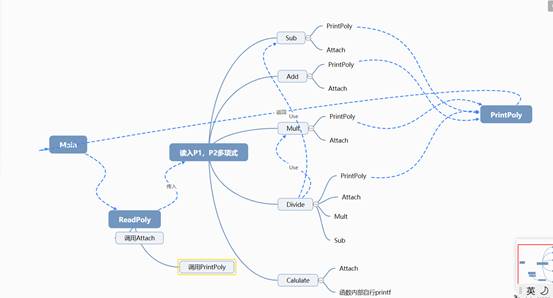
*各函数详细调用关系*

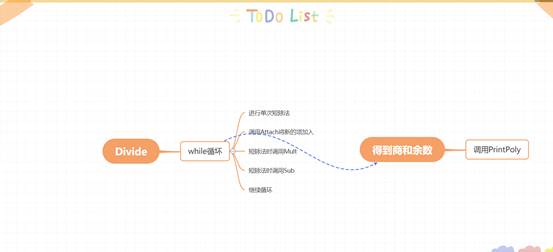
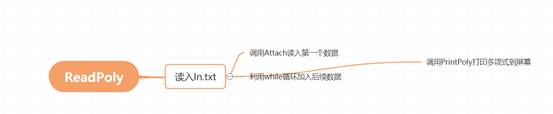
3. 数据类型的定义

typedef struct PolyNode *Polynomial;

struct PolyNode

{

**float coef; //**系数

**int expon; //**指数

Polynomial link;

}PolyNode;

**（一）**逻辑设计

(1) Attach插入项进入当前链表

\1. 新建结点t,将各个数值赋值

\2. 尾插法进入链表

(2) 从文件读入多项式

\1. 打开文件

\2. 创建链表的头结点

\3. 循环依次创建新节点，读入每一项的系数和指数，并且为尾插法Attach插入链表

\4. 删除空白头节点

（3) 加法

\1. 新建立链表头节点，和尾指针

\2. While循环，直到P1或者P2某个为空

2.1对于二者之间，拥有系数大的P，将P结点利用Attach(P1->coef,P1->expon,&Rear);插入链表

2.2对于二者之间，相同系数时候

2.2.1如果P1与P2当前系数和为0，则不用插入链表

2.2.2如果P1与P2当前系数和不为0，则插入链表Attach(P1->coef + P2->coef,P2->expon,&Rear);

3.while直到P1为空，不断Attach(P1->coef,P1->expon,&Rear);

4.While直到P2为空不断Attach(P2->coef,P2->expon,&Rear);

5.删除空白头节点

（4) 减法

\1. 新建链表头节点，和尾指针

\2. While循环直到P1或者P2某个为空

2.1对于二者之间，拥有系数大的P，将P结点利用Attach(P1->coef,P1->expon,&Rear);插入链表

2.2对于二者之间，相同系数时候

2.2.1如果P1与P2当前系数差为0，则不用插入链表

2.2.2如果P1与P2当前系数差不为0，则进行插入，Attach((P1->coef)-(P2->coef),P1->expon,&Rear);

\3. While直到P1为空Attach(P1->coef,P1->expon,&Rear)

\4. While直到P2为空Attach(-(P2->coef),P2->expon,&Rear);

\5. 删除空白头节点

（5) 乘法

\1. 如果P1或者P2为空则返回NULL，t1=P1，t2=P2

\2. 新建链表头节点=P

\3. While直到t1为空

(1) 赋值t2=P2,Rear=P

(2) While直到t2为空

① 计算当前t1和t2项乘法之后的系数和指数

② While循环去找到需要当前乘法结果需要插入的位置

③ 情况1在链表尾部插入，情况2在链表中间插入（Rear->link==NULL||Rear->link->expon < e）

④ 情况3（Rear->link->expon == e）当前可以进行合并

\1) 如果合并后是0则不需要插入，并且进行删除对应位置的节点

\2) 如果合并后不是0则进行插入

（6) 除法

a. 判断除数P2是否为0，如果是0则无法进行除法

b. 新建链表头节点，t1=P1,t2=P2

c. While一直循环

a) 计算当前商的项的指数newe和系数newc

b) 如果（P2->expon==0）当除数是常数（x是0次方）只需要出一次就能够得到，且余数多项式一定为0 。直接将Attach(newc,newe,&RearS);将商项插如商多项式。根据短除法，将Ptemp1 = Mult(RearS,P2)，Ptemp1 = Sub(t1,Ptemp1);t1=Ptemp1;并且结束循环break

c) 如果t1->expon < P2->expon已经达到了结束循环条件进行break

d) 否则，直接计算将Attach(newc,newe,&RearS);将商项插如商多项式。根据短除法，将Ptemp1 = Mult(RearS,P2)，Ptemp1 = Sub(t1,Ptemp1);t1=Ptemp1

（7) 计算x0

a. While循环

a) sum+=(P->coef)*pow(x,P->expon);

b) P=P->link;

**（二）**物理设计

表达式用链表存储，链表的结点就是表达式中的每一项用PolyNode表示，coef为系数，expon为指数，link指向下一项

struct PolyNode

{

float coef;

int expon;

Polynomial link;

}PolyNode;

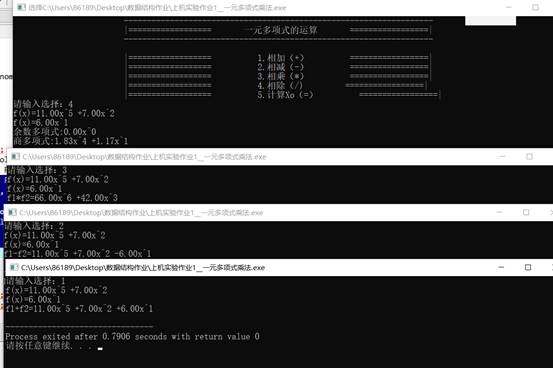
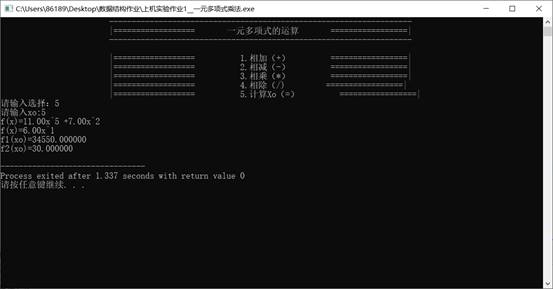
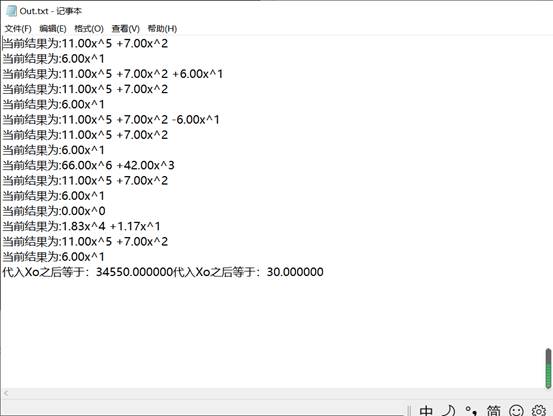
**四、**测试结果

测试用例1：

F1 = 1x^2-3x1+1x^0

F2 = 3x^3-5x1+6x^0

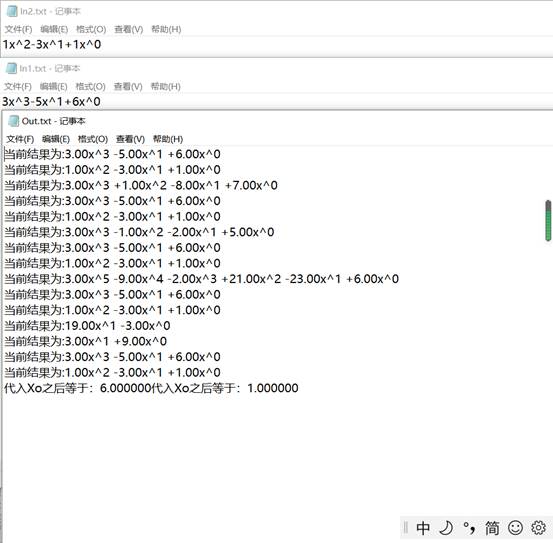
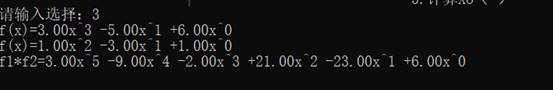
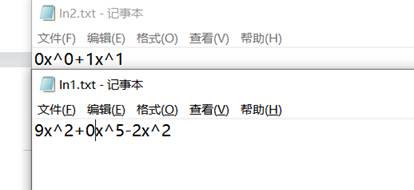
测试样例2

F1=9x^2+0x5-2x^2

F2=0x^0+1x1

**五、**经验体会与不足

不足：

1. 对于加减乘除后出现的系数为0的数据（比如0x^4)，前期没有考虑到究竟选择删除该节点还是保留，导致后期混乱没有统一

解决方法：统一为系数为0的数据删除节点，在ReadPoly中再进行补充条件防止输出为空

2. 对于最初尝试除法的函数时候，空间的占用和结点的删除过于频繁

解决方法：将原本定义了多个的Polynomial可以合并通用的都合并了，减少了相当一部分的多余使用

经验体会：

a. 对于一个程序需要多个测试样例来找出程序所存在的BUG和当前没有考虑到的情况，比如此程序中的极端情况，除数多项式为0时候不存在，比如最后输出0x^0时候的符号判定是个特殊情况

b. 链表中空间的占用和结点的释放需要多加注意，有很多重复使用的可以删掉，系数为0的也可以不用浪费结点

c. 对于尾插法和在中间插入一个节点，所使用到的代码都是通用的，可以将两块情况合并在一起。

六、附录：源代码（带注释）

\#include<stdio.h>

\#include<stdlib.h>

\#include<math.h>

typedef struct PolyNode *Polynomial;

struct PolyNode

{

  float coef;

  int expon;

  Polynomial link;

}PolyNode;

Polynomial ReadPoly(FILE *ff);

void Attach(float c, int e, Polynomial* pRear);

Polynomial Add(Polynomial P1, Polynomial P2);

Polynomial Sub(Polynomial P1, Polynomial P2);

Polynomial Mult(Polynomial P1, Polynomial P2);

void PrintPoly(Polynomial P);

void Calulate(Polynomial P,float x);

void Divide(Polynomial P1, Polynomial P2);

void Sort(Polynomial P);

int main()

{

​    Polynomial P1,P2,P;

​    FILE *fp1=NULL;

​    FILE *fp2=NULL;

​    fp1= fopen("In1.txt","r");

​    fp2= fopen("In2.txt","r");

​    printf("            -------------------------------------------------------------------\n");

  printf("            |==================    一元多项式的运算    =================|\n");

  printf("            -------------------------------------------------------------------\n\n");

  printf("            |==================     1.相加（+）     =================|\n");

  printf("            |==================     2.相减（-）     =================|\n");

  printf("            |==================     3.相乘（*）     =================|\n");

  printf("            |==================     4.相除（/)     =================|\n");

  printf("            |==================     5.计算Xo（=）     =================|\n");

  int n;

  printf("请输入选择：");

  scanf("%d",&n);

  switch (n)

  {

  case 3:

​          P1 = ReadPoly(fp1);

​            P2 = ReadPoly(fp2);

​            P=Mult(P1,P2);

​          printf("f1*f2="); 

​            PrintPoly(P);

​            break;

​    case 1:

​          P1 = ReadPoly(fp1);

​            P2 = ReadPoly(fp2);

​            P=Add(P1,P2);

​            printf("f1+f2="); 

​            PrintPoly(P);

​            break;

​    case 4:

​          P1 = ReadPoly(fp1);

​            P2 = ReadPoly(fp2);

​            Divide(P1,P2);//除法 

​            break;

​    case 2:

​          P1 = ReadPoly(fp1);

​            P2 = ReadPoly(fp2);

​            P=Sub(P1,P2);

​            printf("f1-f2="); 

​            PrintPoly(P);

​            break;

​    case 5:

​            float x;

​            printf("请输入xo:");

​            scanf("%f",&x);

​            P1 = ReadPoly(fp1);

​            P2 = ReadPoly(fp2);

​            printf("f1(xo)=");

​            Calulate(P1,x);

​            printf("f2(xo)=");

​            Calulate(P2,x);

​    }

​    fclose(fp1);

​    fclose(fp2);

}

void PrintPoly(Polynomial P)

{

​    FILE *p;

​    if((p=fopen("Out.txt","a"))==NULL)

​    {

​        printf("文件打开失败");

​        exit(0);

​    }

​    fprintf(p,"当前结果为:"); 

  int flag = 0;  // 判断是否是开头

  int Emptyflag = 1 ;//标记是否最终结果是否一个没输出，如果是1->Empty则输出0x^0 

  if (!P)

  {

​    printf("NULL");//当结果是NULL，P就是NULL,用以观测是否会出现P==NULL

​    fprintf(p,"NULL");

​    return;

  }

  while (P)

  {

​      if(P->coef==0) //对于0x^2直接跳过不输出 

​      {

​          P = P->link;

​          continue;

​        }

​        if(P->coef>0&&flag==1)//flag==1 不是开头则就要考虑+符号 

​            {

​            printf("+");

​            fprintf(p,"+"); 

​            }

​    printf("%.2fx^%d ", (P->coef), P->expon);

​    fprintf(p,"%.2fx^%d ", (P->coef), P->expon);

​    Emptyflag=0;//输出有非0数据

​    P = P->link;

​    if(flag==0)

​        flag=1;

  }

  if(Emptyflag==1)//如果P结果全是 0x^2+0x^1则只输出为0x^0 

  {

​      printf("0.00x^0");//结果为0总得输出一个

​    fprintf(p,"0.00x^0");

​    }

  printf("\n");

  fprintf(p,"\n");

  fclose(p);

}

Polynomial Mult(Polynomial P1, Polynomial P2)

{

​    Polynomial P,t1,t2,t,Rear;

​    if(!P1||!P2)

​        return NULL;//防止P1或P2万一为NULL，报错提示 

​    t1=P1;

​    t2=P2;

​    float c;

​    int e;

​    P=(Polynomial)malloc(sizeof(PolyNode));

​    P->link=NULL;

​    while(t1)//固定P1中的某个，依次遍历P2每一个 

​    {

​        t2=P2;

​        Rear=P;

​        while(t2)//t2==NULL 停下 

​        {

​            c=t1->coef * t2->coef;

​            e=t1->expon + t2->expon;

​            while(Rear->link!=NULL&&Rear->link->expon > e)//利用降幂顺序 来while循环找到插入的对应位置 

​                Rear=Rear->link;

​            if(Rear->link==NULL||Rear->link->expon < e)//在结尾插入（Rear->link==NULL） 和 在中间插入，都可以归为插入 

​            {                      //(Rear->link->expon)在中间插入

​                t=(Polynomial)malloc(sizeof(PolyNode));

​                t->coef=c;

​                t->expon=e;

​                t->link=Rear->link;

​                Rear->link=t;

​            }

​            else if(Rear->link->expon == e)//发现插入的可以合并同类项 

​            {

​                if(c + Rear->link->coef !=0)//合并之后不是0 

​                {

​                    Rear->link->coef += c;

​                }

​                else if (c + Rear->link->coef ==0)//合并之后为0直接删除结点 

​                {

​                    Polynomial temp;

​                    temp=Rear->link;

​                    Rear->link=Rear->link->link;

​                    free(temp);

​                }

​            }

​            t2=t2->link;

​        }

​        t1=t1->link;

​    }

​    t=P;

​    P=P->link;

​    free(t);

​    return P;

}

Polynomial Add(Polynomial P1, Polynomial P2)

{

​    Polynomial P,Rear,t;

​    P=(Polynomial)malloc(sizeof(PolyNode));

​    P->link=NULL;

​    Rear=P;

​    

​    while(P1&&P2)//从两个多项式依照降幂顺序，找指数高的开始 

​    {

​        if((P1->expon) > (P2->expon) )

​        {

​            Attach(P1->coef,P1->expon,&Rear);

​            P1=P1->link;

​        }

​        else if ((P1->expon) < (P2->expon))

​        {

​            Attach(P2->coef,P2->expon,&Rear);

​            P2=P2->link;

​        }

​        else

​        {   

​            if(P1->coef + P2->coef!=0)

​            {

​            Attach(P1->coef + P2->coef,P2->expon,&Rear);

​            P1=P1->link;

​            P2=P2->link;

​            }

​            else//coef = = 0

​            {

​            P1=P1->link;

​            P2=P2->link;

​            }//一旦系数为0都不存入结点 

​        }

​    }

​    while(P1)

​        {Attach(P1->coef,P1->expon,&Rear);

​            P1=P1->link;

​        }

​    while(P2)

​        {Attach(P2->coef,P2->expon,&Rear);

​            P2=P2->link;

​        }

​    t=P;

​    P=P->link;

​    free(t);

​    if(!P)

​    {

​        P=(Polynomial)malloc(sizeof(PolyNode));

​        P->link=NULL;

​        P->coef =0;

​        P->expon =0;

​    }//当结果为0时候防止P==NULL,不妨将新建结点，数据为0x^0

​    return P;

}

Polynomial Sub(Polynomial P1, Polynomial P2) //P1-P2  

{

​    Polynomial P,Rear,t;

​    P=(Polynomial)malloc(sizeof(PolyNode));

​    P->link=NULL;

​    Rear=P;

​    while(P1&&P2)

​    {

​        if((P1->expon) > (P2->expon) )//按照降幂这么放入P 

​        {

​            Attach(P1->coef,P1->expon,&Rear);

​            P1=P1->link;

​        }

​        else if ((P1->expon) < (P2->expon))

​        {

​            Attach(-(P2->coef),P2->expon,&Rear);

​            P2=P2->link;

​        }

​        else if ((P1->expon) == (P2->expon))

​        {   

​            if((P1->coef) -(P2->coef) == 0)

​            {

​                P1=P1->link;

​                P2=P2->link;

​            }

​            else

​            {

​                Attach((P1->coef)-(P2->coef),P1->expon,&Rear);

​                P1=P1->link;

​                P2=P2->link;

​            }

​        }

​    }

​    while(P1)

​        {Attach(P1->coef,P1->expon,&Rear);

​            P1=P1->link;

​        }

​    while(P2)

​        {Attach(-(P2->coef),P2->expon,&Rear);

​            P2=P2->link;

​        }

​    t=P;

​    P=P->link;

​    free(t);

​    if(!P)

​    {

​        P=(Polynomial)malloc(sizeof(PolyNode));

​        P->link=NULL;

​        P->coef =0;

​        P->expon =0;

​    }//当结果为0时候防止P==NULL,不妨将新建结点，数据为0

​    return P;

}

 

void Attach(float c, int e, Polynomial* pRear)

{

​    Polynomial t;

​    t=(Polynomial)malloc(sizeof(PolyNode));

​    t->coef=c;

​    t->expon=e;

​    t->link=NULL;

​    (*pRear)->link=t;//利用尾插法，当然要将尾结点指向更新，*pRear才能修改尾结点自己地址 

​    *pRear=t;

}

Polynomial ReadPoly(FILE *ff)

{

​    int exp;

​    float coe;

​    char ch;

​    Polynomial P,Rear,t,Head;

​    P=(Polynomial)malloc(sizeof(PolyNode));

​    P->link=NULL;

​    Rear=P;

  ch = fgetc(ff);

  if(ch==EOF)//看txt文本是否为空 

  {

​      printf("ERROR: In.txt输入为空");

​        exit(0);

​    }

  if(ch!='-')//3x^2+3x^1这种首项第一个不会带有+，特殊情况 

  {

​      rewind(ff);

​      fscanf(ff,"%fx^%d",&coe,&exp);

​      Attach(coe,exp,&Rear);

​    }

​    else//ch='-'

​    {

​        fscanf(ff,"%fx^%d",&coe,&exp);

​        Attach((-coe),exp,&Rear);

​    }

​    while(fscanf(ff,"%c%fx^%d",&ch,&coe,&exp)!=EOF)//开始按照降幂插入 

​    {

​        if(ch=='-')//如果是符号要调整coe 

​            coe=-coe;

​            

​        Head=P;

​        while(Head->link!=NULL&&Head->link->expon > exp ) //

​            Head=Head->link;

​        if(Head->link==NULL||Head->link->expon < exp)

​            {

​                t=(Polynomial)malloc(sizeof(PolyNode));

​                t->coef=coe;

​                t->expon=exp;

​                t->link=Head->link;

​                Head->link=t;

​            }

​        else if(Head->link->expon == exp)

​            {

​                if(coe + Head->link->coef !=0)

​                {

​                    Head->link->coef += coe;

​                }

​                else if (coe + Head->link->coef ==0)

​                {

​                    t=Head->link;

​                    Head->link=Head->link->link;

​                    free(t);

​                }//对于0x^2这种数据直接删掉结点 

​            }

​    }

​    t=P;

​    P=P->link;

​    free(t);

​    printf("f(x)=");

​    PrintPoly(P);

​    return P;//若In.txt为空则输出0x^0 

}

void Calulate(Polynomial P,float x)

{

​    FILE *p;

​    if((p=fopen("Out.txt","a"))==NULL)

​    {

​        printf("文件打开失败");

​        exit(0);

​    }

​    float sum;

​    sum=0;

​    while(P)

​    {

​        sum+=(P->coef)*pow(x,P->expon);

​        P=P->link;

​    }

​    printf("%f",sum);

​    fprintf(p,"代入Xo之后等于：%f",sum);

​    fclose(p);

​    printf("\n");

}

void Divide(Polynomial P1, Polynomial P2)//p1 / p2 

{

​    Polynomial PS,t1,t2,RearS,Ptemp1,t;

​    PS=(Polynomial)malloc(sizeof(PolyNode));//商多项式 

​    PS->link=NULL;

​    RearS=PS;//用来存储

​    t1=P1;

​    t2=P2;

​    if(P2->coef==0&&P2->expon==0)//当除数时0，数学公式不成立

​        {

​            printf("ERROR：P2不能为0");

​            exit(0);

​        }

​    float newc; 

​    int newe;

​    while(1)//进入循环

​    {

​        if(P2->expon==0)//特殊情况，当除数是常数（x是0次方）只需要出一次就能够得到，且余数多项式一定为0 

​            {

​            newe=t1->expon - P2->expon;//本次依次得到的商的一个项的指数 

​            newc=t1->coef / P2->coef;//本次依次得到的商的一个项的系数

​            Attach(newc, newe, &RearS);//将当前项，加入到商多项式

​            Ptemp1 = Mult(RearS,P2);//PP1*P2 = Ptemp，除法公式用到的 

​        Ptemp1 = Sub(t1,Ptemp1);//除法公式用到的 

​        t1=Ptemp1;//再次进行，当前短除法之后得到的余数多项式（不一定是最终的余数），成为新的t1，继续试探 

​        break;

​            }

​      if(t1->expon < P2->expon)

​        {

​            //已经完成商多项式 余数多项式

​            //t1就是最终余数多项式

​            break;//终止循环唯一条件

​        }

​        else//需要继续除 

​        {

​            newe=t1->expon - P2->expon;//本次依次得到的商的一个项的指数 

​            newc=t1->coef / P2->coef;//本次依次得到的商的一个项的系数

​            Attach(newc, newe, &RearS);//将当前项，加入到商多项式

​            Ptemp1 = Mult(RearS,P2);//PP1*P2 = Ptemp

​        Ptemp1 = Sub(t1,Ptemp1);

​        t1=Ptemp1;//再次进行，当前短除法之后得到的余数多项式（不一定是最终的余数），成为新的t1，继续试探 

​        }

​    }

​    t=PS;

​    PS=PS->link;

​    free(t);//删掉PS空白头结点 

​    if(!PS)//对于0/9x = 0 ..9x  此时防止商为空 

​    {

​    PS=(Polynomial)malloc(sizeof(PolyNode));//商多项式 

​    PS->link=NULL;

​    PS->coef = 0;

​    PS->expon = 0;

​    }

​    printf("余数多项式:");

​    PrintPoly(t1);//开始输出余数多项式 

​    printf("商多项式:");

​    PrintPoly(PS);//已经完成输出商多项式 

}