LC-1335. 工作计划的最低难度（区间DP、记忆化搜索==＞动态规划）

news2024/11/23 3:09:02

1335. 工作计划的最低难度

难度困难97

你需要制定一份 d 天的工作计划表。工作之间存在依赖，要想执行第 i 项工作，你必须完成全部 j 项工作（ 0 <= j < i）。

你每天至少需要完成一项任务。工作计划的总难度是这 d 天每一天的难度之和，而一天的工作难度是当天应该完成工作的最大难度。

给你一个整数数组 jobDifficulty 和一个整数 d，分别代表工作难度和需要计划的天数。第 i 项工作的难度是 jobDifficulty[i]。

返回整个工作计划的 最小难度 。如果无法制定工作计划，则返回 -1 。

示例 1：

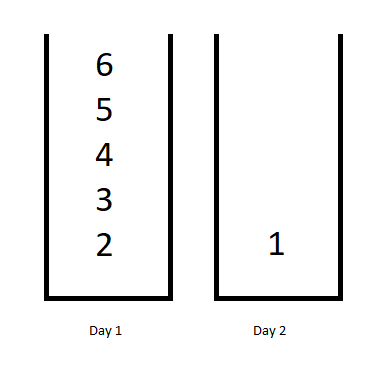
输入：jobDifficulty = [6,5,4,3,2,1], d = 2
输出：7
解释：第一天，您可以完成前 5 项工作，总难度 = 6.
第二天，您可以完成最后一项工作，总难度 = 1.
计划表的难度 = 6 + 1 = 7

示例 2：

输入：jobDifficulty = [9,9,9], d = 4
输出：-1
解释：就算你每天完成一项工作，仍然有一天是空闲的，你无法制定一份能够满足既定工作时间的计划表。

示例 3：

输入：jobDifficulty = [1,1,1], d = 3
输出：3
解释：工作计划为每天一项工作，总难度为 3 。

示例 4：

输入：jobDifficulty = [7,1,7,1,7,1], d = 3
输出：15

示例 5：

输入：jobDifficulty = [11,111,22,222,33,333,44,444], d = 6
输出：843

提示：

1 <= jobDifficulty.length <= 300
0 <= jobDifficulty[i] <= 1000
1 <= d <= 10

（区间DP）记忆化搜索 ==> 动态规划

题解：https://leetcode.cn/problems/minimum-difficulty-of-a-job-schedule/solution/by-zhou-pen-cheng-ab2b/

题意：

给定d天，每天都要完成至少一份工作，且按照数组的顺序。

如果工作数少于天数，那么最后一定有未安排工作的日子
如果工作数等于天数，那么每天只能依次安排一个工作
更一般的情况，可用动态规划来求解

状态定义：

f[i][j]表示考虑前i个工作，即job[0,...,i-1]，时间为j天的答案。

最后返回的答案应该是f[n][d]，其中n = len(job)

状态转移

f[i][j]可以将job[i-1]单独安排在第j天做，将前i-1个工作，安排在前j-1天

更一般的可以将job[i-k,...,i-1]安排在第j天做，将前i-k个工作，安排在前j-1天

f[i][j]=f[i−k][j−1]+max(job[i−1,...,i-k])

我们可以遍历所有合法的k值，取这些方案答案的最小值。

因为第j天必须要安排一份工作，所以最少也得安排job[i-1]，即 k >= 1
因为工作数不能少于工作天数，所以要求i - k >= j - 1 即 k <= i - j + 1

所以状态转移方程为：

在这里插入图片描述

在进行状态转移时，j <= i 才能保证至少每天都有一份工作，当然j还不能超过题目设定的天数d

细节：

注意到状态转移方程中，有一项求最大值的操作，为了优化时间复杂度，可以将job区间最大值预先处理出来，如何求区间最大值就很简单了。g[i][j]表示job[i,...,j]的最大值。

class Solution:
    def minDifficulty(self, jobDifficulty: List[int], d: int) -> int:
        n = len(jobDifficulty)
        if d > n:
            return -1 # 就算你每天完成一项工作，仍然有一天是空闲的
        # 预处理出区间的最大值
        dp = [[0 for _ in range(n)] for _ in range(n)]
        for i in range(n):
            dp[i][i] = jobDifficulty[i]
            for j in range(i, n):
                if j == 0: continue
                dp[i][j] = max(dp[i][j-1], jobDifficulty[j])
        
        # f[i][j]可以将job[i-1]单独安排在第j天做，将前i-1个工作，安排在前j-1天
        # 更一般的可以将job[i-k,...,i-1]安排在第j天做，将前i-k个工作，安排在前j-1天
        @cache
        def dfs(i: int, j: int) -> int:
            if j == 1:
                return dp[0][i-1]
            ans = float('inf')
            for k in range(1, i-j+2):
                ans = min(ans, dfs(i-k, j-1) + dp[i-k][i-1])
            return ans
        return dfs(n, d)

记忆化搜索转递推

class Solution:
    def minDifficulty(self, jobDifficulty: List[int], d: int) -> int:
        n = len(jobDifficulty)
        if d > n:
            return -1 # 就算你每天完成一项工作，仍然有一天是空闲的
        # 预处理出区间的最大值
        dp = [[0 for _ in range(n)] for _ in range(n)]
        for i in range(n):
            dp[i][i] = jobDifficulty[i]
            for j in range(i, n):
                if j == 0: continue
                dp[i][j] = max(dp[i][j-1], jobDifficulty[j])
        
        # f[i][j]表示考虑前i个工作，即job[0,...,i-1]，时间为j天的答案。
        f = [[float('inf') for _ in range(d+1)] for _ in range(n+1)]
        f[0][0] = 0
        for i in range(1, n+1):
            for j in range(1, min(i+1, d+1)):
                for k in range(1, i-j+2):
                    f[i][j] = min(f[i][j], f[i-k][j-1] + dp[i-k][i-1])
        return f[n][d]