A-0-1翻转_第二十届宁波大学程序设计竞赛(同步赛) (nowcoder.com)
思路:
- 我们观察发现,奇数位与偶数位的1每次操作一定时同时增加或者减少的,我们无法做到同时删除奇数位的两个1.。不满足相等则情况无解
- 那么,我们考虑,删除 两个1需要的最小步骤:如11需要1步,1001需要3步,100001需要5步。
- 我们猜测需要的步数就是他们的距离差。
- 观察发现我们每2步操作,一定可以使一个1移动2位去靠近可以一起消去的1,而且操作结束后其他位置的数不变
- 如1001->1111->1100,我们花2步,使右边1靠近了左边1
- 如1011->1000->1110
- 所以,我们只需要贪心存入奇数位1与偶数位1的下标,每次取最小的两个下标的距离差即可
#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define endl "\n"
#define int long long
typedef pair<int, int> pii;
//---------------------------------------------------------------------------------------------------------------------//
//---------------------------------------------------------------------------------------------------------------------//
//double 型memset最大127,最小128
const int INF = 0x3f3f3f3f; //int型的INF
const ll llINF = 0x3f3f3f3f3f3f3f3f;//ll型的llINF
const int N = 3e5 + 10;
void mysolve()
{
vector<int>a,b;
int n;
string s;
cin>>n>>s;
for(int i=0; i<n; ++i)if(s[i]=='1')
{
if(i&1)a.push_back(i);
else b.push_back(i);
}
if(a.size()!=b.size())cout<<-1<<endl;
else
{
int ans=0;
for(int i=0; i<(int)a.size(); ++i)ans+=abs(a[i]-b[i]);
cout<<ans<<endl;
}
}
int32_t main()
{
std::ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
ll t=1;
cin >> t;
while (t--)
{
mysolve();
}
system("pause");
return 0;
}C-平泽唯删圆_第二十届宁波大学程序设计竞赛(同步赛) (nowcoder.com)
思路:
写在这里:求两圆相交的面积_WQhuanm的博客-CSDN博客
I-库洛牌小喵钓鱼
思路:
-
尝试推导概率dp的状态转移方程 。设dp[i]表示中间剩i张排可以到达的情况
-
发现重新组合的情况数就是排列(i+2)!,中间的数随机排列的情况是(i)!,外面两张王的情况是2。考虑两张王的放发,推导出
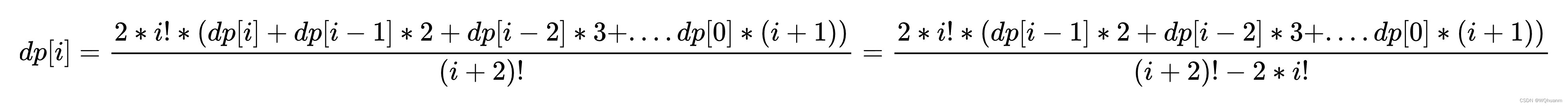
-
#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define endl "\n"
#define int long long
const int N = 3e5 + 10;
const ll mod=998244353;
int dp[N],pre[N],sum[N],lei[N];
ll fastmi(ll base,ll power)
{
ll ans=1;
while(power)
{
if(power&1)ans=ans*base%mod;
base=base*base%mod;
power>>=1;
}
return ans;
}
void mysolve()
{
int n;
cin>>n;
cout<<dp[n]<<endl;
}
int32_t main()
{
std::ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
ll t=1;
dp[0]=1,dp[1]=0;
pre[0]=1;
for(int i=1; i<=2e5+10; ++i)pre[i]=pre[i-1]*i%mod;//预处理排列数
sum[1]=1,lei[1]=3;
for(int i=2; i<=2e5; ++i)
{
dp[i]=2ll*pre[i]%mod*lei[i-1]%mod*fastmi((pre[i+2]-2ll*pre[i]%mod+mod)%mod,mod-2ll)%mod;
sum[i]=(sum[i-1]+dp[i])%mod;//记录每个dp的和
lei[i]=((lei[i-1]+sum[i])%mod+dp[i])%mod;//记录累积结果
}
cin >> t;
while (t--)
{
mysolve();
}
system("pause");
return 0;
}
J-双端队列_第二十届宁波大学程序设计竞赛(同步赛) (nowcoder.com)
思路:
- 先考虑暴力的做法(即不优化查询与删除操作):那我们只需要两个指针(l,r)分别表示队头与队尾,每次增加的时候移动指针,同时记录每个位置对应的数即可。
- 我们发现每次删除只与x有关,那能不能记录每次x出现对应的下标呢,删除的时候把这个位置去掉即可(不是真去掉,是标记这个位置为空)(map<int,vector<int>>可以).
- 这样成功优化删除,而你会发现,接下来查询的操作就是在(l~r)的区间内遍历到x个元素,如果遇到已经被标记为删除的,跳过不计。所以,我们就是每次查区间第x个元素。显然用线段树就可以区间查询目前有效的第x个位置。这样查询也成功优化。
#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define endl "\n"
#define int long long
typedef pair<int, int> pii;
//---------------------------------------------------------------------------------------------------------------------//
//---------------------------------------------------------------------------------------------------------------------//
//double 型memset最大127,最小128
const int INF = 0x3f3f3f3f; //int型的INF
const ll llINF = 0x3f3f3f3f3f3f3f3f;//ll型的llINF
const int N = 2e6 + 10;
#define mid (t[p].l+((t[p].r-t[p].l)>>1))
#define ls p<<1
#define rs p<<1|1
struct tree
{
int l,r;
int sum;
} t[N<<2];
int a[N];
void build(int l,int r,int p)
{
t[p].l=l,t[p].r=r,t[p].sum=0;
if(l==r)return;
build(l,mid,ls);
build(mid+1,r,rs);
}
void update(int x,int p,int val)
{
if(t[p].l==t[p].r&&t[p].l==x)
{
t[p].sum+=val;//维护当前区间存在几个实际存在未被删除的数
return;
}
if(mid>=x)update(x,ls,val);
else update(x,rs,val);
t[p].sum=t[ls].sum+t[rs].sum;
}
int ask(int x,int p,int sum)
{
if(t[p].l==t[p].r)return t[p].l;
if(sum+t[ls].sum>=x)return ask(x,ls,sum);
else return ask(x,rs,sum+t[ls].sum);
}
void mysolve()
{
int n,x;
map<int,vector<int>>mp;
cin>>n;
build(1,2*n,1);
int l=n,r=n+1;
char op;
while(n--)
{
cin>>op>>x;
if(op=='F')
{
update(l,1,1);
a[l]=x;
mp[x].push_back(l--);
}
else if(op=='B')
{
update(r,1,1);
a[r]=x;
mp[x].push_back(r++);
}
else if(op=='D')
{
if(mp.count(x)&&mp[x].size()>0)//每次访问x最后一次插入的位置
{
update(mp[x].back(),1,-1);
mp[x].pop_back();
}
}
else
{
if(t[1].sum>=x)cout<<a[ask(x,1,0)]<<endl;
else cout<<-1<<endl;
}
}
}
int32_t main()
{
std::ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
ll t=1;
cin >> t;
while (t--)
{
mysolve();
}
system("pause");
return 0;
}