31012 - 贴瓷砖

时间限制 : 1 秒

内存限制 : 32 MB

有一块大小是 2 * n 的墙面，现在需要用2种规格的瓷砖铺满，瓷砖规格分别是 2 * 1 和 2 * 2，请计算一共有多少种铺设的方法。

输入

输入的第一行包含一个正整数T（T<=20），表示一共有T组数据，接着是T行数据，每行包含一个正整数N（N<=30），表示墙面的大小是2行N列。

输出

输出一共有多少种铺设的方法，每组数据的输出占一行。

样例

输入

输出

3
171
2731

答案：

#include<iostream>
using namespace std;
int main() {
	int T = 0;
	cin >> T;
	int num = 0;
	while (T) {
		long long f1 = 1, f2 = 3,f3=0;
		cin >> num;
		if (num == 1) {
			f3 = f1;
		}
		else if (num == 2) {
			f3 = f2;
		}
		else {
			for (int i = 3; i <= num; i++) {
				f3 = 2*f1 + f2;
				f1 = f2;
				f2 = f3;
			}
		}
		cout << f3 << endl;
		T--;
	}
	return 0;
}

分析：如果你之前见到过这个题的话其实不难，但是如果第一次见，还是有点难度的。下面我们开始分析：

如果是2*1的瓷砖，很显然只有一种贴法，那就是用一块2*1的砖贴即可，记f1=1

如果是2*2，为什么有三种呢？一种就是直接用一块2*2的砖贴，第二种就是用两块2*1的砖横着贴，既然可以横着贴，那么就可以竖着贴，因此第三种就是用两块2*1竖着贴。共三种。记f2=3

如果是2*3，还要一个一个分析么？不用了，我们知道2*3，前面的2*2用一块2*2的瓷砖贴，剩下的用一块2*1的砖贴，因此贴法就是2*2的贴法种数，共3种，

如果前2*2用2*1的瓷砖来贴，那么显然就只能用2*1的砖横着贴或者竖着贴，因此有2*f1种，共f2+2*f1种，因此f3=f2+f1*2.这个递推式第一次推倒还是有点难度的，很多人不会想到那个瓷砖除了横着贴，还能竖着贴。这是本题的一个核心。

是否通过：

31013 - 统计方案

时间限制 : 1 秒

内存限制 : 32 MB

在一无限大的二维平面中，我们做如下假设：

1、每次只能移动一格；

2、不能向后走（假设你的目的地是“向上”，那么你可以向左走，可以向右走，也可以向上走，但是不可以向下走）；

3、走过的格子立即塌陷无法再走第二次。

求走n步不同的方案数（2种走法只要有一步不一样，即被认为是不同的方案）。

输入

首先给出一个正整数C，表示有C组测试数据。

接下来的C行，每行包含一个整数n（n<=20），表示要走n步。

输出

请编程输出走n步的不同方案总数；每组的输出占一行。

样例

输入

2
1
2

输出

3
7

答案：

#include<iostream>
using namespace std;
int main() {
	int N;
	cin >> N;
	int num;
	while (N) {
		cin >> num;
		long long f1 = 3, f2 = 7, f3 = 0;
		if (num == 1) {
			f3 = f1;
		}
		else if (num == 2) {
			f3 = f2;
		}
		else {
			for (int i = 3; i <= num; i++) {
				f3 = 2 * f2 + f1;
				f1 = f2;
				f2 = f3;
			}
		}
		cout << f3 << endl;
		N--;
	}
	return 0;
}

分析：本题的核心是推倒出那个递推关系，这个是不太容易直接看出来的，递推公式是

f(n)=2*f(n-1)+f(n-2)

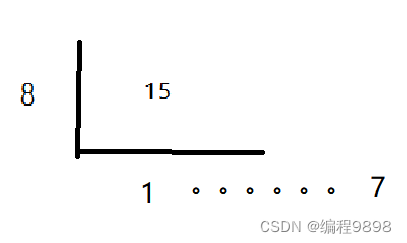
可以在图上画出来看看，我画一个f(3)的情况：

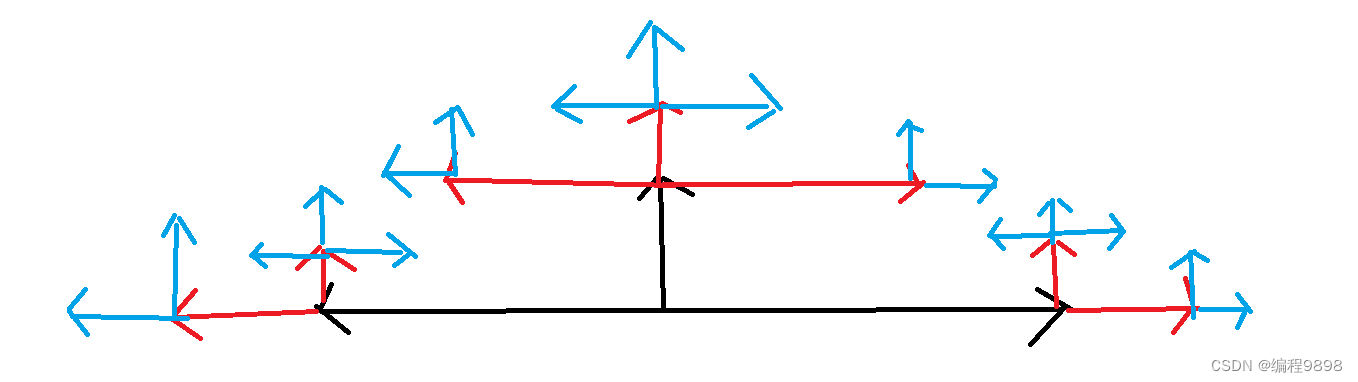
其中黑色为n==1时时的走法，有3种，

红色为n==2 时的走方法，有7种

蓝色为n==3时的走法，有17总，不难看出，17=3+2*7，那个就是顶端的3种走法，两边都是7，则2*7.因此可以类推:

f(n)=2*f(n-1)+f(n-2)

是否通过：

31014 - 小明的烦恼（推导难度大）

时间限制 : 1 秒

内存限制 : 32 MB

小明最近新买了一个房间，为了给它做装修，想要给它铺上地砖。然而现有的地砖只有两种规格分别为1米*1米、2米*2米，由于小明买的房间有点小，宽度只有3米，长度为N米。当然这样一个房间也足够他自己一个人住了。那么如果要给这个房间铺设地砖，且只用以上这两种规格的地砖，请问有几种铺设方案。

输入

输入的第一行是一个正整数C，表示有C组测试数据。接下来C行，每行输入一个正整数n（1<=n<=30），表示房间的长度。

输出

对于每组输入，请输出铺设地砖的方案数目。

样例

输入

2
2
3

输出

3
5

答案：

#include<iostream>
using namespace std;
int main() {
	int N;
	cin >> N;
	int ans = 0;
	while (N) {
		cin >> ans;
		long long  f1 = 1, f2 = 3, f3 = 0;
		if (ans == 1) {
			f3 = 1;
		}
		else if (ans == 2) {
			f3 = 3;
		}
		else {
			for (int i = 3; i <= ans; i++) {
				f3 = f2 + 2 * f1;
				f1 = f2; 
				f2 = f3;
			}
		}
		cout << f3 << endl;
		N--;
	}
	
	return 0;
}

分析：这个题和前面那个贴瓷砖是一个类型的题目，但是又有区别。开始分析：

当N=1时，很显然，这个时候只有一种方法。即只能用1*!的砖，即f1=1

当N=2时，全部用1*1，是一种，前面2*2的格子用2*2的砖贴，后面的用1*1的砖贴，或者后面2*2的格子用2*2的砖贴，共2种，一共3种，即f2=3,贴法如下：

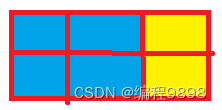
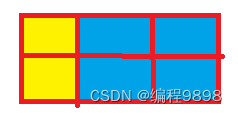
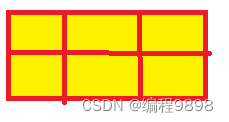
当N=3时，这个时候，就得靠推导了，看下图：

最后一行行贴1*1，那么剩下的就是3*2的贴法。因此有f2种。

最后两行有两种贴法，仔细观察你，是2*1种，因此共f3=f2+2*f1种，以此类推。。f(n)=f(n-1)+2*f(n-2)。

是否通过：

31015 - 十进制数转换成八进制（递归升级版）

时间限制 : 1 秒

内存限制 : 128 MB

用递归算法，把任一给定的十进制正整数转换成八进制数输出。

输入

一个正整数，表示需要转换的十进制数。

输出

一个正整数，表示转换之后的八进制数。

样例

输入

输出

答案：

#include<iostream>
using namespace std;

void f(int N) {
	if (N < 8) {
		cout << N;
	}
	else {
		f(N / 8);
		cout << N % 8;
	}
}
int main() {
	int N;
	cin >> N;
	f(N);
	return 0;
}

分析：要说实现十进制转八进制其实不难，但是要用递归实现就比较难了。在以前我们就知道通过短除法来求进制之间的转换。如下图，

当这个数小于8时，从该数开始，从下往上打印余数，就得了8进制数，其他进制数也是如此。

因此递归条件就是：

N<8时开始打印，

N>8时，除以8，然后打印它与8的余数。

这个递归看似简单，第一次还是很难写出来的，一定要掌握递归条件，才能写出来。

31016 - 小明养猪的故事（昆虫繁殖简化版）

时间限制 : 1 秒

内存限制 : 128 MB

话说现在猪肉价格这么贵，小明也开始了养猪生活。说来也奇怪，他养的猪一出生第二天开始就能每天中午生一只小猪，而且生下来的竟然都是母猪。
不过光生小猪也不行，小明采用了一个很奇特的办法来管理他的养猪场：
对于每头刚出生的小猪，在它生下第二头小猪后立马被杀掉，卖到超市里。
假设在创业的第一天，小明只买了一头刚出生的小猪，请问，在第N天晚上，小明的养猪场里还存有多少头猪？

输入

测试数据的第一行是一个正整数T，代表测试数据的个数。接下来有T组测试，每组测试数据占一行，分别是一个正整数N，代表小明创业的第N天。（0<N<20）

输出

对于每组数据，请在一行里输出第N天晚上养猪场里猪的数目。

样例

输入

2
2
3

输出

2
3

答案：

#include<iostream>
using namespace std;
int main() {
	int T;
	cin >> T;
	int a[20] = { 0,1,2,3 };//第i天晚上猪的总数
	int b[20] = { 0,0,1,2 };//第i天新出生猪的数量
	int c[20] = { 0,0,0,1};//第i天杀猪的数量
	for (int i = 4; i <= 20; i++) {
		b[i] = a[i - 1];
		c[i] = b[i - 2];
		a[i] = a[i - 1] + b[i] - c[i];
	}
	int n;
	while (T) {
		cin >> n;
		cout << a[n] << endl;
		T--;
	}
	return 0;
}

分析：这个题跟前面的昆虫繁殖那个题很像，但是比那个题简单很多。我们只需知道，正道题求第i天猪的总数跟什么有关即可。

先看一张表：

第几天	1	2	3	4
猪的总数	1	2	3	5
新出生的猪	0	1	2	3
杀猪的数量	0	0	1	1

我想已经发现规律了，第i天猪的总数只跟前一天猪的总数和前两天新生猪的总数有关：

第i天猪的总数 = 前一天猪的总数 + 第i天新出生猪的总数 — 第i天杀猪的总数

其中第i天新出生猪的总数=第i-1天猪的总数

第i天杀猪的总数=前i-2天新出生猪的总数

设a[i]表示第i天晚上猪的总数，b[i]表示第i天新出生猪的总数，c[i]表示第i天杀猪的数量，则a[i]=a[i-1]+b[i]-c[i]；

b[i=a[i-1];

c[i]=b[i-2];//因为每头猪过两天生了两头猪后就要被杀。

但是这么写有问题，我们应该先算出第i天新出生猪的总数和第i天杀猪的总数，再计算，因此正确计算为：

b[i=a[i-1];

c[i]=b[i-2];

a[i]=a[i-1]+b[i]-c[i]；

通过答案发现，这个题是一个递推，f(n)=f(n-1)+f(n-2)，但是肯定不能一下子看出来，要理清题目意思，根据题目意思来计算。