索洛模型(二)
文章目录
- 索洛模型(二)
- @[toc]
- 1 事实
- 2 假设
- 2.1 对生产函数的假设
- 2.2对投入要素的假设
- 3 索洛模型的动态学
- 3.1
k
k
k的动态学
- 3.2 平衡增长路径
- 4 储蓄率变化的影响
- 4.1 对产出的影响
- 4.2 对消费的影响
文章目录
- 索洛模型(二)
- @[toc]
- 1 事实
- 2 假设
- 2.1 对生产函数的假设
- 2.2对投入要素的假设
- 3 索洛模型的动态学
- 3.1 k k k的动态学
- 3.2 平衡增长路径
- 4 储蓄率变化的影响
- 4.1 对产出的影响
- 4.2 对消费的影响
索罗经济增长模型(Solow growth model),罗伯特·索罗(Robert Solow)所提出的发展经济学中著名的模型,又称作新古典经济增长模型、外生经济增长模型,是在新古典经济学框架内的经济增长模型。
1 事实
增长奇迹:国家的增长在长期中远远高于世界平均水平,从而导致该国在世界收入分,布中的排名迅速上升。日本以及东亚新兴工业化国家和地区(简称NIC)–韩国、中国台湾、新加坡和中国香港。
增长灾难:增长灾难则是指一个国家的增长远远低于世界平均水平的现象。
一般而言,长期增长对福利的影响会超过短期波动影响,但传统宏观经济学却习惯于关注短期波动。
2 假设
四个变量:产出(
Y
Y
Y)、资本(
K
K
K)、劳动(
L
L
L)与知识或有效劳动(
L
L
L),在任意时刻
t
t
t满足
Y
(
t
)
=
F
(
K
(
t
)
,
A
(
t
)
L
(
t
)
)
(1.1)
Y(t) = F(K(t),A(t)L(t)) \tag{1.1}
Y(t)=F(K(t),A(t)L(t))(1.1)
注:这里
A
A
A与
L
L
L是以相乘的方式进入生产函数的,
A
L
AL
AL称为有效劳动,这种引入方式称为劳动增强或哈罗德中性。索罗模型的核心假设包括两个方面:
- 生成函数的假设
- 对要素投入的假设
2.1 对生产函数的假设
-
两个要素自变量(资本与有效劳动)的
规模报酬是不变的
F ( c K , c A L ) = c F ( K , A L ) , ∀ c ≥ 0 (1.2) F(cK,cAL) = cF(K,AL),\forall c \ge 0 \tag{1.2} F(cK,cAL)=cF(K,AL),∀c≥0(1.2)
这意味着经济规模足够大,使得专业分工能够的好处能最大限度利用 -
相对资本、劳动与知识来说,其他投入要素并不重要
-
索罗模型忽略土地与自然资源的作用
假定规模报酬不变的好处: 函数形式更加紧凑。在(1.2)中,令 c = 1 / A L c = 1/AL c=1/AL 得到
F
(
K
A
L
,
1
)
=
1
A
L
F
(
K
,
A
L
)
(1.3)
F(\frac{K}{AL},1) = \frac{1}{AL}F(K,AL)\tag{1.3}
F(ALK,1)=AL1F(K,AL)(1.3)
其中
K
/
A
L
K/AL
K/AL表示有效劳动平均资本量,而$ F(K,AL)/AL = Y/AL$表示单位有效劳动的平均产出。定义
Expected node of symbol group type, but got node of type cr
从而
y
=
f
(
k
)
(1.4)
y =f(k)\tag{1.4}
y=f(k)(1.4)
即把单位有效劳动平均产出写为单位有效劳动平均产出的函数。工人平均产出为
Y
L
=
A
(
Y
A
L
)
=
A
f
(
k
)
\frac{Y}{L}=A(\frac{Y}{AL})=Af(k)
LY=A(ALY)=Af(k)
函数(1.4)的经济含义是将经济体划分为
A
L
AL
AL个小经济体,每个小经济体都包含1单位有效劳动与
k
=
K
/
A
L
k =K/AL
k=K/AL单位资本,由于规模报酬不变,每个小经济体的产出都是原有经济体的
1
/
A
L
1/AL
1/AL。关于函数(1.4)还需要满足以下条件
1 资本边际产出
f
(
0
)
=
0
,
f
′
(
k
)
>
0
,
f
′
′
(
k
)
<
0
f(0)=0,f^{\prime}(k)>0,f^{\prime\prime}(k)<0
f(0)=0,f′(k)>0,f′′(k)<0
由
F
(
K
,
A
L
)
=
A
L
f
(
K
/
A
L
)
F(K,AL) = ALf(K/AL)
F(K,AL)=ALf(K/AL)可得
∂
F
(
K
,
A
L
)
∂
K
=
A
L
f
′
(
K
A
L
)
1
A
L
=
f
′
(
k
)
\frac{\partial F(K,AL) }{\partial K} = AL f^{\prime}(\frac{K}{AL})\frac{1}{AL}=f^{\prime}(k)
∂K∂F(K,AL)=ALf′(ALK)AL1=f′(k)
即要求资本的边际产出为正,且边际产出随着资本的增加而下降。
2 稻田条件
lim
k
→
0
f
′
(
k
)
=
∞
,
lim
k
→
∞
f
′
(
k
)
=
0
\mathop {\lim }\limits_{k \to 0} f^{\prime}(k) = \infty,\mathop {\lim }\limits_{k \to \infty} f^{\prime}(k) = 0
k→0limf′(k)=∞,k→∞limf′(k)=0
即当资本存量很小时,资本的边际产出非常大;当资本存量很大时,资本的边际产出非常小。其作用是保证经济路径不会发散。
例:柯布道格拉斯生产函数(Cobb-Douglas)
F
(
K
,
A
L
)
=
K
α
(
A
L
)
1
−
α
,
0
<
α
<
1
F(K,AL) =K^\alpha (AL)^{1-\alpha},0<\alpha<1
F(K,AL)=Kα(AL)1−α,0<α<1
- 规模报酬不变
F ( c K , c A L ) = c α c 1 − α K α ( A L ) 1 − α = c F ( K , A L ) F(cK,cAL) =c^\alpha c^{1-\alpha}K^\alpha (AL)^{1-\alpha}=cF(K,AL) F(cK,cAL)=cαc1−αKα(AL)1−α=cF(K,AL)
2)稻田条件
f ( k ) = F ( K A L , 1 ) = ( K A L ) α = k α f(k)=F(\frac{K}{AL},1)=(\frac{K}{AL})^{\alpha}=k^{\alpha} f(k)=F(ALK,1)=(ALK)α=kα
于是
f ′ ( k ) = α > 0 , f ′ ′ ( k ) = − ( 1 − α ) α k α − 2 < 0 f^{\prime}(k)=\alpha>0,f^{\prime\prime}(k)=-(1-\alpha)\alpha k^{\alpha-2}<0 f′(k)=α>0,f′′(k)=−(1−α)αkα−2<0
2.2对投入要素的假设
-
时间是连续的,每个变量都是关于时间的连续函数
-
资本、劳动与知识的初始值已知,并严格大于0。劳动与知识都严格按照固定比率增长
L ˙ ( t ) = n L ( t ) , A ˙ ( t ) = g A ( t ) (1.5) \dot L(t)=nL(t),\dot A(t)=gA(t)\tag{1.5} L˙(t)=nL(t),A˙(t)=gA(t)(1.5)
其中 n n n与 g g g都是外生变量。
假设经济体为两部门封闭经济,则经济总体产出
Y
Y
Y被划分为消费
C
C
C与投资
I
I
I,即
Y
=
C
+
I
=
C
+
S
Y= C+I = C+S
Y=C+I=C+S
若产出
s
s
s份额被用于投资,
(
1
−
s
)
(1-s)
(1−s)的份额用于消费,其中储蓄
s
s
s是外生给定的参数;先假设现有资本折旧率为
δ
\delta
δ,于是
K
˙
(
t
)
=
s
Y
(
t
)
−
δ
K
(
t
)
(1.6)
\dot K\left( t \right) = sY\left( t \right) - \delta K\left( t \right)\ \tag{1.6}
K˙(t)=sY(t)−δK(t) (1.6)
其中
K
˙
(
t
)
\dot K\left( t \right)
K˙(t)表示资本存量变化率,$sY\left( t \right)
为资本存量因投资而增加的数量;
为资本存量因投资而增加的数量;
为资本存量因投资而增加的数量;\delta K\left( t \right)$表示资本存量折旧而减少的数量。
3 索洛模型的动态学
3.1 k k k的动态学
经济总量会随时间不断增长,着眼于分析单位有效劳动的平均资本存量
k
k
k要比分析未经调整的资本存量
K
K
K容易得多。由
k
=
K
/
A
L
k =K/AL
k=K/AL,利用链式法则得
k
˙
(
t
)
=
K
˙
(
t
)
A
(
t
)
L
(
t
)
−
K
(
t
)
[
A
(
t
)
L
(
t
)
]
2
[
A
(
t
)
L
˙
(
t
)
+
L
(
t
)
A
˙
(
t
)
]
=
K
˙
(
t
)
A
(
t
)
L
(
t
)
−
K
(
t
)
A
(
t
)
L
(
t
)
L
˙
(
t
)
L
(
t
)
−
K
(
t
)
A
(
t
)
L
(
t
)
A
˙
(
t
)
A
(
t
)
(1.7)
\begin{aligned} \dot{k}(t) &=\frac{\dot{K}(t)}{A(t) L(t)}-\frac{K(t)}{[A(t) L(t)]^{2}}[A(t) \dot{L}(t)+L(t) \dot{A}(t)] \\ \\ &=\frac{\dot{K}(t)}{A(t) L(t)}-\frac{K(t)}{A(t) L(t)} \frac{\dot{L}(t)}{L(t)}-\frac{K(t)}{A(t) L(t)} \frac{\dot{A}(t)}{A(t)} \end{aligned} \tag{1.7}
k˙(t)=A(t)L(t)K˙(t)−[A(t)L(t)]2K(t)[A(t)L˙(t)+L(t)A˙(t)]=A(t)L(t)K˙(t)−A(t)L(t)K(t)L(t)L˙(t)−A(t)L(t)K(t)A(t)A˙(t)(1.7)
将(1.5)、(1.6)带入到(1.7)得到
k
˙
(
t
)
=
s
Y
(
t
)
−
δ
K
(
t
)
A
(
t
)
L
(
t
)
−
k
(
t
)
n
−
k
(
t
)
g
=
s
Y
(
t
)
A
(
t
)
L
(
t
)
−
δ
k
(
t
)
−
n
k
(
t
)
−
g
k
(
t
)
(1.8)
\begin{aligned} \dot{k}(t) &=\frac{s Y(t)-\delta K(t)}{A(t) L(t)}-k(t) n-k(t) g \\ \\ &=s \frac{Y(t)}{A(t) L(t)}-\delta k(t)-n k(t)-g k(t) \end{aligned} \tag{1.8}
k˙(t)=A(t)L(t)sY(t)−δK(t)−k(t)n−k(t)g=sA(t)L(t)Y(t)−δk(t)−nk(t)−gk(t)(1.8)
最后根据
f
(
k
)
=
Y
/
A
L
f(k) = Y/AL
f(k)=Y/AL得
k
˙
(
t
)
=
s
f
(
k
(
t
)
)
−
(
n
+
g
+
δ
)
k
(
t
)
(1.9)
\dot k(t) = sf(k(t))-(n+g+\delta)k(t) \tag{1.9}
k˙(t)=sf(k(t))−(n+g+δ)k(t)(1.9)
该微分方程是索洛模型得关键方程,它表明单位有效劳动平均资本存量的变化率是由以下两项之差决定的:
-
s f ( k ( t ) ) sf(k(t)) sf(k(t)):单位有效劳动的平均产出是 f ( k ) f(k) f(k),用于投资的比率为 s s s,因此该项为单位有效劳动的
实际投资 -
( n + g + δ ) k ( t ) (n+g+\delta)k(t) (n+g+δ)k(t):它代表了使得 k k k保持在现有水平所需要视为必要投资量。为防止 k k k不断减少,需要
持平投资:A A A: 现有资本会折旧,折旧部分资本必须得到资本补偿能防止资本存量下降,即 δ k ( t ) \delta k(t) δk(t)
B B B: 有效劳动的数量增加,仅保持资本存量 K K K不变的投资(补偿折旧的投资)并不足以保持单位有效劳动的平均资本存量 k k k不变。有效劳动数量增长率为 n + g n+g n+g,资本存量增长率也必须是 n + g n+g n+g才能保持 k k k不变,即 ( n + g ) k ( t ) (n+g)k(t) (n+g)k(t)
由(1.9)式可知,若
- 实际投资 > > >持平投资, k ˙ ( t ) > 0 \dot k(t) >0 k˙(t)>0,即单位有效劳动平均资本存量上升;
- 实际投资 < < <持平投资, k ˙ ( t ) < 0 \dot k(t) <0 k˙(t)<0,即单位有效劳动平均资本存量下降;
- 实际投资 = = =持平投资, k ˙ ( t ) = 0 \dot k(t) =0 k˙(t)=0,即单位有效劳动平均资本存量不变;
将实际投资与持平投资视为有效劳动平均资本 k k k的函数,其中 ( n + g + δ ) k (n+g+\delta)k (n+g+δ)k与 k k k成正比,而实际投资 s f ( k ) sf(k) sf(k)等于一个常数乘以单位有效流动平均产出。由稻田条件可知,实际投资曲线与持平投资曲线一定会在 k ≠ 0 k\ne 0 k=0之外的点 k ∗ k^* k∗出仅一次相交,用 k ∗ k^* k∗表示实际投资等于持平投资时的 k k k值。
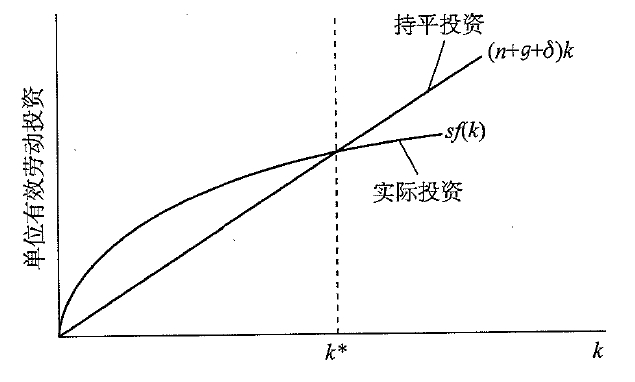
上图中, k ˙ \dot k k˙的值等于两条曲线之间的距离,将 k k k视为自变量, k ˙ \dot k k˙为因变量,于是得到关于 k k k的相位图。
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-LVxAMK5C-1684133736347)(null)]
关于相位图的解释:
- 当 k < k ∗ k< k^* k<k∗时,实际投资超过持平投资,因而 k ˙ \dot k k˙为正, k k k将不断上升;
- 当 k > k ∗ k> k^* k>k∗时,实际投资小于持平投资,因而 k ˙ \dot k k˙为负, k k k将不断下降;
- 当 k = k ∗ k = k^* k=k∗时,实际投资等于持平投资,因而 k ˙ \dot k k˙为0, k k k将保持不变,即 k ∗ k^* k∗;
因此无论 K K K位于何处,最终将会收敛到 k ∗ k^* k∗
3.2 平衡增长路径
当 k = k ∗ k = k^* k=k∗时,模型各个变量的具体变动为:
A :资本存量 K = A L k K = ALk K=ALk,由于 k = k ∗ k = k^* k=k∗,因此 K K K的增长率为 K ˙ / K = n + g \dot K/K = n+g K˙/K=n+g
B :有效劳动 A L AL AL的增长率也为( n + g n+g n+g)
C : 由于假定规模报酬不变,因此产出 Y Y Y的增长率也为 n + g n+g n+g
D: 工人平均资本 K / L K/L K/L的增长率为 g g g
E: 工人平均产出 Y / L Y/L Y/L的增长率为 g g g
证明A:
因为
K
=
A
L
k
K = ALk
K=ALk,
k
=
k
∗
k = k^*
k=k∗两边取对数得
l
n
K
=
l
n
A
+
l
n
L
+
l
n
k
lnK = ln A+lnL+lnk
lnK=lnA+lnL+lnk
同对时间求全微分
K
˙
K
=
A
˙
A
+
L
˙
L
=
g
+
n
\frac{\dot K}{K} = \frac{\dot A}{A}+ \frac{\dot L}{L} = g+n
KK˙=AA˙+LL˙=g+n
证明C:
Y
=
K
α
(
A
L
)
1
−
α
⇒
l
n
Y
=
α
l
n
K
+
(
1
−
α
)
l
n
A
+
(
1
−
α
)
l
n
L
⇒
Y
˙
Y
=
α
K
˙
K
+
(
1
−
α
)
(
L
˙
L
+
A
˙
A
)
=
α
(
n
+
g
)
+
(
1
−
α
)
(
n
+
g
)
=
n
+
g
\begin{aligned} Y& = K^\alpha(AL)^{1-\alpha} \Rightarrow lnY=\alpha lnK+(1-\alpha)lnA+(1-\alpha)lnL \\ \\ & \Rightarrow \frac{\dot Y}{Y} = \alpha\frac{\dot K}{K}+ (1-\alpha)(\frac{\dot L}{L} + \frac{\dot A}{A})= \alpha(n+g)+(1-\alpha)(n+g) =n+g \end{aligned}
Y=Kα(AL)1−α⇒lnY=αlnK+(1−α)lnA+(1−α)lnL⇒YY˙=αKK˙+(1−α)(LL˙+AA˙)=α(n+g)+(1−α)(n+g)=n+g
证明D、E:利用两个变量之比的增长率等于两个变量增长率之差得 ( n + g ) − n = g (n+g)-n = g (n+g)−n=g
因此索洛模型表明:无论初始点在何处,经济总是收敛平衡增长路径,即模型中每个变量的增长率都是常数。在平衡增长路径上,工人平均产出的增长率是由技术进步唯一确定的。
4 储蓄率变化的影响
4.1 对产出的影响
假设储蓄率 s s s永久性提高,根据公式1.9得到 k ∗ k^* k∗提高,如下图所示
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-fq587fh2-1684133736298)(null)]
下图展现了 t 0 t_0 t0时刻储蓄率变化对储蓄率 s s s,有效劳动平均资本增长率 k ˙ \dot k k˙,有效劳动平均资本 k k k,工人平均产出 Y / L Y/L Y/L和边际消费倾向 c c c的变化情况。
- 第一幅图表明储蓄率 s s s出现永久的提高
- 第二幅图由于 s s s增加导致实际投资大于持平投资,从而忽然 k ˙ > 0 \dot k>0 k˙>0,但持平投资的增长率保持不变,进而 k ˙ \dot k k˙逐渐缩小为0.
- 第三幅图由第二幅图解释。
- 第四幅图工人平均产出 Y / L = A f ( k ) Y/L = Af(k) Y/L=Af(k)的,其增长率只取决于技术进步率 g g g。随着储蓄率 s s s提高导致 k ˙ \dot k k˙短暂增加再缩小至0,因此 k k k也会增加从而 Y / L Y/L Y/L也会在 g g g的基础上提高,但后期依然取决于 g g g。第五幅图为第四幅图的对数形式
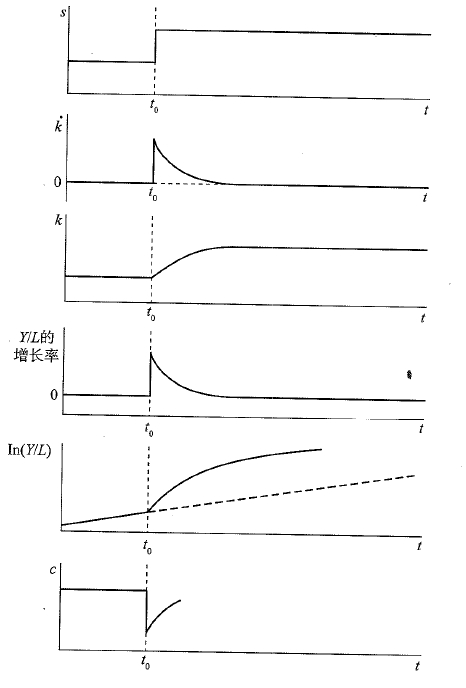
综上,储蓄率的变化只有水平效应,没有增长效应。事实上,在索洛模型中,仅有技术进步率才具有增长效应。
4.2 对消费的影响
单位有效劳动平均消费 c c c等于单位有效劳动的平均产出 f ( k ) f(k) f(k)乘以消费比例 1 − s 1-s 1−s,即 ( 1 − s ) f ( k ) (1-s)f(k) (1−s)f(k)。当储蓄率 s s s提高(阶梯式增加),而 k k k也提高(连续型增加),故 c c c出现断崖式降低,再从 t 0 t_0 t0时刻开始回升,见上第六幅图。但后期上升的幅度会超过原来的水平 c c c吗?
令
c
∗
c^*
c∗为平衡增长路径上单位有效劳动平均消费,则
c
∗
=
f
(
k
∗
)
−
(
n
+
g
+
δ
)
k
∗
c^{*} = f(k^{*})-(n+g+\delta)k^{*}
c∗=f(k∗)−(n+g+δ)k∗
因为平衡增长路径上
k
∗
=
s
f
(
k
∗
)
−
(
n
+
g
+
δ
)
k
∗
k^{*}=sf(k^*)-(n+g+\delta)k^{*}
k∗=sf(k∗)−(n+g+δ)k∗。显然
k
∗
k^{*}
k∗由
n
,
g
,
δ
n,g,\delta
n,g,δ共同决定,那么根据链式法则
∂
c
∗
∂
s
=
[
f
′
(
k
∗
(
s
,
n
,
g
,
δ
)
)
−
(
n
+
g
+
δ
)
]
∂
k
∗
(
s
,
n
,
g
,
δ
)
∂
s
\frac{\partial c^{*}}{\partial s}=\left[f^{\prime}\left(k^{*}(s, n, g, \delta)\right)-(n+g+\delta)\right] \frac{\partial k^{*}(s, n, g, \delta)}{\partial s}
∂s∂c∗=[f′(k∗(s,n,g,δ))−(n+g+δ)]∂s∂k∗(s,n,g,δ)
其中
s
s
s增加会导致
k
∗
k^{*}
k∗提高,因此储蓄率对消费的影响取决于单位有效劳动平均资本的边际产出与持平投资增长率的大小关系。
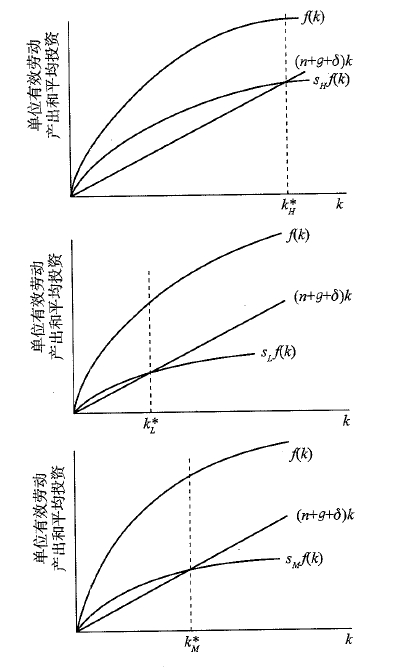
- 当 f ′ ( k ∗ ( s , n , g , δ ) ) > ( n + g + δ ) f^{\prime}\left(k^{*}(s, n, g, \delta)\right)>(n+g+\delta) f′(k∗(s,n,g,δ))>(n+g+δ)时(第一幅图),储蓄率提高促进消费增加
- 当 f ′ ( k ∗ ( s , n , g , δ ) ) < ( n + g + δ ) f^{\prime}\left(k^{*}(s, n, g, \delta)\right)<(n+g+\delta) f′(k∗(s,n,g,δ))<(n+g+δ)时(第二幅图),储蓄率提高抑制消费增加
- 当
f
′
(
k
∗
(
s
,
n
,
g
,
δ
)
)
=
(
n
+
g
+
δ
)
f^{\prime}\left(k^{*}(s, n, g, \delta)\right)=(n+g+\delta)
f′(k∗(s,n,g,δ))=(n+g+δ)时(第三幅图),储蓄率提高不对消费产生影响,但此时消费达到最大水平,此时的
k
∗
k^{*}
k∗也称为资本存量的
黄金水平。
参考文献
[美] 戴维·罗默 . 高级宏观经济学(第四版) [M]. 上海财经大学出版社,2014