内容总览
- 1.堆的定义
- 2.堆的实现接口(大堆)
- 2.1 堆结构体定义
- 2.2 堆的初始化与销毁
- 2.3 堆的向上调整算法和插入
- 2.4 堆的向下调整算法和删除堆顶元素
- 2.5 堆的其他接口(调整堆递归版本)
- 3.建堆效率问题分析
- 3.1 向上建堆
- 3.2 向下建堆
- 4. 堆排序(升序)
- 5.TopK问题分析
1.堆的定义
堆是以二叉树的结构方式,所存储的一维数组。
逻辑结构:二叉树
物理结构:一维数组
堆的特性:
- 堆中某个节点的值总是不大于或不小于它的父亲节点的值。根结点值总是大于或等于其左右孩子结点的值,叫大根堆。根节点总是小于或等于其左右孩子结点的值,叫小根堆。
- 堆总是一棵完全二叉树。
如下图堆的示例:

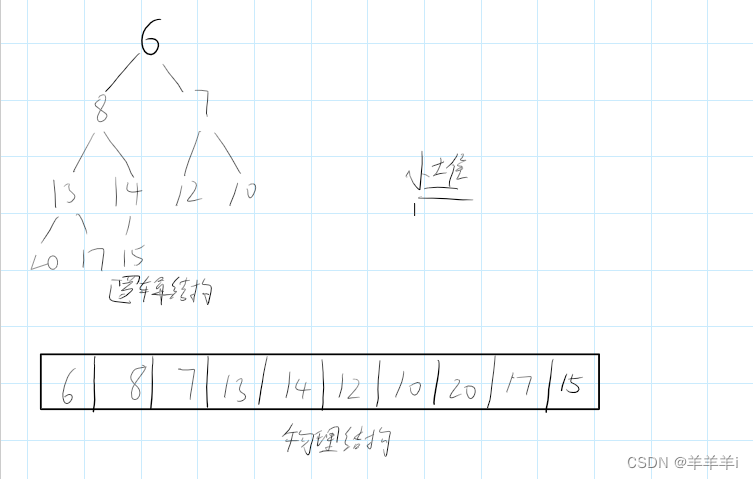
2.堆的实现接口(大堆)
2.1 堆结构体定义
使用一维数组来存储堆
typedef int HPDataType;
typedef struct Heap
{
HPDataType* data;
int size;
int capacity;
}Heap;
2.2 堆的初始化与销毁
//堆初始化
void HeapInit(Heap* pa)
{
assert(pa);
pa->data = NULL;
pa->capacity = pa->size = 0;
}
//销毁堆
void HeapDestroy(Heap* pa)
{
assert(pa);
free(pa->data);
pa->data = NULL;
pa->capacity = pa->size = 0;
}
2.3 堆的向上调整算法和插入
堆进行插入的时候,接口是进行尾插的,这样能保证不会破坏之前的堆的结构。插入过程大概如下步骤:假设输入数据为:

算法思想:由需要调整的结点开始,把它当作孩子结点child。计算出父亲节点parent,将孩子和父亲的值作比较,如果父亲小于孩子,择交换两结点的值。并且令child = parent.一直重复,直到调整到根结点为止。
//向上调整
void AdjustUp(HPDataType* a, int child)
{
int parent = (child - 1) / 2;
while (child > 0)
{
//不符合堆定义
if (a[child] > a[parent])
{
Swap(&a[child], &a[parent]);
child = parent;
parent = (child - 1) / 2;
}
//符合堆定义
else
{
break;
}
}
}
//堆插入(大堆)
void HeapPush(Heap* pa, HPDataType x)
{
assert(pa);
//检查容量
if (pa->size == pa->capacity)
{
int newcapacity = (pa->capacity == 0 ? 4 : pa->capacity * 2);
HPDataType* tem = (HPDataType*)realloc(pa->data, sizeof(HPDataType) * newcapacity);
//申请失败,终止程序
if (tem == NULL)
{
perror("realloc failed");
exit(-1);
}
pa->data = tem;
pa->capacity = newcapacity;
}
//插入数据
pa->data[pa->size] = x;
pa->size++;
//向上调整
AdjustUp(pa->data,pa->size-1);
}
2.4 堆的向下调整算法和删除堆顶元素
堆进行删除时候,不能直接删除堆顶元素,这样会把数据整体前移,破坏了堆的结构。规定:把堆顶元素和最后一个元素交换。然后将size-1,就可完成删除任务。只需利用向下调整算法,就能在O(logN)的时间内完成恢复堆的任务。
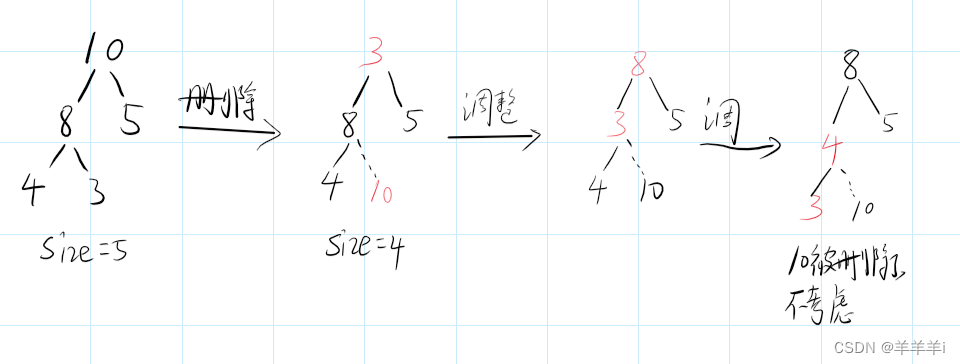
算法思想:从堆顶元素开始向下调整,首先比较两个孩子结点,找出较大的结点。与父亲节点比较,若孩子结点的值小于父亲结点的值,则说明符合堆的结构,调整完成。否则将父亲结点和孩子结点的值交换,并且令parent = child(继续向下调整),直到符合堆结构或者没有叶子结点,调整完成。
//向下调整
void AdjustDown(HPDataType* a, int size, int parent)
{
int child = 2 * parent + 1; //左孩子下标
//如果有孩子,必须小于size
while (child < size)
{
//选出较大的孩子(右孩子不能超出范围)
if (child + 1 < size && a[child + 1] < a[child])
{
child++;
}
//孩子大于父亲就交换,不大于就退出
if (a[child] < a[parent])
{
Swap(&a[child], &a[parent]);
parent = child;
child = parent * 2 + 1;
}
else
{
break;
}
}
}
//堆删除
void HeapPop(Heap* pa)
{
assert(pa);
assert(pa->size > 0);
//换到最低层
Swap(&(pa->data[0]), &(pa->data[pa->size-1]));
pa->size--;
//向下调整
AdjustDown(pa->data,pa->size,0);
}
2.5 堆的其他接口(调整堆递归版本)
//获取堆顶元素
HPDataType HeapTop(Heap* pa)
{
assert(pa);
assert(pa->size > 0);
return pa->data[0];
}
//堆的数据个数
int HeapSize(Heap* pa)
{
assert(pa);
return pa->size;
}
//堆的判空
bool HeapEmpty(Heap* pa)
{
assert(pa);
if (pa->size > 0)
{
return false;
}
return true;
}
//向上调整(递归版本)
void AdjustUp(HPDataType* a, int child)
{
int parent = (child - 1) / 2;
if(child > 0)
{
//不符合堆定义
if (a[child] > a[parent])
{
Swap(&a[child], &a[parent]);
AdjustUp(a, parent); //把父亲当作儿子传进去
}
}
}
//向下调整(递归版本)
void AdjustDown(HPDataType* a, int size, int parent)
{
int child = 2 * parent + 1; //左孩子下标
//如果有孩子,必须小于size
if (child < size)
{
//选出较大的孩子(右孩子不能超出范围)
if (child + 1 < size && a[child + 1] > a[child])
{
child++;
}
//孩子大于父亲就交换,不大于就退出
if (a[child] > a[parent])
{
Swap(&a[child], &a[parent]);
AdjustDown(a, size, child); //把孩子当成父亲传进去
}
}
}
3.建堆效率问题分析
3.1 向上建堆
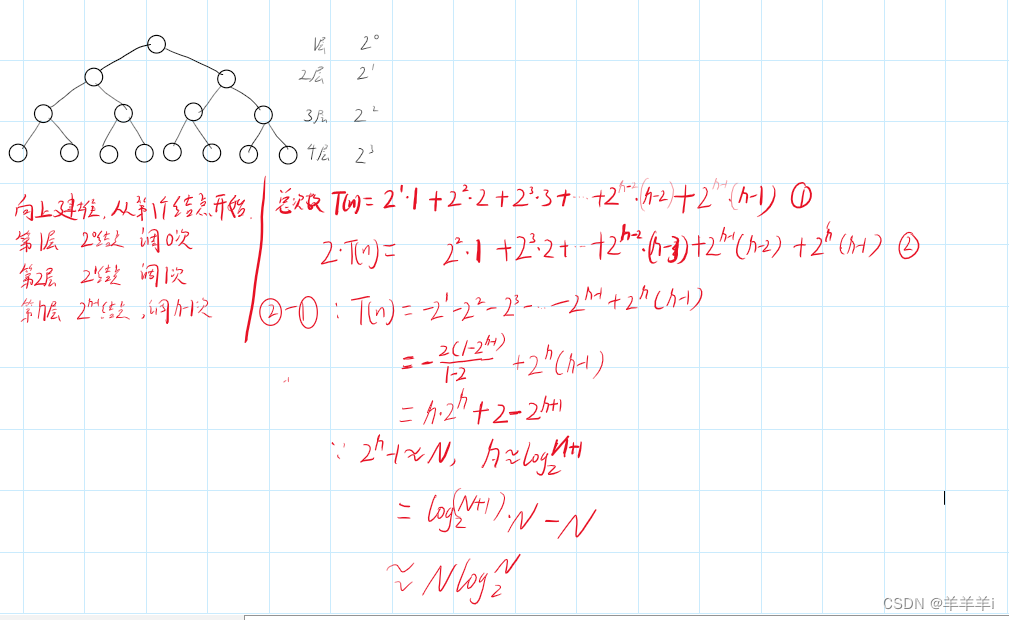
因此向上建堆的时间复杂度为O(NlogN)。
3.2 向下建堆

因此向下建堆的时间复杂度为O(N)。
4. 堆排序(升序)
- 利用堆的Top和Pop接口来实现排序,但是需要申请空间来保存Pop之后的数据。并且每次都需要实现堆的接口比较麻烦。
- 利用Pop的思想,将最大的元素和最后一个元素互换。每次交换size–,不断循环这个动作,直到size大小为0。
本文采用第二种方法:
//升序
void HeapSort(HPDataType* a, int size)
{
//先建堆
for (int i = (size - 1 - 1) / 2; i >= 0; i--)
{
//向下调整(从后往前)
AdjustDown(a, size, i);
}
//再一个一个调整
int end = size - 1; //记录堆的最后一个位置
while (end > 0)
{
//第一个和最后一个位置交换
Swap(&a[0], &a[end]);
//向下调整
AdjustDown(a, end, 0);
end--;
}
}
分析:第一部分向下建堆时间复杂度为0(N),堆排序的时间复杂度为O(NlogN)。
综上:堆排序的时间复杂度为O(NlogN)。
5.TopK问题分析
题目背景:要求找出100万个数字里最大的前10个数。
方法1:
建立N个数的大根堆,每次找出最大的数字,重复10次即可。但是空间效率极高。
时间复杂度O(N+KlogN)。
方法2:
建立K个数字的小根堆,依次遍历剩下数据,如果数值大于堆顶数据,则进堆,如果数值小于堆顶数据,则跳过。遍历完,堆中的数据就是最大的前10个。
时间复杂度O(K+(N-K)logK)。
方法2的效率更高一点,且占用空间小:
//找前K个最大的数字
void PrintTopK(int* a, int size, int K)
{
int* tem = (int*)malloc(sizeof(int) * K);
assert(tem);
//建立前K个数字的小堆
for (int i = 0; i < K; i++)
{
tem[i] = a[i];
if (tem == NULL)
{
exit(-1);
}
AdjustUp(tem, i);
}
//剩下的数字依次和堆顶元素比较
int j = K;
while (j < size)
{
if (a[j] >= tem[0])
{
tem[0] = a[j];
AdjustDown(tem, K, 0);
}
j++;
}
for (int i = 0; i < K; i++)
{
printf("%d ", tem[i]);
}
}
总结:以上就是堆相关的问题介绍,后续还会继续更新数据结构相关的知识。敬请期待。💞