张量分量的变换定律
张量的分量是依赖于坐标系的,所以当坐标系发生旋转,张量分量也会发生改变,张量分量与坐标系通过分量变换规律互相关联起来的。
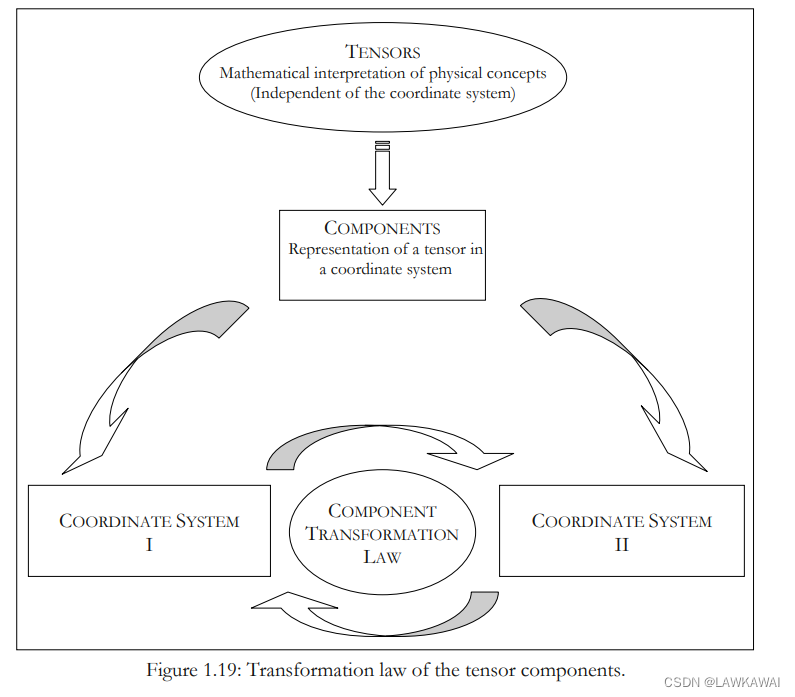
考虑在正交基
(
e
^
1
,
e
^
2
,
e
^
3
)
(\hat e_1, \hat e_2, \hat e_3)
(e^1,e^2,e^3)的坐标系
(
x
1
,
x
2
,
x
3
)
(x_1, x_2, x_3)
(x1,x2,x3),任意向量可以表示成:
v
⃗
=
v
i
e
^
i
=
v
1
e
^
1
+
v
2
e
^
2
+
v
3
e
^
3
\vec v = v_i\hat e_i = v_1\hat e_1 + v_2\hat e_2 + v_3\hat e_3
v=vie^i=v1e^1+v2e^2+v3e^3
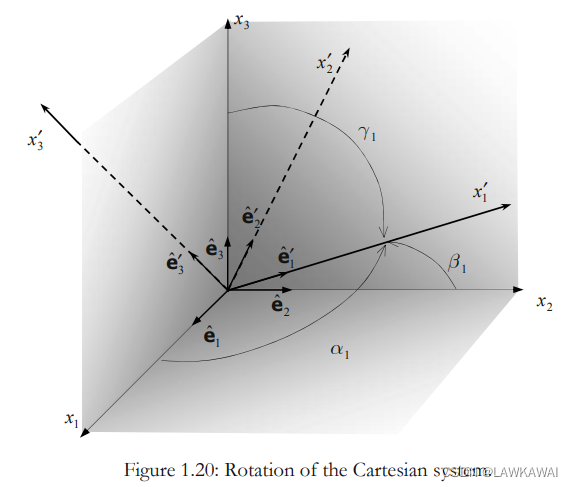
矩阵形式:
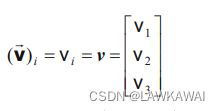
考虑一个新的坐标系
(
x
1
′
,
x
2
′
,
x
3
′
)
(x_1', x_2', x_3')
(x1′,x2′,x3′), 基于正交基
(
e
^
1
′
,
e
^
2
′
,
e
^
3
′
)
(\hat e_1', \hat e_2', \hat e_3')
(e^1′,e^2′,e^3′),在这个新的坐标系种,向量可以表示成
v
⃗
=
v
j
′
e
^
j
′
\vec v = v'_j \hat e_j'
v=vj′e^j′, 所以:
v
⃗
=
v
k
′
e
^
k
′
=
v
j
e
^
j
\vec v = v_k'\hat e_k' = v_j \hat e_j
v=vk′e^k′=vje^j
为了计算得到在某个坐标系的张量的分量,只需要将张量和坐标基进行点积即可:
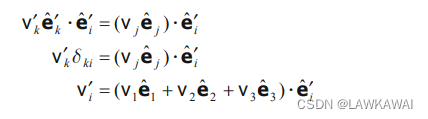
或者矩阵形式:
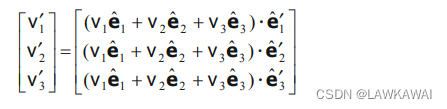

所以,坐标变换张量的分量的计算公式:
a
i
j
=
e
^
j
⋅
e
^
i
′
=
e
^
i
′
⋅
e
^
j
a_{ij} = \hat e_j \cdot \hat e_i' = \hat e_i' \cdot \hat e_j
aij=e^j⋅e^i′=e^i′⋅e^j
指标形式:
v
i
′
=
a
i
j
v
j
\boxed{v_i'= a_{ij}v_j}
vi′=aijvj
坐标变换矩阵:张量在原坐标系变换到新坐标系的变换矩阵,新坐标基控制矩阵的行
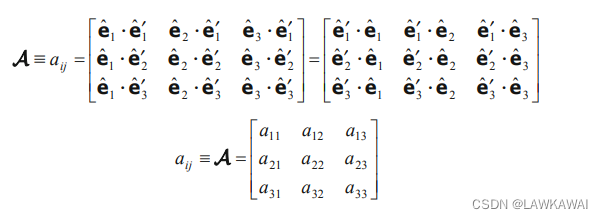
矩阵不是对称的
由于
e
^
i
′
⋅
e
^
j
=
∣
∣
e
^
i
′
∣
∣
∣
∣
e
^
j
∣
∣
cos
(
x
i
′
,
x
j
)
\hat e_i' \cdot \hat e_j = ||\hat e_i'|| ||\hat e_j|| \cos(x_i', x_j)
e^i′⋅e^j=∣∣e^i′∣∣∣∣e^j∣∣cos(xi′,xj),所以可以把变换矩阵表示成方向余弦的形式:
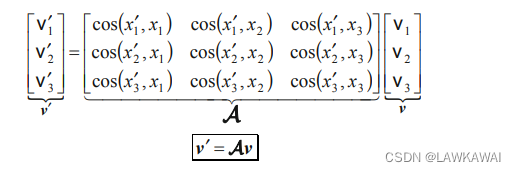
方向余弦的角度是向量与原坐标系的角度
cos
α
1
=
cos
(
x
1
′
,
x
1
)
\cos \alpha_1 = \cos (x_1', x_1)
cosα1=cos(x1′,x1)
cos
β
1
=
cos
(
x
1
′
,
x
2
)
\cos \beta _1= \cos (x_1', x_2)
cosβ1=cos(x1′,x2)
cos
γ
1
=
cos
(
x
1
′
,
x
3
)
\cos \gamma_1 = \cos (x_1', x_3)
cosγ1=cos(x1′,x3)

上面已经讨论了向量在新坐标系的投影,下面是向量在原坐标系的投影:
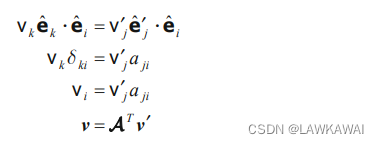
因此:
e
^
i
=
a
j
i
e
^
j
′
\boxed{\hat e_i = a_{ji} \hat e_{j}'}
e^i=ajie^j′
逆变换矩阵:
A
−
1
v
⃗
′
=
A
−
1
A
v
⃗
⟹
v
=
A
−
1
v
⃗
′
A^{-1}\vec v' = A^{-1}A \vec v \implies v = A^{-1}\vec v'
A−1v′=A−1Av⟹v=A−1v′
由于 v = A − 1 v ⃗ ′ v = A^{-1}\vec v' v=A−1v′ 且 v ⃗ = A T v ⃗ ′ \vec v = A^T \vec v' v=ATv′,可以得出 A A A 是正交矩阵:
A − 1 = A T ⟹ A T A = 1 → a k i a k j = δ i j A^{-1} = A^T \implies A^T A = 1 \rightarrow a_{ki}a_{kj} = \delta_{ij} A−1=AT⟹ATA=1→akiakj=δij
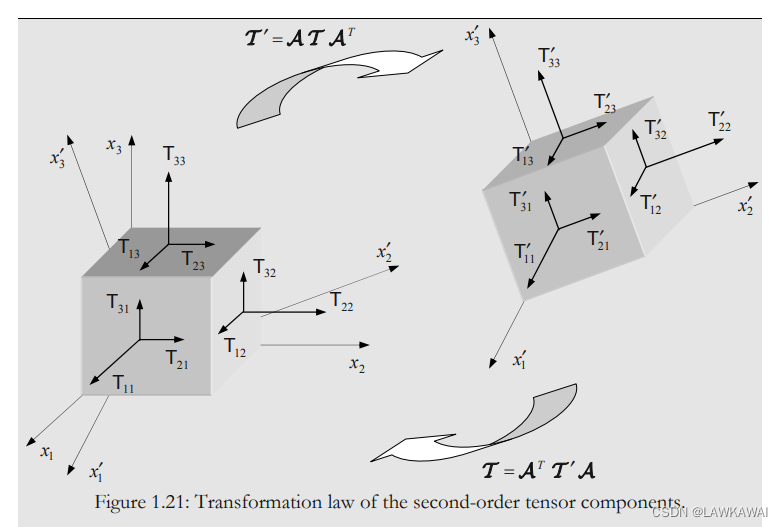
二阶张量:
从原坐标系的正交基
e
^
i
\hat e_i
e^i 变换到新坐标系得正交基
e
^
i
′
\hat e_i'
e^i′,遵循变换定律:
e
^
k
=
a
i
k
e
^
i
′
\hat e_k = a_{ik} \hat e_i'
e^k=aike^i′
这可以将二阶张量表示为:

其中:
T
i
j
′
=
T
k
l
a
i
k
a
j
l
=
a
i
k
T
k
l
a
j
l
→
T
′
=
A
T
A
′
T_{ij}' = T_{kl}a_{ik}a_{jl}=a_{ik}T_{kl}a_{jl} \rightarrow T' = A T A'
Tij′=Tklaikajl=aikTklajl→T′=ATA′
三阶张量:
可以将三阶张量表示为正交基
e
^
i
\hat e_i
e^i 和正交基
e
^
i
′
\hat e_i'
e^i′:
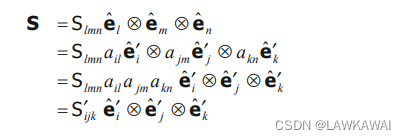
所以,三阶张量在新正交基的分量:
S
i
j
k
′
=
S
l
m
n
a
i
l
a
j
m
a
k
n
S'_{ijk} = S_{lmn}a_{il}a_{jm}a_{kn}
Sijk′=Slmnailajmakn
根据张量阶数总结变换定律:

问题1.27 给定 T ′ = A ⋅ T ⋅ A ′ T' = A \cdot T \cdot A' T′=A⋅T⋅A′, 计算 T ′ T' T′的分量
思路: 先将其转换成指标形式,然后为了求二阶张量的分量表示,需要同时作用双缩并
:
(
e
^
i
⨂
e
^
j
)
:(\hat e_i \bigotimes \hat e_j)
:(e^i⨂e^j)

问题1.128 T T T是一个对称二阶张量, I T , I I T , I I I T I_T, II_T, III_T IT,IIT,IIIT是标量,其中 I T = T r ( T ) = T i i , I I T = 1 2 [ I T 2 − T r ( T 2 ) ] , I I I T = det T I_T = Tr(T) = T_{ii}, \quad II_T = \frac{1}{2}[I_T^2-Tr(T^2)], \quad III_T = \det T IT=Tr(T)=Tii,IIT=21[IT2−Tr(T2)],IIIT=detT, 证明 I T , I I T , I I I T I_T, II_T, III_T IT,IIT,IIIT是做坐标基变换的不变量

其中,用到正交张量的定义:
由于A是正交张量,所以有:
a
i
k
a
i
l
=
δ
k
l
→
A
⋅
A
T
=
1
a_{ik}a_{il} = \delta_{kl} \rightarrow A\cdot A^T = 1
aikail=δkl→A⋅AT=1
其中,还用到张量的迹:
A
:
B
=
T
r
(
A
⋅
B
T
)
A:B = Tr(A \cdot B^T)
A:B=Tr(A⋅BT)
由于
T
′
T'
T′ 是正交张量,所以
T
′
=
(
T
′
)
T
T' = (T')^T
T′=(T′)T,所以
T
r
(
T
′
⋅
T
′
)
=
T
r
(
T
′
⋅
(
T
′
)
T
)
=
T
′
:
T
′
Tr(T' \cdot T') = Tr(T' \cdot (T')^T) = T' : T'
Tr(T′⋅T′)=Tr(T′⋅(T′)T)=T′:T′
所以,目前提到了三个不变量:
张量的迹;
张量的迹的平方 - 张量平方的迹;
张量的行列式
有四个坐标系:
(
x
1
,
x
2
,
x
3
)
(x_1, x_2, x_3)
(x1,x2,x3)
(
x
1
′
,
x
2
′
,
x
3
′
)
(x_1', x_2', x_3')
(x1′,x2′,x3′)
(
x
1
′
′
,
x
2
′
′
,
x
3
′
′
)
(x_1'', x_2'', x_3'')
(x1′′,x2′′,x3′′)
(
x
1
′
′
′
,
x
2
′
′
′
,
x
3
′
′
′
)
(x_1''', x_2''', x_3''')
(x1′′′,x2′′′,x3′′′)
考虑以下变换矩阵:
A
A
A: 从
(
x
1
,
x
2
,
x
3
)
(x_1, x_2, x_3)
(x1,x2,x3) 变换到
(
x
1
′
,
x
2
′
,
x
3
′
)
(x_1', x_2', x_3')
(x1′,x2′,x3′)
B
B
B: 从
(
x
1
′
,
x
2
′
,
x
3
′
)
(x_1', x_2', x_3')
(x1′,x2′,x3′) 变换到
(
x
1
′
′
,
x
2
′
′
,
x
3
′
′
)
(x_1'', x_2'', x_3'')
(x1′′,x2′′,x3′′)
C: 从
(
x
1
′
′
,
x
2
′
′
,
x
3
′
′
)
(x_1'', x_2'', x_3'')
(x1′′,x2′′,x3′′) 变换到
(
x
1
′
′
′
,
x
2
′
′
′
,
x
3
′
′
′
)
(x_1''', x_2''', x_3''')
(x1′′′,x2′′′,x3′′′)
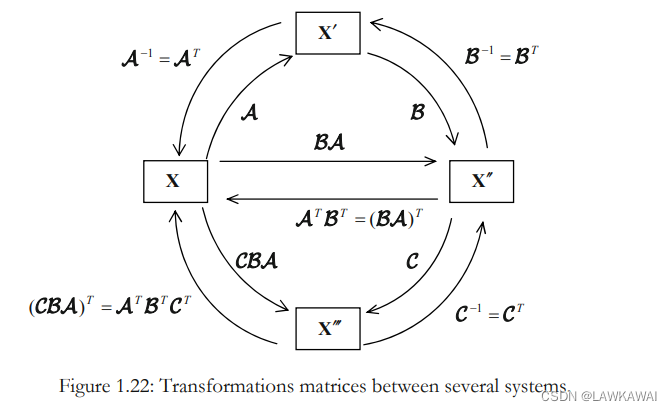
如果有一个向量
v
⃗
\vec v
v, 在每个坐标系之间的转换如下所示:
从
(
x
1
,
x
2
,
x
3
)
(x_1, x_2, x_3)
(x1,x2,x3) 变换到
(
x
1
′
,
x
2
′
,
x
3
′
)
(x_1', x_2', x_3')
(x1′,x2′,x3′):
v
⃗
′
=
A
v
⃗
\vec v' = A\vec v
v′=Av
从
(
x
1
′
,
x
2
′
,
x
3
′
)
(x_1', x_2', x_3')
(x1′,x2′,x3′) 变换到
(
x
1
,
x
2
,
x
3
)
(x_1, x_2, x_3)
(x1,x2,x3):
v
⃗
=
A
T
v
⃗
′
\vec v = A^T\vec v'
v=ATv′
从
(
x
1
′
,
x
2
′
,
x
3
′
)
(x_1', x_2', x_3')
(x1′,x2′,x3′) 变换到
(
x
1
′
′
,
x
2
′
′
,
x
3
′
′
)
(x_1'', x_2'', x_3'')
(x1′′,x2′′,x3′′):
v
⃗
′
′
=
B
v
⃗
′
\vec v'' = B \vec v'
v′′=Bv′
从
(
x
1
′
′
,
x
2
′
′
,
x
3
′
′
)
(x_1'', x_2'', x_3'')
(x1′′,x2′′,x3′′)变换到
(
x
1
′
,
x
2
′
,
x
3
′
)
(x_1', x_2', x_3')
(x1′,x2′,x3′) :
v
⃗
′
=
B
T
v
⃗
′
′
\vec v' = B^T \vec v''
v′=BTv′′
代入
v
⃗
′
=
A
v
⃗
\vec v' = A\vec v
v′=Av, 从
(
x
1
,
x
2
,
x
3
)
(x_1, x_2, x_3)
(x1,x2,x3) 变换到
(
x
1
′
′
,
x
2
′
′
,
x
3
′
′
)
(x_1'', x_2'', x_3'')
(x1′′,x2′′,x3′′) :
v
⃗
′
′
=
B
v
⃗
′
=
B
A
v
⃗
\vec v'' = B \vec v' = BA\vec v
v′′=Bv′=BAv
从
(
x
1
′
′
,
x
2
′
′
,
x
3
′
′
)
(x_1'', x_2'', x_3'')
(x1′′,x2′′,x3′′) 变换到
(
x
1
,
x
2
,
x
3
)
(x_1, x_2, x_3)
(x1,x2,x3) :
v
⃗
=
A
T
B
T
v
⃗
′
′
\vec v = A^T B^T\vec v''
v=ATBTv′′
从
(
x
1
,
x
2
,
x
3
)
(x_1, x_2, x_3)
(x1,x2,x3) 变换到
(
x
1
′
′
′
,
x
2
′
′
′
,
x
3
′
′
′
)
(x_1''', x_2''', x_3''')
(x1′′′,x2′′′,x3′′′) :
v
⃗
′
′
′
=
C
B
A
v
⃗
\vec v''' = CBA\vec v
v′′′=CBAv
从
(
x
1
′
′
′
,
x
2
′
′
′
,
x
3
′
′
′
)
(x_1''', x_2''', x_3''')
(x1′′′,x2′′′,x3′′′)变换到
(
x
1
,
x
2
,
x
3
)
(x_1, x_2, x_3)
(x1,x2,x3) :
v
⃗
=
A
T
B
T
C
T
v
⃗
′
′
′
\vec v = A^TB^TC^T\vec v'''
v=ATBTCTv′′′
二维分量变换定律
考虑两个坐标系:
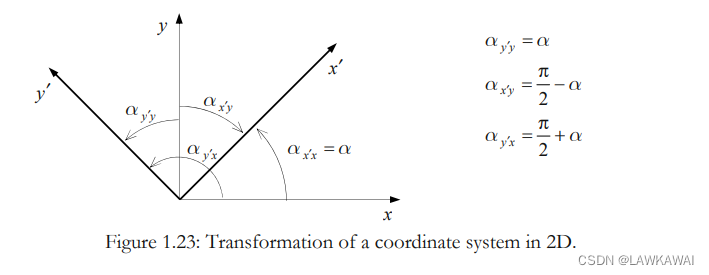
从(x, y) 到(x’, y’):
v
⃗
′
=
A
v
⃗
\vec v' = A\vec v
v′=Av
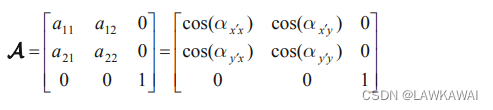
利用三角恒等式:
α
x
′
x
=
α
y
′
y
⟹
cos
(
α
x
′
x
)
=
cos
(
α
y
′
y
)
=
cos
(
α
)
cos
(
α
x
′
y
)
=
cos
(
π
2
−
α
)
=
sin
(
α
)
cos
(
α
y
′
x
)
=
cos
(
π
2
+
α
)
=
−
sin
(
α
)
\alpha_{x'x}=\alpha_{y'y} \implies \cos(\alpha_{x'x}) = \cos(\alpha_{y'y})=\cos(\alpha) \\ \cos(\alpha_{x'y}) = \cos(\frac{\pi}{2}-\alpha) = \sin(\alpha) \\ \cos(\alpha_{y'x}) = \cos(\frac{\pi}{2}+\alpha) = -\sin(\alpha)
αx′x=αy′y⟹cos(αx′x)=cos(αy′y)=cos(α)cos(αx′y)=cos(2π−α)=sin(α)cos(αy′x)=cos(2π+α)=−sin(α)
所以,二维的变换矩阵:
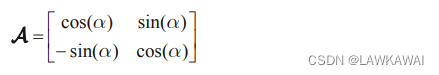
另一个证明方法:
考虑在两个坐标系的一个点P的向量方向:
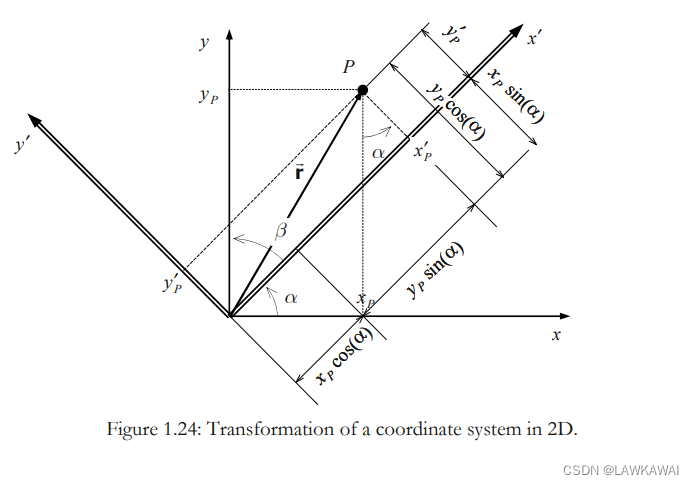
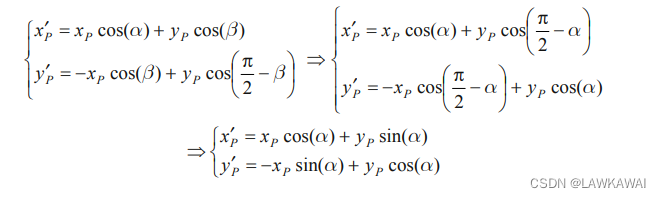
矩阵形式:

又因为
A
−
1
=
A
A^{-1} = A
A−1=A, 所以:
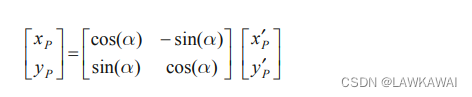
问题1.29 求出坐标系 ( x , y , z ) (x, y, z) (x,y,z)和 ( x ′ ′ ′ , y ′ ′ ′ , z ′ ′ ′ ) (x''', y''', z''') (x′′′,y′′′,z′′′)之间的变换矩阵




α
,
β
,
γ
\alpha, \beta, \gamma
α,β,γ 是欧拉角,用来计算刚体运动的方向
问题1.30 T T T是二阶张量

NOTE: 以上例子可以看出,张量
T
T
T 在新坐标基的分量有一个特性, 非对角元素是零,现在问题是:给定任意一个张量
T
T
T ,是否存在使得非对角元素为零的变换?
这种问题的类型是特征值问题。
参考教材:
Eduardo W.V. Chaves, Notes On Continuum Mechanics