进一步了解傅里叶变换的应用（附案例代码）

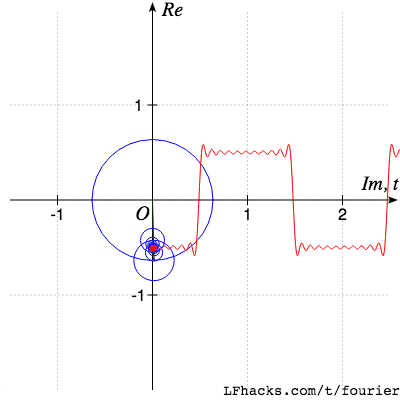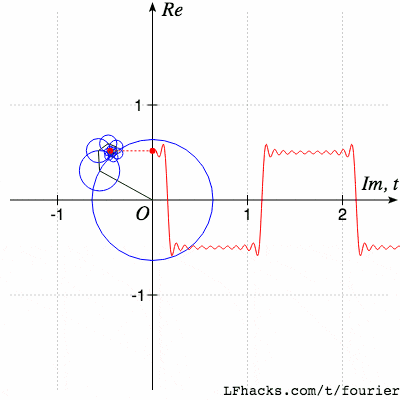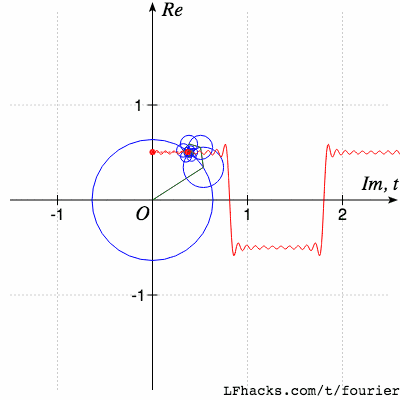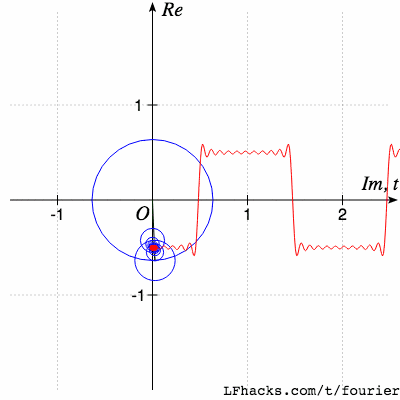
傅里叶变换（Fourier Transform）是一种非常常见的数学工具，能够将一个函数（或时域信号）分解成一些基本频率的合成。它使我们可以将时域信号（例如波形图）转换成频域信号，因而更容易地看出信号中的频率成分。傅里叶变换的基本思想是将一个连续信号分解成一些正弦波（即基本频率）的加权和，即任意周期信号都能表示成单频正弦函数或余弦函数的和的形式，这些正弦波的频率、振幅和相位可以表征原信号的特征。傅里叶变换可以在频域上对信号进行分析，以便检测特定频率的信号成分，因此常被用于信号处理、通信和图像处理等领域。值得注意的是，傅里叶变换不仅可以对连续信号进行转换，还可以对离散信号（如数字信号）进行离散傅里叶变换（DFT）处理。

1、实现图像增强

通过傅里叶变换将图像转化为频域，并进行滤波操作，从而去除噪声和干扰，提高图像质量。使用傅里叶变换（FFT）进行图像增强通常涉及以下步骤：

将图像转换成频域：将图像进行二维傅里叶变换得到其频谱数据；
可选滤波：对频谱数据进行滤波，可以去除一些不需要的频率，并保留一些需要增强的频率；
将频谱转换回空域：使用傅里叶逆变换将带有滤波后的增强信息的频谱转换回空域；
对输出进行增强：将增强后的图像与原始图像进行比较。如果需要进一步增强图像，可以进行适当的调整。

在实际操作时，还需要考虑如何选择适当的滤波算法以及如何调整滤波后的频域数据以达到最佳的图像增强效果。常用的滤波算法有低通滤波、高通滤波、带通滤波、陷波和同态滤波等。选择使用哪种滤波算法应根据不同场景进行具体分析。

2、图像压缩

使用傅里叶变换将图像转化为频域表示，在频域中进行压缩处理，通过舍弃低振幅的高频成分实现图像压缩和数据存储的减少。傅里叶变换进行图像压缩通常包括以下步骤：

将图像转换为频域：通过使用二维离散傅里叶变换（DFT）将图像从空域转换到频域，得到其频谱数据；
压缩频域数据：可以采用不同的压缩算法，如使用奇异值分解（SVD）的压缩，使用小波变换进行压缩等方式对得到的频谱数据进行压缩；
将压缩后的频域数据转换回空域：通过使用离散傅里叶逆变换（IDFT）可以将压缩后的频域数据转换回空域；
进一步数据压缩：可应用各种数据压缩算法来增强所获得的数据压缩效果。

需要注意的是，将图像转换为频域会导致周围无用的零频项出现，而这些零频项在压缩的过程中对于数据压缩是有害的，会导致数据压缩的效果不如预期。因此，在对图像进行傅里叶变换之前，必须首先对其进行零填充来扩展图像，使其的大小具有固定的形式。此外，傅里叶变换还对图像的对齐和旋转引起的问题敏感。

3、图像分析

傅里叶变换能够将图像中的纹理和周期性变化分解出来，进而进行特征提取和分析。比如可以通过傅里叶变换来检测和分析图像中的纹理特征。傅里叶变换进行图像分析通常包括以下步骤：

将图像转换为频域：通过使用二维离散傅里叶变换（DFT）将图像从空域转换到频域，得到其频谱数据；
分析频域数据：我们可以分析得到的频域数据来提取图像的各种属性，如频率谱、图像的峰值、频域滤波器等等；
将频域数据转换回空域：通过使用离散傅里叶逆变换（IDFT）可以将分析后的频域数据转换回空域；
观察分析结果：通过观察分析后得到的结果可得到图像各种属性的分布情况以及与其他图像的比较结果等。

在使用傅里叶变换进行图像分析时，频域数据的分析需要根据具体的应用需求来进行。例如，我们可以观察图像的频率谱来判断图像中的高频或低频信号，也可以使用频域滤波器来去除图像中的噪声。此外，由于傅里叶变换基于局部均衡性的假设，因此分析结果可能会受到光照、投影等因素的影响。因此，在实际运用中需要选用合适的算法来减少这些因素的影响，并且需要根据具体情况来进行调整和优化。

4、图像重建

傅里叶变换实现图像重建的具体步骤如下：

选择一张需要重建的图像，并进行离散化。一般可以将图像划分为像素并将像素的灰度值转换为矩阵；
对图像矩阵进行二维离散傅里叶变换（DFT），得到频谱数据；
根据需要，可以使用滤波器对频谱数据进行处理以去除噪声或其他干扰信号。比如，可以使用高通/低通滤波器进行滤波操作；
对经过滤波处理的频谱数据进行逆变换，得到重建后的图像；
可以对重建后的图像进行分析和评估，比如进行对比度和清晰度的测量。

需要注意的是，图像重建过程中可能会出现信息丢失，因此在滤波或其他后处理中需要慎重考虑。此外，傅里叶变换常常要求进行矩阵计算，因此计算机的计算速度和计算精度也会影响图像重建的准确度，建议结合深度学习等热点方向使用。

5、案例代码实现（基于python+openCV）

（1）导入相关模块和原始图像

import numpy as np
import matplotlib.pyplot as plt
import cv2

img = cv2.imread('imageslion.jpg', 0)

img

输出结果：

rows, cols = img.shape
print(rows, cols)

输出结果：
281 282

第一次运行，可能会出现如下情况：

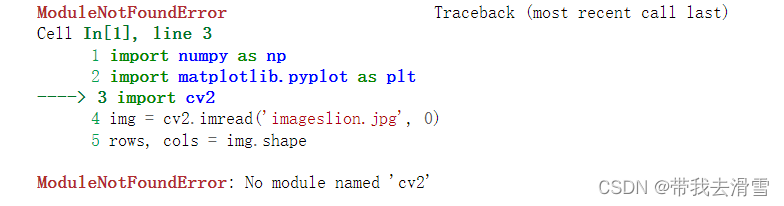
打开Anaconda Prompt，运行pip install opencv-python，或者pip install opencv-python-headless，解决 cv2 安装失败的问题。

（2）计算DFT效率最佳的尺寸

nrows = cv2.getOptimalDFTSize(rows)
ncols = cv2.getOptimalDFTSize(cols)
print(nrows, ncols)
输出结果：
288 288
nimg = np.zeros((nrows, ncols))
nimg[:rows, :cols] = img
img = nimg

img

输出结果：
array([[  1.,   4.,   1., ...,   0.,   0.,   0.],
       [ 57., 109., 116., ...,   0.,   0.,   0.],
       [ 69., 157., 160., ...,   0.,   0.,   0.],
       ...,
       [  0.,   0.,   0., ...,   0.,   0.,   0.],
       [  0.,   0.,   0., ...,   0.,   0.,   0.],
       [  0.,   0.,   0., ...,   0.,   0.,   0.]])

（3）将图像转换为np.float32，然后使用函数cv2.dft()和cv2.idft()

dft = cv2.dft(np.float32(img), flags=cv2.DFT_COMPLEX_OUTPUT)
dft_shift = np.fft.fftshift(dft)

magnitude_spectrum = 20 * np.log(cv2.magnitude(dft_shift[:, :, 0], dft_shift[:, :, 1]))

plt.subplot(221), plt.imshow(img, cmap='gray')
plt.title('Input Image'), plt.xticks([]), plt.yticks([])
plt.subplot(222), plt.imshow(magnitude_spectrum, cmap='gray')
plt.title('Magnitude Spectrum'), plt.xticks([]), plt.yticks([])

rows, cols = img.shape
crow, ccol = rows // 2, cols // 2

# 首先创建一个mask，中心正方形为1，其他均为0
# 如何删除图像中的高频内容:将LPF应用于图像。它实际上模糊了图像。
# 为此首先创建一个在低频时具有高值的掩码，即传递LF内容，在HF区域为0。
mask = np.zeros((rows, cols, 2), np.uint8)
mask[crow - 30:crow + 30, ccol - 30:ccol + 30] = 1

（4）应用掩码Mask和求逆DTF

fshift = dft_shift * mask
f_ishift = np.fft.ifftshift(fshift)
img_back = cv2.idft(f_ishift)
img_back = cv2.magnitude(img_back[:, :, 0], img_back[:, :, 1])

plt.subplot(223), plt.imshow(img, cmap='gray')
plt.title('Input Image'), plt.xticks([]), plt.yticks([])
plt.subplot(224), plt.imshow(img_back, cmap='gray')
plt.title('Magnitude Spectrum'), plt.xticks([]), plt.yticks([])
plt.show()

输出结果：