总结

• ac4题，赛后补了E
• T1 计数
• T2 单源最短路dijikstra
• T3 多源最短路floyd
• 

A - Overall Winner

链接: A - Overall Winner

1. 题目描述

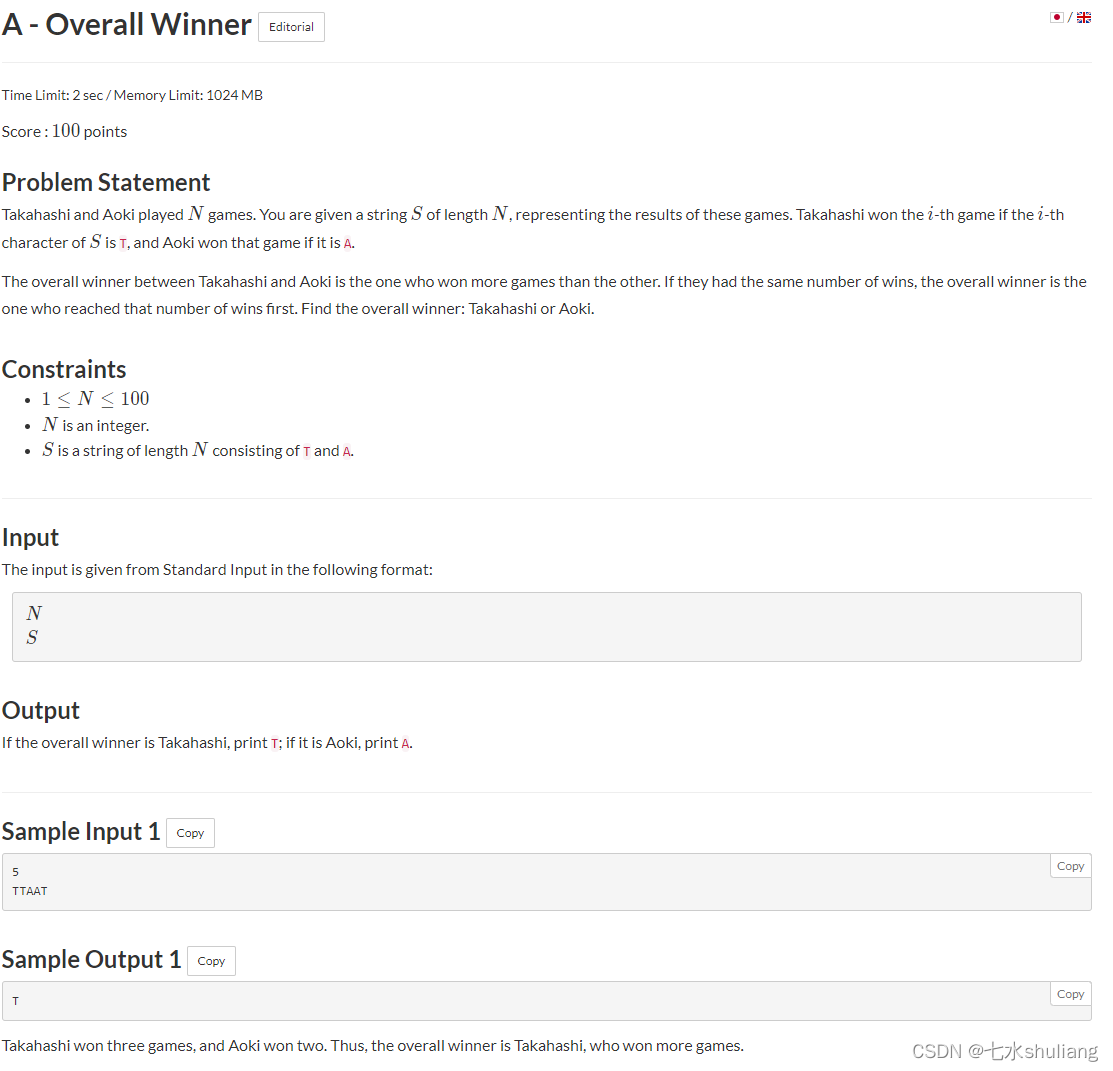
2. 思路分析

• 模拟

3. 代码实现

PROBLEM = """给一个只有A、T组成的字符串s，
谁多谁赢，一样多就从左到右看，谁先达到这个数。
"""
"""计数，一样多就看最后一个数是谁谁输"""

#       ms
def solve():
    n, = RI()
    s, = RS()
    cnt = Counter(s)
    # print(cnt)
    if cnt['T'] > cnt['A']:
        print('T')
    elif cnt['T'] < cnt['A']:
        print('A')
    else:
        if s[-1] == 'T':
            print('A')
        else:
            print('T')

B - Fill the Gaps

链接: B - Fill the Gaps

1. 题目描述

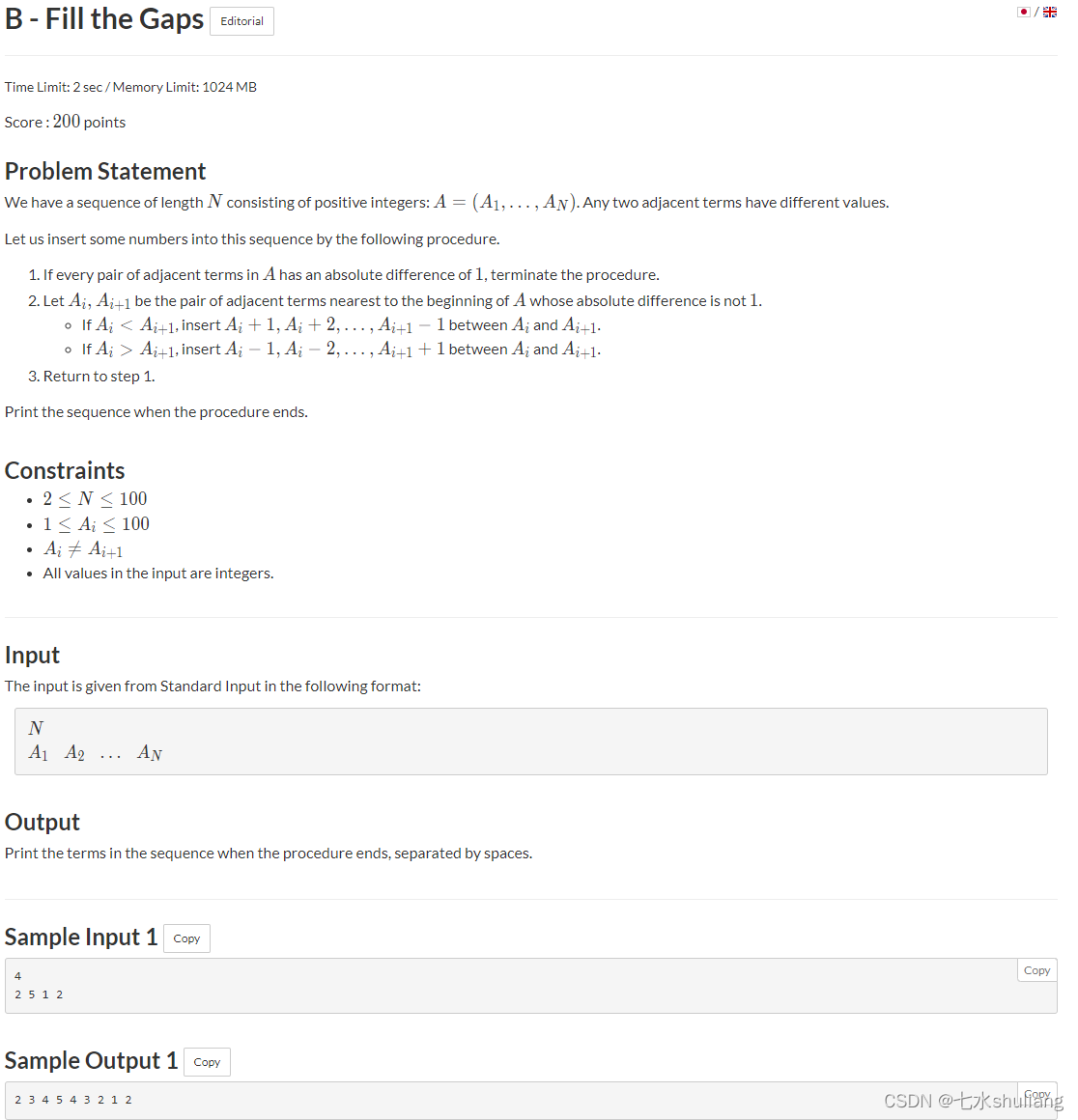
2. 思路分析

• 直接模拟。

3. 代码实现

PROBLEM = """给长为n的数组a，保证相邻的数不同。
在a中添加数，规则如下：
若a[i]<a[i+1]，添加a[i]+1,a[i]+2..a[i+1]-1.
若a[i]>a[i+1]，添加a[i]-1,a[i]-2..a[i+1]+1.
"""
"""直接模拟"""


#       ms
def solve():
    n, = RI()
    a = RILST()
    ans = [a[0]]
    for i in range(1, n):
        v = a[i]
        if ans[-1] < v:
            ans.extend(list(range(ans[-1] + 1, v)))
        else:
            ans.extend(list(range(v + 1, ans[-1]))[::-1])
        ans.append(v)
    print(*ans)

C - AtCoder Cards

链接: C - AtCoder Cards

1. 题目描述

2. 思路分析

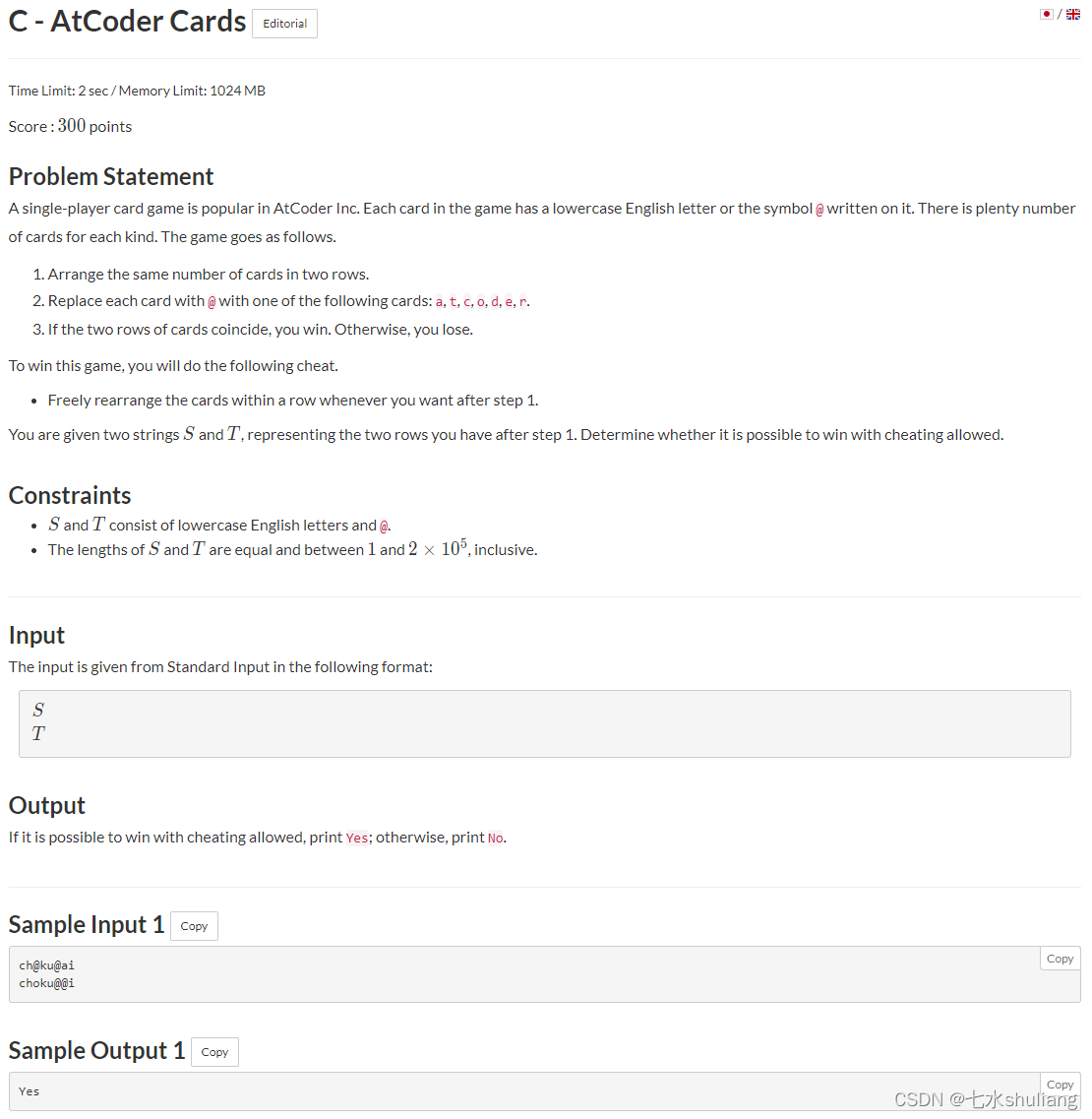
• 由于可以重排t，就是个普通的计数。wa2次不该。

3. 代码实现

PROBLEM = """给两个字符串s和t，只含小写字母和'@'。
其中'@'可以替换成任意'atcoder'几个字符中的一个。
开始前，你可以重排t。问是否能使s和t完全相同。
"""
"""计数每个字符，计算差异。最终看看差异的字符能否用对方行的'@'补回来即可。
"""

#       ms
def solve():
    s, = RS()
    t, = RS()
    cnt = Counter()
    x = y = 0
    for a, b in zip(s, t):
        if a == '@':
            x += 1
        else:
            cnt[a] += 1
        if b == '@':
            y += 1
        else:
            cnt[b] -= 1
    # print(cnt, x, y)
    for k, v in cnt.items():
        if v == 0:
            continue
        if k not in 'atcoder':
            return print('No')
        if v > 0 and y >= v:
            y -= v
        elif v < 0 and x >= -v:
            x += v
        else:
            return print('No')

    print('Yes')

D - Bitmask

链接: D - Bitmask

1. 题目描述

2. 思路分析

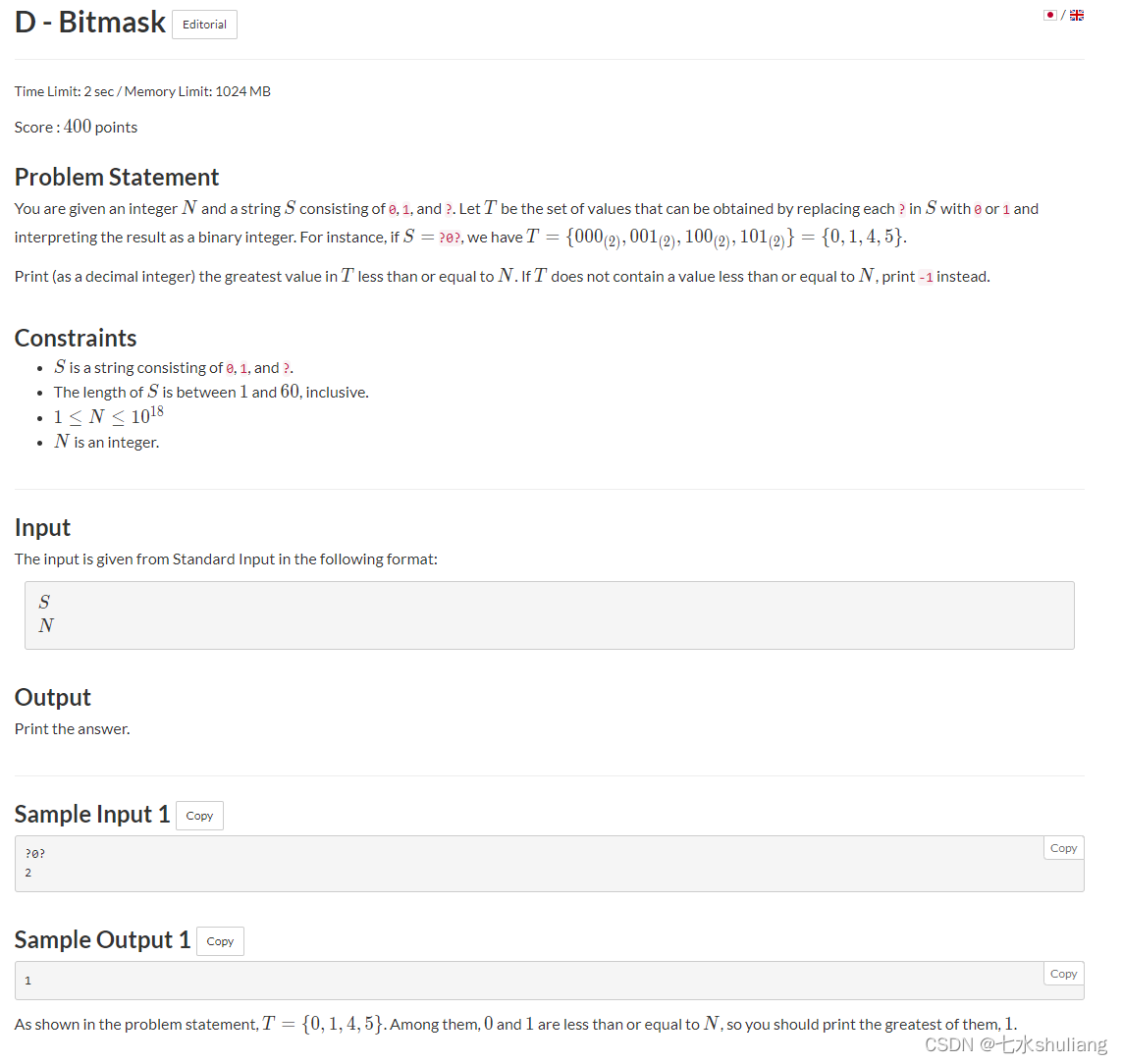
• 直接贪心比较好。

3. 代码实现

PROBLEM = """给一个只含'01?'的01字符串，你可以把'?'替换成0/1.
给一个数字n。问s能生成的最大数字x(x<=n)是多少。
"""
"""
- s长度超过n，且前边的位数有1是无法生成的，返回-1；否则可以都填0
- 后边对齐的位，前缀相同的情况下，出现n里0，s是1是非法的。否则一定可以生成。
类似数位dp的dfs即可，贪心的让每位优先取1再取0。
---
另外，可以直接贪：
先把所有1放到数字里，计算这些1是否已经>n，返回-1;
否则：
从高到低，对s里每个?，尝试放1，不行就放0.
"""

#       ms
def solve():
    s, = RS()
    n, = RI()
    p = bin(n)[2:]
    if len(s) < len(p):
        s = s.replace('?', '1')
        return print(int(s, 2))
    if len(s) >= len(p):
        d = len(s) - len(p)
        for i in range(d):
            if s[i] == '1':
                return print(-1)
        s = s[d:]

        for x, y in zip(s, p):
            if y == '1' and x in '?0':
                break
            if y == '0' and x == '1':
                return print(-1)

        ans = []

        def dfs(i, is_limit):
            if i == len(s):
                return True

            if s[i] != '?':
                if is_limit and s[i] > p[i]:
                    return False
                ans.append(s[i])
                if dfs(i + 1, is_limit and s[i] == p[i]):
                    return True
                ans.pop()
            else:
                if not is_limit or p[i] == '1':
                    ans.append('1')
                    if dfs(i + 1, is_limit and '1' == p[i]):
                        return True
                    ans.pop()
                ans.append('0')
                if dfs(i + 1, is_limit and '0' == p[i]):
                    return True
                ans.pop()
            return False

        if dfs(0, True):
            print(int(''.join(ans), 2))
        else:
            print(-1)

E - Pac-Takahashi

链接: E - Pac-Takahashi

1. 题目描述

2. 思路分析

• BFS+状压DP。学到了！

3. 代码实现

PROBLEM = """给两个字符串s和t，只含小写字母和'@'。
其中'@'可以替换成任意'atcoder'几个字符中的一个。
开始前，你可以重排t。问是否能使s和t完全相同。
"""
"""计数每个字符，计算差异。最终看看差异的字符能否用对方行的'@'补回来即可。
"""
PROBLEM = """给一个m行n列的矩阵，其中矩阵的每个位置：
'S' 代表起始位置
'G' 代表目标位置
'#' 代表墙
'.' 代表路
'o' 代表这个位置有糖果。题目保证最多有18个糖果。
1<=m,n<=300。
问在t步内，是否能到达终点。若能，最多能收集多少个糖果。
"""
"""据说是两个非常裸的典拼到一起。但第二个我真不会，这次算学学。
- 注意到糖果最多只有18个，考虑18次bfs/状态压缩。
- 然而这题这两步都要做。
- 容易想到，从起始位置尝试经过1个糖果，再去下一个糖果..最终到达目标位置。
- 这样就要先计算出每个糖果到彼此的距离，以及到终点的距离。
1. 把(所有糖果+起始位置)它们互相之间的距离都计算出来，这个可以算20次最短路。（朴素bfs即可，因为权是1.
2. 对这20个位置状压，进行一个状压DP
    - 定义:f[mask][j]代表在状态mask下，最终到达j点的最短步数。其中mask第i为是1代表去过i位置。
    - 转移:从小到大刷表，每次对mask的每一个1，尝试从这个1(第j位)到达一个不在mask中的位置k，则可以更新mask|k的状态为f[mask][j] + dis[j][k]
    - 初始:令第0位是起始，第1位是终点，那么f[1][0]=0,即访问过0位置，且在0位置需要的步数为0.
    - 答案:对每个状态，若它终点为1的步数<=t,则可以尝试这个方案，mask.bit_count()-2,因为有2个位置是起始结束。
"""


#       ms
def solve():
    m, n, t = RI()
    g = []
    cnt = 2
    cc = {}
    for i in range(m):
        s, = RS()
        g.append(s)
        for j, c in enumerate(s):
            if c == 'S':
                sx, sy = i, j
            elif c == 'G':
                gx, gy = i, j
            elif c == 'o':
                cc[(i, j)] = cnt
                cnt += 1
    cc[(sx, sy)] = 0
    cc[(gx, gy)] = 1
    dis = [[inf] * cnt for _ in range(cnt)]

    # print(1)
    def inside(x, y):
        return 0 <= x < m and 0 <= y < n and g[x][y] != '#'

    def bfs(x, y):
        u = cc[x, y]
        dist = [[10**9] * n for _ in range(m)]
        dist[x][y] = 0
        q = deque([(x, y)])
        while q:
            # print(q)
            x, y = q.popleft()
            d = dist[x][y]
            if (x, y) in cc:
                v = cc[x, y]
                dis[u][v] = d
            d += 1
            for dx, dy in DIRS:
                a, b = x + dx, y + dy
                if inside(a, b) and dist[a][b] > d :
                    dist[a][b] = d
                    q.append((a, b))

    for x, y in cc:
        bfs(x, y)
    if dis[0][1] > t:
        return print(-1)
    # print(dis)
    # 有cnt个点，给出他们分别到达彼此的距离，问从0最终到1的每种方案的最短距离。
    f = [[10 ** 9] * (1 << cnt) for _ in range(cnt)]  # f[i][j] 代表在状态i最后位置是j需的步数
    f[0][1] = 0  # 一开始站在位置0上，这个状态是1。
    for i in range(1 << cnt):
        for j in range(cnt):  # i状态里有j这个点，尝试从j出发
            if i >> j & 1:
                for k in range(cnt):
                    if i >> k & 1: continue  # k不在i里，那么从j到k
                    f[k][i | (1 << k)] = min(f[k][i | (1 << k)], f[j][i] + dis[j][k])
    ans = 0
    for i in range(1 << cnt):
        if f[1][i] <= t:
            ans = max(ans, bin(i).count('1')-2)
    print(ans)

六、参考链接

• 无